МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИК БЕЛАРУСЬ

УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«МИНСКИЙ ГОСУДАРСТВЕННЫЙ ВЫСШИЙ РАДИОТЕХНИЧЕСКИЙ КОЛЛЕДЖ»

кафедра общетехнических

дисциплин

КУРСОВАЯ РАБОТА

на тему: ЦИФРОВОЕ ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ

Исполнитель: студент 3 курса, 05181 группы

Шкуратович Тимофей Валерьевич

Научный руководитель: преподаватель доцент

Образцова Ольга Николаевна

Минск, 2013

Оглавление

Оглавление 2

Введение 3

Глава 1. Цифровое представление аналоговых сигналов 4

1. Операции, выполняемые над аналоговым

сигналом для его представления в цифровой форме 4

2. Теорема Котельникова 13

Выводы по 1-й главе 15

Глава 2. Устройства цифро-аналогового и

аналого-цифрового преобразования 16

2.1. Цифро-аналоговые преобразователи 16

2.2. Аналогово-цифровые преобразователи 22

Выводы по 2-ой главе 27

Заключение 28

Библиография 29

Введение

Современные информационно-вычислительные, измерительные и другие приборы могут работать как с аналоговыми, так и с цифровыми сигналами. Но всё более часто им требуется именно цифровое представление сигнала.

Целью исследования является выявление общих принципов преобразования сигналов, и практическая реализация этого процесса через конкретные приборы.

Гипотетически цифровой сигнал как способ передачи информации незаменим, ведь аналоговый сигнал можно зашифровать в гораздо меньший объём информации, что позволяет передавать по тому-же самому каналу (проводу) в десятки, а-то, и в сотни больше информации, даже с учётом того, что информация будет дублироваться для уменьшения количества помех.

В этой работе я ставлю перед собой задачу близко рассмотреть преобразование аналогового сигнала в цифровой, связь этого преобразования с теоремой Котельникова, а так-же изучить некоторые аналогово-цифровые и цифро-аналоговые преобразователи.

Глава 1. Цифровое представление аналоговых сигналов

1. Операции, выполняемые над аналоговым сигналом для его представления в цифровой форме

Аналоговый сигнал — (рис. 1.1.) сигнал данных, у которого каждый из представляющих параметров описывается функцией времени и непрерывным множеством возможных значений.

Аналоговые сигналы описываются непрерывными функциями времени, поэтому аналоговый сигнал иногда называют непрерывным сигналом. Аналоговым сигналам противопоставляются дискретные (квантованные, цифровые).

Рисунок 1.1. – Аналоговый сигнал

Свойства аналоговых сигналов в значительной мере являются противоположностью свойств квантованных или цифровых сигналов.

Отсутствие чётко отличимых друг от друга дискретных уровней сигнала приводит к невозможности применить для его описания понятие информации в том виде, как она понимается в цифровых технологиях. Содержащееся в одном отсчёте «количество информации» будет ограничено лишь динамическим диапазоном средства измерения.

Отсутствие избыточности. Из непрерывности пространства значений следует, что любая помеха, внесенная в сигнал, неотличима от самого сигнала и, следовательно, исходная амплитуда не может быть восстановлена. В действительности фильтрация возможна, например, частотными методами, если известна какая-либо дополнительная информация о свойствах этого сигнала (в частности, полоса частот).

Аналоговые сигналы часто используют для представления непрерывно изменяющихся физических величин. Например, электрического напряжения.

Для преобразования аналогового сигнала в цифровой необходимо провести три действия над исходным аналоговым сигналом:

• Дискретизация сигнала по времени

• Квантование сигнала по уровню

• Кодирование сигнала

Частота дискретизации выбирается из теоремы Котельникова. В ней утверждается, что для того что бы по отсчётам сигнала можно было бы сколь угодно точно восстановить непрерывный сигнал необходимо что бы частота дискретизации не менее чем в два раза превосходила верхнюю частоту спектра дискретизируемого сигнала.

Любой сигнал имеет своё спектральное представление. Любое представление сигнала – это представление в виде суммы (или интеграла) гармонических составляющих (синусоид и косинусоид), различных частот взятых с определёнными весовыми коэффициентами (имеющими определённую амплитуду)

Для периодических сигналов это сумма, для непериодический – интеграл.

Переход к спектру сигнала осуществляется с помощью прямого преобразования Фурье.

Рассмотрим переход к спектральному представлению в виде периодической функции:

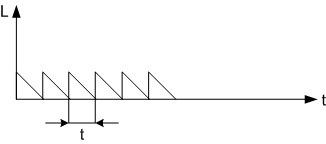
Рисунок 1.2. – Периодический сигнал

Как известно периодическая функция удовлетворяющая условию Дирихле может быть представлена рядом гармонических функций.

По формуле Эйлера любое выражение можно представить в виде

— частота первой гармоники

— частота n-ой гармоники

— круговая частота n-ой гармоники

— комплексная амплитуда гармоники, где — фазовый спектр.

Совокупность амплитуд гармоник ряда Фурье называется амплитудным спектром, а совокупность их фаз называется фазовым спектром.

Пример спектра:

Рисунок 1.3. – Спектр сигнала

Для непериодический функции , а тогда заменяется непрерывно изменяющейся частотой => сумма заменяется интегралом.

Прямое преобразование Фурье для непериодического сигнала

Рисунок 1.4. – Квантование сигнала по уровню

Количество уровней квантования определяется по формуле

n — количество разрядов

N — уровень квантования

Выбор количества уровней квантования сигналов производится на основе компромиссного подхода, учитывающего с одной стороны необходимость достаточно точного представления сигнала, что требует большого числа уровней квантования, а с другой стороны количество уровней квантования должно быть меньше, что бы разрядность кода была минимальной.

Таким образом спектр непериодической функции представляется суммой бесконечного количества гармонических колебаний, частоты которых расположены бесконечно близко друг к другу.

Кодирование

Процесс кодирования при формировании цифровых сигналов заключается в замене значения амплитуды каждого дискретного квантованного отсчета кодовой комбинацией двоичного кода. Причем кодируется не абсолютное значение амплитуды, а номер уровня квантования, которому соответствует данная амплитуда. Важной характеристикой кодера при этом является разрядность кодовой комбинации (n), под которой понимают количество элементов используемых в одной кодовой комбинации. Разрядность кодовой комбинации зависит от количества уровней квантования и определяется для равномерного двоичного кода как

n = log₂L_кв

При заданной разрядности L_кв определяется из выражением

L_кв = 2n

Таким образом, важными характеристиками при преобразовании аналогового сигнала в цифровой являются:

- шаг дискретизации;

- шаг квантования;

- разрядность кодовой комбинации.

Процесс формирования цифрового сигнала представлен на рисунке

Рисунок 1.5. – Формирование цифрового сигнала:

а) аналоговый сигнал; б) дискретизация; в) квантованный сигнал;

г) ошибка квантования; д) цифровой сигнал

Дискретный сигнал – (разделённый, прерывистый) сигнал представленный в виде последовательности значений, взятых в дискретные моменты времени, с определённой частотой дискретизации.

Частота дискретизации – частота взятия отсчетов непрерывного во времени сигнала при его дискретизации (в частности, аналого-цифровым преобразователем). Измеряется в герцах.

Чем выше частота дискретизации, тем более широкий спектр сигнала может быть представлен в дискретном сигнале. Как следует из теоремы Котельникова, для того, чтобы однозначно восстановить исходный сигнал, частота дискретизации должна более чем в два раза превышать наибольшую частоту в спектре сигнала.

Дискретизация – преобразование непрерывной функции в дискретную.

Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени. Эти значения называются отсчётами. Δt называется интервалом дискретизации.

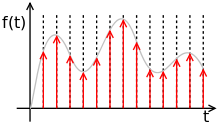
Рисунок 1.6. – Дискретный сигнал

Квантование – в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей. Простейшим видом квантования является деление целочисленного значения на натуральное число, называемое коэффициентом квантования.

При квантовании вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности. Расстояния между этими уровнями называется шагом квантования Δ. Число этих уровней равно N (от 0 до N-1). Каждому уровню присваивается некоторое число. Отсчёты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования. Каждый уровень квантования кодируется двоичным числом с n разрядами. Число уровней квантования N и число разрядов n двоичных чисел, кодирующих эти уровни, связаны соотношением n ≥ log2(N).

Рисунок 1.7. – Квантованный сигнал

Не следует путать квантование с дискретизацией (и, соответственно, шаг квантования с частотой дискретизации). При дискретизации изменяющаяся во времени величина (сигнал) замеряется с заданной частотой (частотой дискретизации), таким образом, дискретизация разбивает сигнал по временной составляющей (на графике — по горизонтали). Квантование же приводит сигнал к заданным значениям, то есть, разбивает по уровню сигнала (на графике — по вертикали). Сигнал, к которому применены дискретизация и квантование, называется цифровым.

Квантование часто используется при обработке сигналов, в том числе при сжатии звука и изображений.

При оцифровке сигнала уровень квантования называют также глубиной дискретизации или битностью. Глубина дискретизации измеряется в битах и обозначает количество бит, выражающих амплитуду сигнала. Чем больше глубина дискретизации, тем точнее цифровой сигнал соответствует аналоговому. В случае однородного квантования глубину дискретизации называют также динамическим диапазоном и измеряют в децибелах (1 бит ≈ 6 дБ).

Виды квантования

Однородное (линейное) квантование — разбиение диапазона значений на отрезки равной длины. Его можно представлять как деление исходного значения на постоянную величину (шаг квантования) и взятие целой части от частного: .

Квантование по уровню — представление величины отсчётов цифровыми сигналами. Для квантования в двоичном коде диапазон напряжения сигнала от U_min до U_max делится на 2ⁿ интервалов. Величина получившегося интервала (шага квантования):

Каждому интервалу присваивается n-разрядный двоичный код — номер интервала, записанный двоичным числом. Каждому отсчёту сигнала присваивается код того интервала, в который попадает значение напряжения этого отсчёта. Таким образом, аналоговый сигнал представляется последовательностью двоичных чисел, соответствующих величине сигнала в определённые моменты времени, то есть цифровым сигналом. При этом каждое двоичное число представляется последовательностью импульсов высокого (1) и низкого (0) уровня.

Цифровой сигнал — сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.

Сигналы представляют собой дискретные электрические или световые импульсы. При таком способе вся емкость коммуникационного канала используется для передачи одного сигнала. Цифровой сигнал использует всю полосу пропускания кабеля. Полоса пропускания — это разница между максимальной и минимальной частотой, которая может быть передана по кабелю. Каждое устройство в таких сетях посылает данные в обоих направлениях, а некоторые могут одновременно принимать и передавать. Узкополосные системы (baseband) передают данные в виде цифрового сигнала одной частоты.

Рисунок 1.8. – Цифровой сигнал

Дискретный цифровой сигнал сложнее передавать на большие расстояния, чем аналоговый сигнал, поэтому его предварительно модулируют на стороне передатчика, и демодулируют на стороне приёмника информации. Использование в цифровых системах алгоритмов проверки и восстановления цифровой информации позволяет существенно увеличить надёжность передачи информации.

Замечание. Следует иметь в виду, что реальный цифровой сигнал по своей физической природе является аналоговым. Из-за шумов и изменения параметров линий передачи он имеет флуктуации по амплитуде, фазе/частоте (джиттер), поляризации. Но этот аналоговый сигнал (импульсный и дискретный) наделяется свойствами числа. В результате для его обработки становится возможным использование численных методов (компьютерная обработка).

Важным свойством цифрового сигнала, определившего его доминирование в современных системах связи, является его способность к полной регенерации вплоть до некоторого порогового отношения сигнал/шум, в то время как аналоговый сигнал удаётся лишь усилить вместе с наложившимися на него шумами. Здесь же кроется и недостаток цифрового сигнала: если цифровой сигнал утопает в шумах, восстановить его невозможно (эффект крутой скалы (англ.)), в то время как человек (не машина) может усвоить информацию из сильно зашумлённого сигнала на аналоговом радиоприёмнике, хотя и с трудом. Если сравнивать сотовую связь аналогового формата (AMPS, NMT) с цифровой связью (GSM, CDMA), то при помехах на цифровой линии из разговора выпадают порой целые слова, а на аналоговой можно вести разговор, хотя и с помехами. Выход из данной ситуации - почаще регенерировать цифровой сигнал, вставляя регенераторы в разрыв линии связи, или уменьшать длину линии связи (например, уменьшать расстояние от сотового телефона до базовой станции (БС), что достигается более частым расположением БС на местности).