Вопрос 33.
Экстремумы функции. Необходимое и достаточное условие экстремума функции.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Теорема.(Необходимое условие экстремума). Если функция y =f(x) в точке х0 имеет экстремум, то производная f/( x 0 ) равна нулю.
Теорема(Достаточное условие экстремума).
Пусть функция f(x) непрерывна на отрезке [a , b], а точка x0 из этого отрезка является критической.
Вопрос 34.Асимптоты функций. Нахождение вертикальны, наклонных и горизонт асимптот функций.
Асимптотой функции называют прямую, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
Вертикальные асимптоты
Вертикальные асимптоты определяются точками разрыва функции и границами области определения. График функции, непрерывной на всей числовой прямой, вертикальных асимптот не имеет. Некоторые особенности поведения функции в окрестности вертикальных асимптот представлено на рисунке. Вертикальные асимптоты определяются точками разрыва второго рода В этом случае f( x0 ± 0) = ± ∞, или f ( x0 ± 0) = + ∞ , или f (x0 ± 0) = − ∞. Следует отметить, что в этом случае может отмечаться всё разнообразие поведения функции в окрестности точки разрыва. Например, на рис. 8.2 приведён график элементарной функции
.
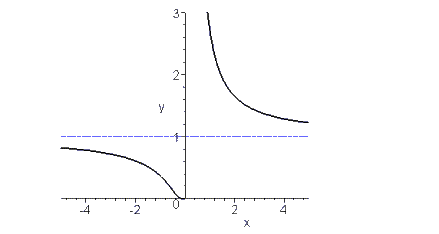Рис.
8.2. Точка разрыва второго рода для данной
функции определяется только справа
Горизонтальные асимптоты
Если
,
то у = b — горизонтальная асимптота кривой y = f (x) (правая – при х стремящемуся к плюс бесконечности, левая – при х стремящемуся к минус бесконечности и двусторонняя, если пределы при х стремящемуся к плюс-минус бесконечности равны).
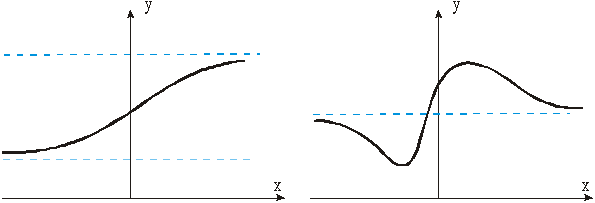Рис.
8.3. Примеры горизонтальных двухсторонних
и односторонних асимптот
Уравнение наклонной асимптоты функции y = f (x) определим уравнением y =k·x + b. При этом параметры наклонной асимптоты определяются соотношениями
,
.
Для того, чтобы функция y = f (x ) имела асимптоту y = k ·x + b, необходимо и достаточно, чтобы существовали указанные выше конечные пределы.
Доказательство. По определению асимптоты имеем
.
Так как MP = MP1·cos α, где угол α есть величина постоянная, равная углу наклона асимптоты к оси Ох. Поэтому соотношение для определения асимптоты можно записать в виде
.
Так как точки М и Р1 соответствуют одному и тому же значению аргумента, то это соотношение можно записать в виде
. (9.1)
Если вынести за скобки х, то
,
из этого однозначно будет следовать
,
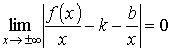или
.
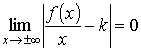Откуда следует соотношение для нахождения углового коэффициента асимптоты
.
Зная угловой коэффициент асимптоты, из соотношения (9.1) получим
.
36. Определители и их основные св-ва.
Определителем называется число, записанное в виде квадратной таблицы:
.
Таблица
ограничивается слева и справа
вертикальными линиями, 
-называется
элементами определителя ( 
-номер
строки, 
-номер
столбца).
Главная
диагональ определителя содержит
элементы 
,
противоположная диагональ называется
побочной.
Порядком определителя называется число строк (столбцов) квадратной таблицы.
Определитель II порядка вычисляется по формуле:
Определитель III порядка можно вычислить по правилу Сарруса:
Основные свойства определителей:
1.1. Значение определителя не изменится, если:
- строки заменить на столбцы, такое действие называется транспонирование, т.е. действия, выполняемые со строками, справедливы и для столбцов;
- все элементы одной строки умножить на какое-либо число и прибавить к соответствующим элементам другой строки.
Такие действия с элементами определителя называются элементарными преобразованиями.
1.2. Определитель меняет знак на противоположный, если две каких-либо строки поменять местами.
1.3. Определитель равен нулю, если:
- все элементы какой-либо строки равны нулю;
- соответствующие элементы каких-либо двух строк равны;
- соответствующие элементы каких-либо двух строк пропорциональны.