18.Класификация точек разрыва ф-ции.

Если в точке х0 условие непрерывности нарушается, то говорят, что функция в точке х0 терпит разрыв/имеет точку разрыва.

Условие непрерывности: предел справа существует и конечен, предел слева существует и конечен, они равны между собой и равны значению функции в точке.

Точка х0 называется точкой разрыва первого рода, если в этой точке существуют конечные пределы функции справа и слева, но не равны значению функции; если эти пределы равны, то разрыв называется устранимым.

Точка х0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует или бесконечен.

19. Производная. Геометрический смысл производной.

Понятие производной

Рассмотрим функцию y=f(x) на интервале (a;b). Возьмём на этом интервале точку х0 и приращение на оси Ох. Прямая, соединяющая 2 точки (х0;f(x0)) и (x0+x;f(x0+x))на графике функции называется секущей.

У гловой коэффициент секущей равен отношению приращения функции к вызвавшему его приращению аргумента.

П роизводной функции y=f(x) называется предел отношения приращения функции к вызвавшему его приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует)

Если предел конечен, то производная конечная, если предел бесконечен, то производная бесконечна.

Геометрический смысл производной

прямая y-y0=k(x-x0), угловой коэффициент которой равен производной функции в данной точке (k=f’(x0)) называется касательной к графику функции в данной точке.

При х0, значение х0+хх0, т.е. секущая стремиться занять положение касательной, так будем говорить, что касательная есть предельное положение секущей.

Геометрический смысл производной состоит в том, что она равна tg угла наклона касательной.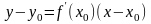

П рямая, перпендикулярная касательной в точке касания называется нормалью

.

-уравнение нормали в точке х0.

Вопрос 20. Теорема о связи фифференцируемости и непрерывности функции в точке. Теорема 2 (дифференцируемость и непрерывность). Если  функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_ x 0 y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называетсякусочно гладкой.

Вопрос 21. Производные основных элементарных функций.

Производные тригонометрических функций.

Производная от y=sinx, это y’=cosx. Дадим аргументу x приращение ∆x; тогда 1) y+∆y=sin(x+∆x); 2) ∆y=sin(x+∆x)-sinx=2sin ;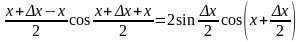

3) 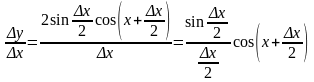; 4) 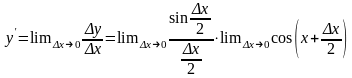, но так как 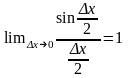, то 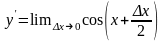=cosx. Последнее равенство получается на том основании, что cosx есть непрерывная функция. Так же y=cosx y’=-sinx. Производная от y=tgx, равна 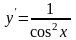. По правилу дифференцирования дроби получаем: 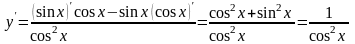. Так же y=ctgx, равен .

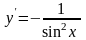. Производная степенной и показательной функций.

Производная от (показательная функция) функции a^x, где а > 0, равна a^xlna, т.е. y=a^x, равна y’=a^xlna. Логарифмируя равенство y=a^x, получим: lny=xlna или y’=a^xlna. Если оснавание а=е, то lne=1 и мы получим y=e^x, y’=e^x. Производная от (степенная функция) xⁿ, где n – любое действительное число, равна nx^n-1. Пусть x > 0. Логарифмируя данную функцию, будем иметь: lny=nlnx. Дифференцируем обе части полученного равенства по х, считая у функцией от х: 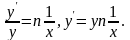Подставляя сюда значение y=xⁿ, окончательно получаем: y’=nx^n-1. Эта формула верна и для x < 0, если только xⁿ имеет смысл.

Производная логарифмической функции. Логарифмическое дифференцирование, производная степенно-показательной функции.

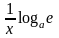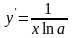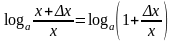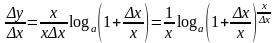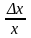Производная от log_ax, равна или . Если ∆y есть приращение функции y=log_ax, соответствующее приращению ∆x аргумента x, то y+∆y=log_a(x+∆x); ∆y=log_a(x+∆x)-log_ax= . Помножим и разделим на x выражение, состоящее в правой части последнего равенства . Обозначим величину через α. Очевидно, 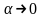при 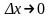и данном x. Следовательно, 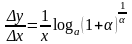, но как известно 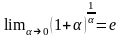. Если же выражение, стоящее под знаком логарифма, стремится к числе e, то логарифм этого выражения стремится к log_ae (в силу непрерывности логарифмической функции). Поэтому окончательно получаем: 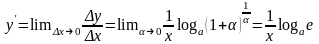. Заметив, что 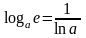, полученную формулу можно переписать так: .

Производные обратных тригонометрических функций.

1)Рассмотрим ф-цию y=arcsinx;-1≤x≤1.Обратной этой ф-ции явл. x=siny (-π/2≤y≤π/2) Причём производная обратной ф-ции сущ. x’(y)=cosy;≠0;для любого у из(-π/2;π/2) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=1/cosy=1/cos(arcsinx)=1/√(1-sin²(arcsinx))=1/√(1-x²) (arcsinx)’=1/√(1-x²) Аналогично (arccosx)’= -1/√(1-x²) xε(-1;1) 2)y=arctgx x xε(-∞;∞)Обратная x=tgy -π/2≤y≤π/2 Производная обратной ф-ции сущ. x’(y)=1/cos²y≠0 для любого у ε(-π/2;π/2) ) =>по теореме о дифф. Обратной ф-ции имеем y’(x)=1/x’(y)=cos²y=cos²(arctgx)=1/1+tg²(arctgx)=1/1+x² (arctgx)’=1/1+x² xε(-∞;∞) Аналогично (arсctgx)’= -1/1+x²) (с графиками).

.Гиперболические ф-ции и их производные.

Ф-ция y=e^x-не явл. ни чётной,ни нечётной,но её можно представить в виде суммы двух слагаемых из которых одно:чётная ,второе-нечётная ф-ция e^x=(e^x+e^-x)/2+(e^x-e^-x)/2

(e^x+e^-x)/2=chx-гиперболический cos (чётная)

(e^x-e^-x)/2=shx-гиперболический sin(нечётная)shx/chx=thx

chx/shx=cthx

Св-ва гиперболических ф-ций напоминают св-ва тритгонометрпических ф-ций

ch²x-sh²x=1; ch²x+sh²x=ch2x; 2shx *chx=sh2x

Найдём произв.от тригонометрич.ф-ций: (shx)’=chx; (chx)’=shx ;thx=1/ch²x;

(cthx)’= -1/sh²x

Производные неявных и параметрических ф-ций.

Неявн.Пусть знач.x и y связаны некоторым ур-ем F(x;y)=0(1)Если ф-ция y=f(x)определена на интервале(ab),такова что ур-е(1)при подстановке в него вместо y выраж.f(x)обращается в ождество относительно x,то ф-ция y=f(x)есть неявная ф-ция,определёная ур-ем(1) Но не всякую неявно заданную ф-цию можно представить явно.Например y-x-siny=0

не всякую явно заданную ф-цию можно представить неявно При вычисл.знач. произв.неявной ф-ции при данном знач.ар-та,нужно знать ещё и знач.ф-ции y,при данном знач.аргумента Парам. {x=α(t); y=λ(t)(1)T1≤t≤T2 Каждому значению t соответствуют значения x и y.Если рассматривать x и y как координаты точки на плоскости XOY,то каждому значению t будет соответствовать определённая точка на плоскости.Когда t изменяется от T1 до Т2,то эта точка на пл-ти описывает некоторую кривую.Ур-я(1)называются параметр.ур-ями этой кривой,t параметром.А способ задания кривой ур-ями(1)называется параметрическим. Пусть ф-ция x=α(t)имеет обратную t=Ф(x),тогда y явл.сложной ф-цией от x.y=α[Ф(х)]Таким образом ур-я (1)определяют у как ф-цию от х , и говорят что эта ф-ция у(х)задана параметр. Найдём произв.ф-ции заданой ур-ями (1).Предположим ,что α(t),λ(t)имеют произв.,кроме того ф-ция х=λ(t),имеет обратную t=Ф(х),которая также имеет производную,тогда ф-цию у=f(x)можно рассматр. Как сложную ф-цию у=λ[Ф(х)] ,t=Ф(х)-промежуточный аргумент y'(x)=y’(t) *t’(x)по правилу дифф. Обратной ф-ции.y’(x)=y’(t)/x’(t) или y’(x)=λ’(t)/α’(t).

Вопрос 22. Теорема о вынесении константы за знак производной и о производной суммы двух функций.. ТЕОРЕМА 2. Константу можно вынести за знак производной, то есть

ТЕОРЕМА 3. Производная суммы любого числа функций равна сумме производных этих функций. Для трех функций, например, имеем:

Вопрос 23. Теорема о производной произведения

Производная произведения двух функций равна

Вопрос 24. Теорема о производной частного.

ТЕОРЕМА 5. Производная частного двух функций равна

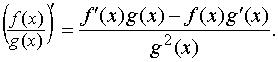
Вопрос 25. Производная сложной функции. Сложная функция – это функция, аргументом которой также является функция.

С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать какf(g(x)). То есть, g(x) как бы аргумент функции f(g(x)).

К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а   - целая рациональная функция (смотритеклассификацию элементарных функций), тогда  .

В свою очередь, g(x) также может быть сложной функцией. Например, 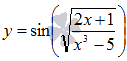 . Условно такое выражение можно обозначить как  . Здесь f – функция синуса,   - функция извлечения квадратного корня,   - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом  .

Часто можно слышать, что сложную функцию называют композицией функций.

Формула нахождения производной сложной функции.

Пример.

Найти производную сложной функции  .

Решение.

В данном примере f – функция возведения в квадрат, а g(x) = 2x+1 – линейная функция.

Вот подробное решение с использованием формулы производной сложной функции:

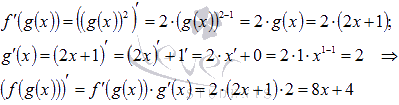
Давайте найдем эту производную, предварительно упростив вид исходной функции.

Следовательно,

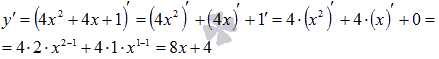
Как видите, результаты совпадают.