Вопрос 9-10. Теоремы о пределах суммы, произведения, частного двух функций. Первый и второй замечательные пределы. Примеры вычисления.

Теоремы:

1)Предел суммы двух функций равен сумме их пределов: .

Доказательство:

Пусть  , . Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать:   и  . Следовательно,  , где   - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать  , или  .

2)Предел произведения двух функций равен произведению их пределов: .

Доказательство:

Пусть  , . Тогда   и  . Следовательно

,

.

Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда  , т.е.  .

2)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен: .

Доказательство:

Пусть  , . Тогда   и  . Тогда  . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.

Поэтому  , т.е. 

Первый и второй замечательные пределы:

1)Первый замечательный предел: 

Пример вычисления:

.

2)Второй замечательный предел: 

Пример вычисления:

Вычислим  . Пусть  . Тогда:  .

Вопрос 11. Теорема о пределе промежуточной функции:Если функция ƒ(х) заключена между двумя функциями φ(х) и g(х), стремящимися к одному и тому же пределу, то она также стремится к этому пределу.

Формулировка

Пусть в некоторой окрестности   точки   функция   заключена между двумя функциями   и  , имеющими одинаковый предел   при  , то есть

Тогда  .

Доказательство

Из неравенства   получаем неравенство  . Тогда верно неравенство  . Условие   позволяет предположить, что для любого   существует окрестность  , в которой верны неравенства   и  . Из изложенной выше оценки максимумом следует, что   при  , что удовлетворяет определению предела, то есть  .

13 Первый замечательный предел.

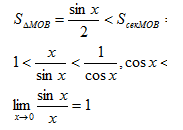. Док-во: возьмём единичную окружность. Угол МОВ=х 0<x</2. площадь треугольника МОВ меньше, чем площадь сектора МОВ и меньше, чем площадь треугольника СОВ. |MA|=sin x, |CB|=tgx.

по теореме о сжатой переменной.

14 Второй замечательный предел.

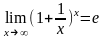
15 Различные формы записи 2 з.п.

16 Различные определения непрерывности ф-ции

Р азность Δx = x - x₀ называется приращением аргумента х в точке x₀, разность Δy = f (x) − f (x₀) называется приращением функции в точке х₀, вызванным приращением аргумента Δх. При фиксированной точке х₀ величина Δу является функцией аргумента Δ х. Равенство (5.2) в новых обозначениях принимает вид.

17 Односторонние пределы. Связь односторонних пределов с пределом ф-ции.

 Число А называется левым пределом функции f (x) в точке х₀, если для любого как угодно малого положительного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента меньших чем х₀ и отличающихся от него на величину меньшую δ, значения функции

отличаются от числа А на величину, меньшую чем ε:

Ч исло B называется правым пределом функции f (x) в точке х₀, если для любого как угодно малого положительного числа ε можно найти зависящее от этого ε положительное число δ, что для всех значений аргумента больших, чем х₀ и отличающихся от него на величину меньшую чем δ, значения функции отличаются от числа В на величину, меньшую чем ε:

Предел ф-ции в точке.