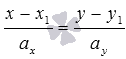49. Угол между двумя прямыми на плоскости.

Угол между двумя прямыми равен углу между их направляющими векторами.

Если прямые заданы следующими уравнениями:

A₁x + B₁y + C₁ = 0 и A₂x + B₂y + C₂ = 0

тогда направляющие векторы этих прямых будут равны:

a₁ = (- B₁ ; A₁) и a₂ = (- B₂ ; A₂)

Воспользуемся вормулой скалярного произведения двух векторов:

из этой формулы получим:

Выразим угол φ :

Из последней формулы получим:

Вопрос50 Уравнение плоскости, проходящей через три заданные точки

 Пусть плоскость проходит через точки   и  , не лежащие на одной прямой и   – произвольная точка плоскости. Тогда векторы  ,

  ,   компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

.

 

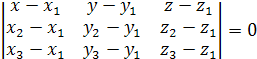Это уравнение, которому удовлетворяют координаты   любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

51. Общее уравнение плоскости и его исследование.

Всякое уравнение вида  , где A, B, C и D – некоторые действительные числа, причем А, В и C одновременно не равны нулю, определяет плоскость в заданной прямоугольной системе координат Oxyz в трехмерном пространстве, и всякая плоскость в прямоугольной системе координат Oxyz в трехмерном пространстве определяется уравнением вида   при некотором наборе чисел A, B, C и D.

Уравнение   называется общим уравнением плоскости в прямоугольной системе координат Oxyz в трехмерном пространстве.

Общее уравнение плоскости вида  , где   - некоторое действительное число, отличное от нуля, определяет в прямоугольной системе координатOxyz плоскость, совпадающую с плоскостью  , так как задает то же самое множество точек трехмерного пространства. К примеру, уравнения   и   задают одну и ту же плоскость, так как им удовлетворяют координаты одних и тех же точек трехмерного пространства.

52. Угол между двумя плоскостями

Угол между двумя плоскостями равен углу между их нормальными векторами. Пусть две пересекающиеся плоскости A₁x + B₁y + C₁z + D₁ = 0 и A₂y + B₂y + C₂z + D₂ = 0 имеют нормальные векторы  =(A₁;B₁; C₁) и  =(A₂; B₂; C₂). Тогда угол между этими плоскостями вычисляется по формуле: 

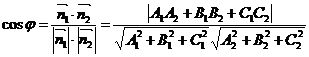
Для того чтобы две плоскости были параллельны, их нормальные векторы   и   должны быть коллинеарны, т.е.  , где λ≠0. Если ни одна из координат векторов   и   не равна нулю, то из последнего равенства следует, что: 

A₁ / A₂ = B₁ / B₂ = C₁ / C₂,

т.е. коэффициенты при соответствующих координатах пропорциональны.

Для того чтобы плоскости были перпендикулярны, их нормальные векторы   и   также должны быть перпендикулярны, т.е. их скалярное произведение равно нулю:  . Отсюда следует, что: 

A₁A₂ + B₁B₂ + C₁C₂ = 0.

53.Расстояние от точки до плоскости.

Расстояние от точки до плоскости равно длине перепендикуляра, опущенного из этой точки на плоскость.

54.Параметрические и канонические уравнения прямой линии в пространстве.

Пусть прямая проходит через точку   параллельно вектору  . Так как любой ненулевой вектор, параллельный данной прямой, является ее направляющим вектором, то для любой точки  , лежащей на данной прямой, вектор   коллинеарен направляющему вектору  . Поэтому их соответствующие координаты должны быть пропорциональны, следовательно, имеют место равенства:

,

Пусть прямая проходит через точку  , лежащую на прямой параллельно вектору  . Рассмотрим произвольную точку   на прямой. Очевидно, что  . Так как векторы   и   коллинеарны, то найдется такое число  , что  , причем число   может принимать любое числовое значение в зависимости от положения точки   на прямой. Множитель   называется параметром. Обозначив радиус-векторы точек   и   соответственно через   и  , получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра   соответствует радиус-вектор некоторой точки  , лежащей на прямой.

Так как векторы       то

.

 

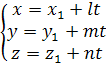Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра   изменяются координаты  и   и точка   перемещается по прямой.

55. Прямая как пересечение двух плоскостей. Переход к параметрическим (каноническим) уравнениям прямой.

Каждая прямая, если мы говорим о пространстве, включается в плоскость, при чем не одну, а в бесконечное множество. А если рассмотреть две плоскости, то они пересекаясь задают определенную прямую. Таким образом, мы можем рассматривая уравнения любых пересекающихся плоскостей, определить уравнение прямой, полученной на их пересечении. То есть, если есть плоскости заданные следующими уравнениями: Аа*х+Ва*у+Са*z+Dа=0 и Аb*х+Вb*у+Сb*z+Db=0, то система этих двух уравнений (объединяем на письме фигурной скобкой слева) определяет прямую на их пересечении. А сами уравнения имеют названия общих уравнений прямой.

Параметрическим уравнениям прямой на плоскости вида   соответствуетканоническое уравнение прямой на плоскости вида