
- •Тема: Нелинейные модели регрессии и линеаризация.
- •Некоторые виды нелинейных зависимостей, поддающиеся непосредственной линеаризации
- •Зависимость гиперболического типа
- •Показательная (экспоненциальная) зависимость
- •Зависисмость степенного типа
- •Зависимость логарифмического типа
- •Подбор линеаризующего преобразования: подход Бокса-Кокса.
- •Производственные функции
- •Свойства двухфакторной производственной функции
Производственные функции
Важную роль играют зависимости степенного типа в задачах построения и анализа производственных функций.
Производственная функция – экономико-математическая модель, позволяющая аппроксимировать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.
В качестве факторов ПФ могут выступать следующие переменные:
Объем выпущенной продукции;
Объем основного капитала или основных фондов;
Объем трудовых ресурсов или трудовых затрат.
Простой разновидностью ПФ являются однофакторные производственные функции (ОПФ). Зависимой переменной в данных функциях является объем производства , который зависит от единственной независимой переменной - ресурсы.
Двухфакторные производственные функции (ДПФ) характеризуют зависимость объема производства от каких-либо факторов. Чаще всего это факторы объема основного капитала и трудовых ресурсов. К наиболее известным двухфакторным ПФ относятся функции Кобба-Дугласа.
![]() ,
,
![]()
- объем выпуска продукции
![]() - объем основного
капитала
- объем основного
капитала
![]() = затраты живого
труда
= затраты живого
труда
Полученную степенную модель легко свести к линейной путем логарифмирования обеих частей:
![]()
Если сумма показателей степени в ПФ Кобба-Дугласа равна 1, то ее можно записать в следующей форме:
![]()
Таким образом,
зависимость производительности труда
![]() от его капиталовооруженности
от его капиталовооруженности
![]() .
.
Функция Кобба-Дугласа с учетом технического прогресса имеет вид:
![]() ,
где
,
где
![]() - время,
- время,
![]() - темп прироста объема производства
благодаря техническому прогрессу.
- темп прироста объема производства
благодаря техническому прогрессу.
Свойства двухфакторной производственной функции
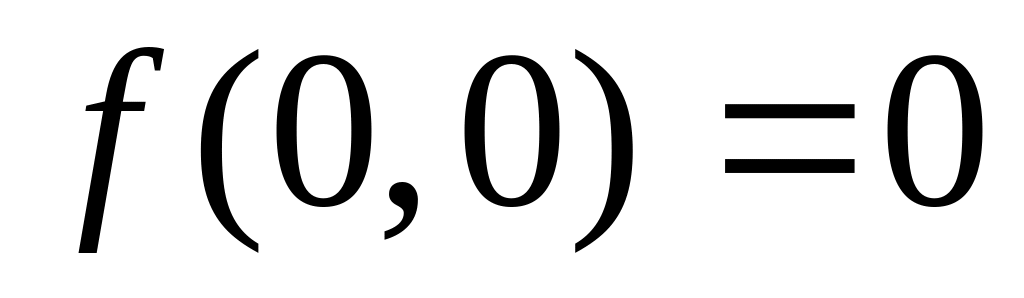 - без ресурсов нет
выпуска.
- без ресурсов нет
выпуска.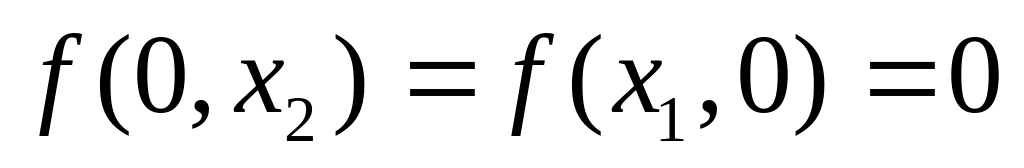 - при отсутствии
хотя бы одного из ресурсов нет выпуска
- при отсутствии
хотя бы одного из ресурсов нет выпуска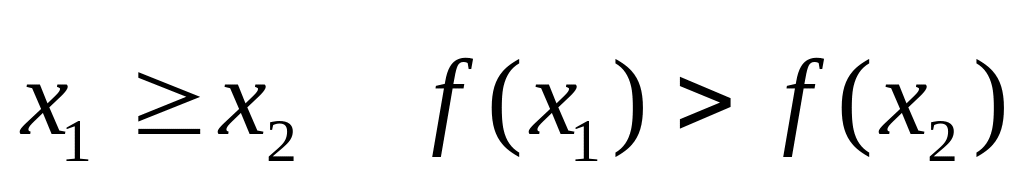 - с ростом затрат
хотя бы одного ресурса, объем выпуска
растет
- с ростом затрат
хотя бы одного ресурса, объем выпуска
растет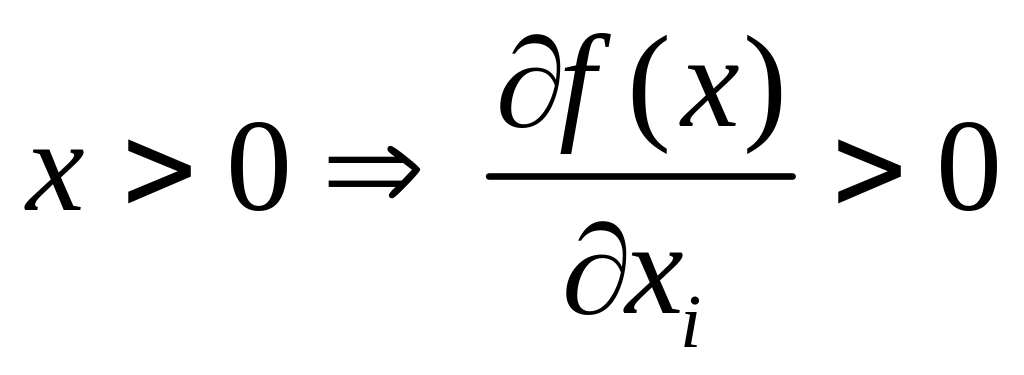 (первая частная
производная положительная) – с ростом
затрат одного ресурса, при неизменном
количестве другого ресурса, объем
выпуска растет.
(первая частная
производная положительная) – с ростом
затрат одного ресурса, при неизменном
количестве другого ресурса, объем
выпуска растет.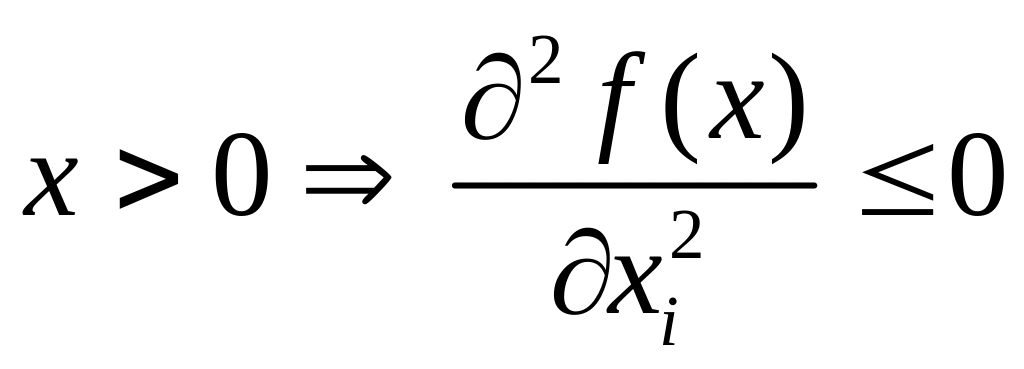 (вторая частная
производная неположительная) – с ростом
затрат одного
(вторая частная
производная неположительная) – с ростом
затрат одного
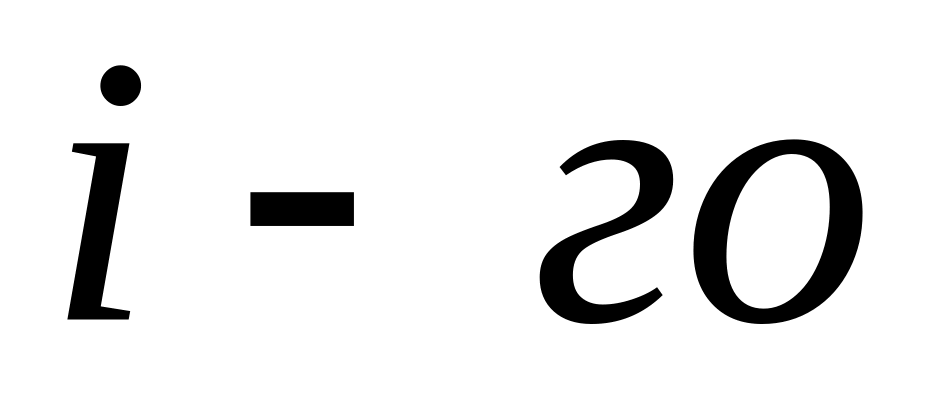 ресурса, при неизменном количестве
другого ресурса, величина прироста
выпуска на каждую дополнительную
единицу
ресурса не растет (закон убывающей
эффективности)
ресурса, при неизменном количестве
другого ресурса, величина прироста
выпуска на каждую дополнительную
единицу
ресурса не растет (закон убывающей
эффективности)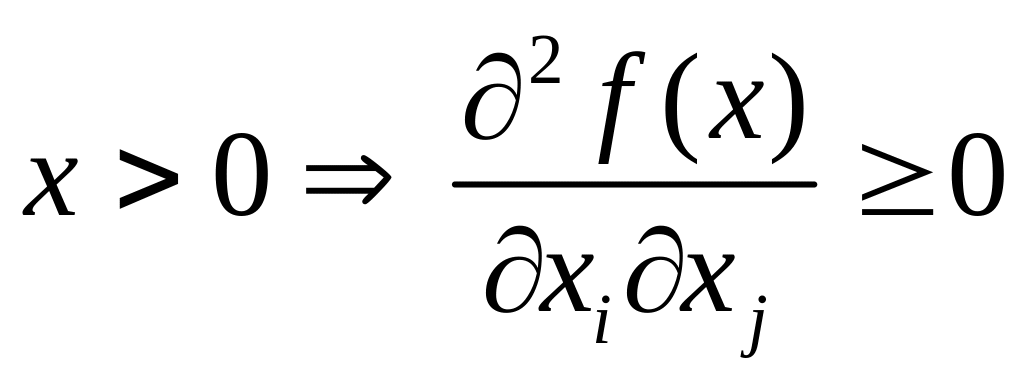 - при росте одного
ресурса предельная эффективность
другого ресурса возрастает
- при росте одного
ресурса предельная эффективность
другого ресурса возрастает
