Тема: Нелинейные модели регрессии и линеаризация.

До сих пор мы рассматривали лишь линейные модели регрессионной зависимости от . В тоже время многие важные связи в экономике являются нелинейными. Примерами такого рода регрессионных моделей являются:

• Производственные функции (зависимость между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т.д.);

• Функции спроса (зависимость между спросом на какой-либо вид товара или услуг, с одной стороны, и доходом или ценами на этот товар – с другой).

Как было отмечено ранее, этап параметризации регрессионной модели, т.е. выбора параметрического класса функций является одновременно наиболее важным и наименее формализованным и теоретически обоснованным этапом регрессионного анализа. Если же в результате реализации этого этапа исследователь пришел к выводу, что функция нелинейная, то далее он может действовать следующим образом:

1. Вначале он пытается подобрать такие преобразования к анализируемым переменным 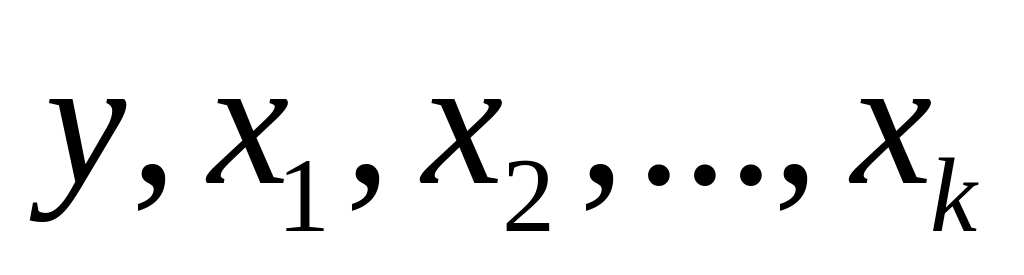, которые позволили бы представить искомую зависимость в виде линейного соотношения между преобразованными переменными; другими словами, если 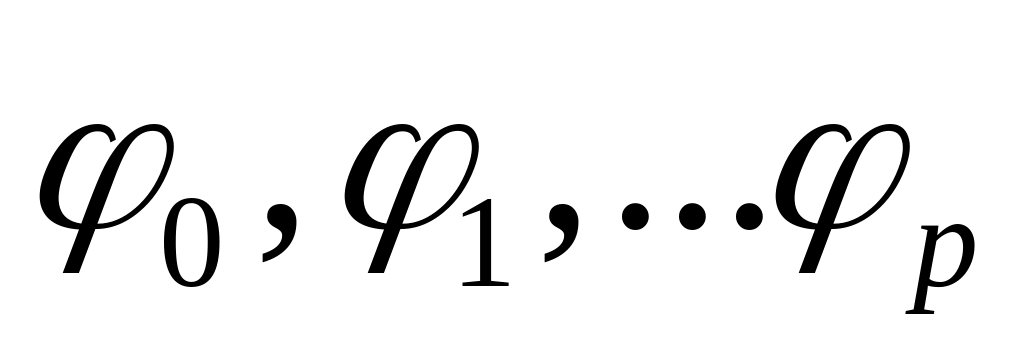- те самые искомые функции, которые определяют переход к преобразованным переменным, т.е. 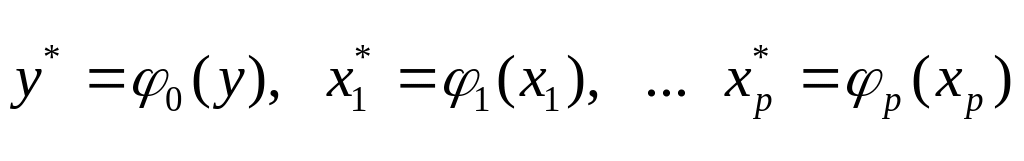, то связь между и 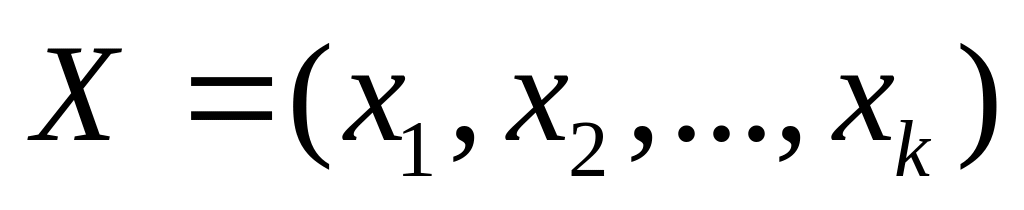может быть представлена в виде линейной функции регрессии 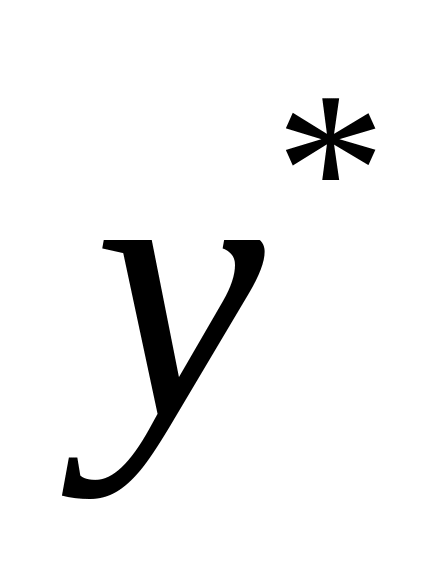от 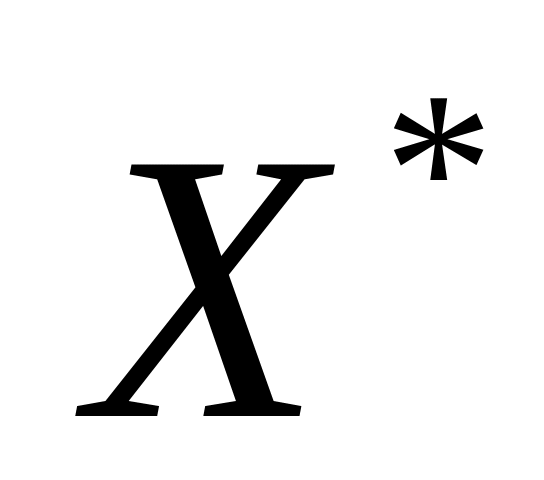, а именно:

Эту часть исследования обычно называют процедурой линеаризации модели

2. в случае невозможности линеаризации модели приходится исследовать искомую регрессионную зависимость в терминах исходных переменных, а именно: .

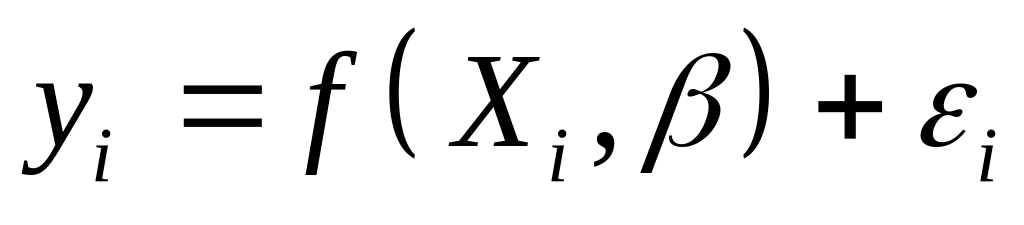Если спецификация регрессионных остатков соответствует условиям классической модели, то для вычисления МНК-оценок решается оптимизационная задача вида: .

Некоторые виды нелинейных зависимостей, поддающиеся непосредственной линеаризации

1. Зависимость гиперболического типа

1.1

Соответствующая кривая регрессии характеризуется двумя асимптотами (т.е. прямыми, к которым график функции неограниченно приближается, не достигая их) – горизонтальной и вертикальной

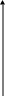
0

Рис.1

С помощью преобразования объясняющей переменной эта зависимость приводится к линейному виду . Соотвественно при вичислении МНК-оценок матрица будет иметь вид:

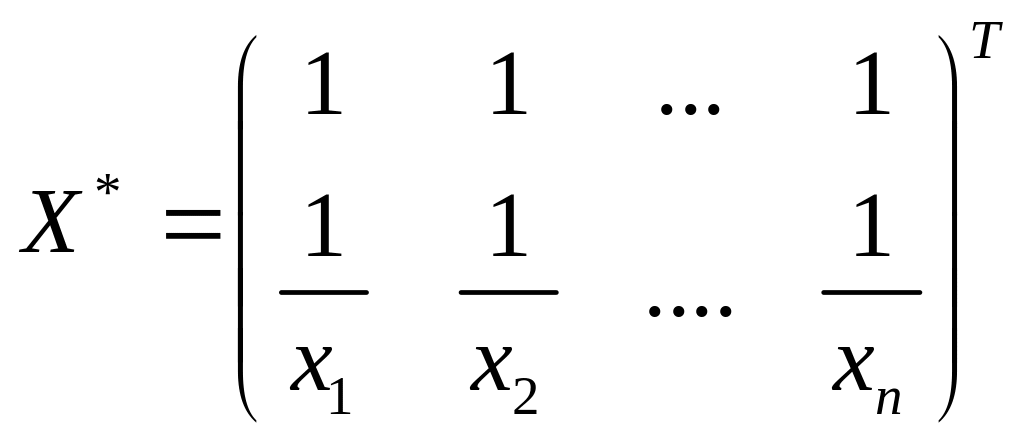
1.2

0

0

Рис. 2 Рис. 2

С помощью преобразования результативной переменной эта зависимость приводится к линейному виду . Соотвественно при вичислении МНК-оценок .

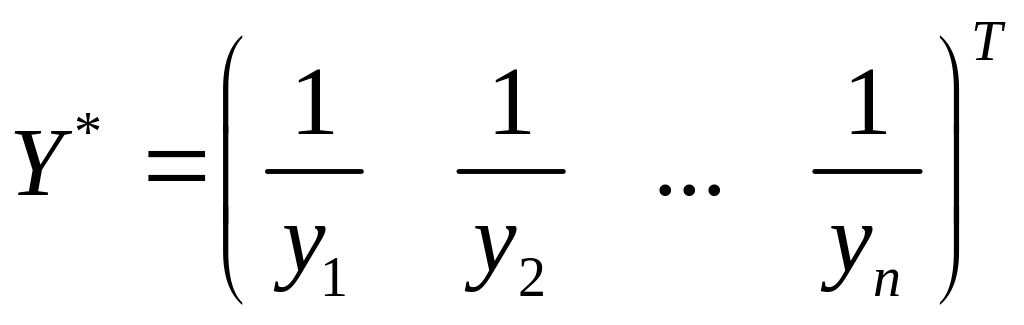1.3

0

0

Рис. 3 Рис. 3

Очевидно, что матрицы , используемые в формулах МНК, должны формироваться не из наблюденных значений, соответственно , а из обратных к ним величин , .

Замечание:

• функции, изображенные на Рис.1 (случай ) и Рис.3б используются в определенных ситуациях при построении так называемых кривых Энгеля, которые описывают зависимость спроса на определенный вид товаров или услуг от уровня доходов потребителей.

• функции, изображенные на Рис. 1 (случай ) и Рис.2а и 3а могут оказаться полезными при изучении спроса на товар в зависимости от его цены.