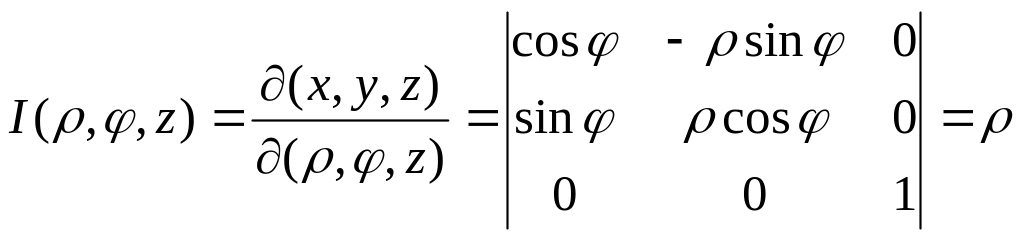12. Двойные интегралы. Определение, свойства, геометрический смысл.

z=f(x,y) – непрерывна в области D. Делим область Д на ΔS_i. Если существует предел интегральной суммы при λ0, то он назыв. двойным интегралом:

Свойства: 1)

2)

3)

4) Если f1≥f2 в S, то

5)

6) Теорема о среднем: если f(x,y) непрерывна в области S, то существует по меньшей мере одна точка (ξ, η)S такая, что

7) Если m является нижней, а М – верхней границей для f(x,y) на S, и если ΔS – площадь области S, то

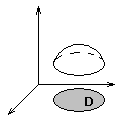
Геометрический смысл: если f(x,y)≥0, то двойной интеграл представляет собой объем прямого цилиндроида, построенного на области S как на основании и ограниченного сверху поверхностью z=f(x,y).

13. Условия существования и вычисления двойного интеграла.

Вычисление: если x[a,b]; y[φ1(x), φ2(x)] или y[c,d]; x[ψ1(x), ψ2(x)], то

14. Приложения двойных интегралов. Геометрические приложения:

1)

2) из геом. смысла двойного интеграла =>

3) Площадь пов-ти

где z=f(x,y) – ур-е пов-ти; f(x,y) имеет непрерывные частные производные f’_x(x,y) и f’_y(x,y) в замкнутой области σ, которая является проекцией пов-ти, заданной ур-ем z=f(x,y) на плоскость XOY. Физические приложения:

1) Статические моменты относительно коорд. осей

2) координаты щентра тяжести т.С(x_c,y_c)

x_c = I_x/S ; y_c = I_y/S ; 3) Моменты инерции относит. коорд. осей

3 1.Замена переменной под знаком двойного интеграла. Пусть z=f(x,y) – непрерыв. в замкнутой области σ плоскости ХОУ, огранич. кусочно-гладким контуром, а ф-ции x=φ(U,V), y=ψ(U,V) имеют непрерывные частные производные в области W пл-ти UOV и взаимно однозначно отображают область W пл-ти UOV на обл-ть σ пл-ти ХОУ, тогда

якобиан отображения, |I(U,V)| характеризует коэффициент изменения площади при переходе к другим координатам. Переход в двойном интеграле к полярным координатам: x=r*cos φ; y=r*sin φ;

15. Тройные интегралы. Определения, свойства, механический смысл. Пусть в замкнутой области V пространства XYZ определена некоторая ф-ция f(x,y,z). Разобьем V на n частей ΔV₁, ΔV₂, …, ΔV_n, не содержащих общих внутренних точек. Рассмотрим ΔV_i. Выберем на ней т. Р_i(ξ_i, η_i, ζ_i). Рассмотрим значение ф-ции f(Р_i)=f(ξ_i, η_i, ζ_i); просуммируем все произведения f(ξ_i, η_i, ζ_i)* ΔV_i. - интегральная сумма для f(x,y,z) по области V. Рассмотрим . Если этот предел существует, то он называется тройным интегралом от ф-ции f(x,y,z) по области V

С точки зрения механики (масса тела, μ(x,y,z) – плотность распределения массы).

Св-ва: 1)

2)

3) Если V=V1+V2 =>

4) Если f(x,y,z) ≥ 0 в V =>

5) Если f 1≥ f2 в V =>

6)

7)Теорема о среднем. Если f(x,y,z) непрерывна в замкнутой области V, то в V существует точка Р(ξ,η,ζ):

16. Условия существования и вычисление тройного интеграла. Приложения тройных интегралов. Теорема. Если f(x,y,z) непрерывна в замкнутой области Vпр-ва XYZ, то

существует.

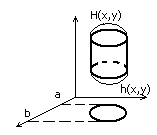
Теорема. Если область V пр-ва XYZ ограничена сверху и снизу пов-ми z=H(x,y) и h(x,y), где h(x,y) ≤ H(x,y), и H(x,y) и h(x,y) – непрерывны в замкнутой области σ = Пр_xoyV (проекция), а с боку огранич. цилиндрической поверхностью с образующими || оси oz и направляющей границей области σ, то для непрерыв. ф-ции f(x,y,z) справедлива следующая формула:

( первый интеграл – от точки до точки, второй – от линии до линии, третий – от поверхности до поверхности).

17. Замена переменной под знаком тройного интеграла. Пусть f(x,y,z) непрерывна в замкнутой области V пр-ва XYZ, а ф-ции x=φ(U,V,W), y=ψ(U,V,W), z=χ(U,V,W) (1) имеют непрерывные частные производные в области Т пространства UVW, и отображают взаимнооднозначно область V пр-ва XYZ на обл. Т => формула перехода от декартовых координат к другим, где - якобиан отображения (1), где I(U,V,W) равен коэфф. Изменения бесконечно малого объема при замене переменных. Переход к цилиндрическим координатам: М(ρ,φ,z), ρ=OM’ – полярный радиус,

φ- ОХ,^ρ, z = M’M. 0≤ρ<∞, 0≤φ≤2π, -∞<z<+∞;