Федеральное агентство по рыболовству

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Мурманский государственный технический университет»

(ФГОУВТПО «МГТУ»)

Кафедра высшей математики и программного обеспечения ЭВМ

ИДО

Обыкновенные дифференциальные уравнения

Электронный конспект лекций

по дисциплине «Математический анализ» для студентов специальности 230105 «ПО ВТ и АС»

Составитель ЭКЛ: Кацуба В.С. – к.ф.-м.н., доцент,

Мурманск, 2008

Оглавление

§1.	Определение обыкновенного дифференциального уравнения, его порядка и решений. Дифференциальные уравнения первого порядка: общие определения и их геометрическая трактовка, теорема существования и единственности решения задачи Коши.....................................................................................................................	3
§2.	Основные методы решения дифференциальных уравнений первого порядка (решение ДУ с разделяющимися переменными, однородные ДУ, линейные ДУ, ДУ Бернулли)..........................................................................................................................	10
§3.	Дифференциальные уравнения высших порядков, допускающие понижение порядка..................................................................................................................................	18
§4.	Линейные дифференциальные уравнения высших порядков. Основные свойства решений линейных однородных дифференциальных уравнений, теорема об общем решении....................................................................................................................	23
§5.	Нахождение фундаментальной системы частных решений для линейных однородных дифференциальных уравнений с постоянными коэффициентами................	28
§6.	Теорема об общем решении линейного неоднородного дифференциального уравнения. Принцип суперпозиции частных решений........................................................	30
§7.	Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами...........................................................................................................................	33
§8.	Метод вариации произвольных постоянных.................................................................	40
§9.	Понятие о системах обыкновенных дифференциальных уравнений. Решение систем методом повышения порядка дифференциальных уравнений.............................	43
§10.	Понятие об устойчивости решений дифференциальных уравнений и их систем.....	50

§10 Не отредактирован.

§1. 1.1

Определение обыкновенного дифференциального уравнения, его порядка и решений. Дифференциальные уравнения первого порядка: общие определения и их геометрическая трактовка, теорема существования и единственности решения задачи Коши Физическая задача, приводящая к понятию дифференциального уравнения

С некоторой высоты брошено тело массой m. Составить уравнение для скорости падения этого тела в любой момент времени от начала падения, если на него, кроме силы тяжести, действует сила сопротивления воздуха, прямо пропорциональная скорости падения.

Решение.

В момент времени составляем уравнение падения тела, используя II закон Ньютона:

, где - масса тела, - ускорение тела, - скорость тела,

- равнодействующая всех сил, приложенных к телу в его центре масс.

Так как все векторы, обозначенные в задаче, являются коллинеарными, то уравнение падения тела можно записать в скалярной форме:

(*)

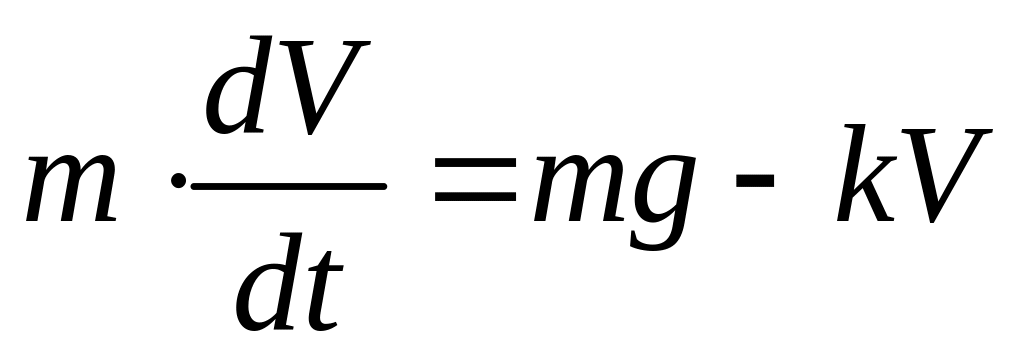
– это есть уравнение относительно искомой скорости V(t), так как оно выполняется в любой момент времени t.

Такое уравнение называется дифференциальным, так как в него входит производная искомой функции V(t). Решить это дифференциальное уравнение (далее ДУ) – это значит найти функцию V(t), удовлетворяющую ДУ при любом t. Для однозначного определения этой функции нужны еще так называемые начальные условия – это начальная скорость, с которой тело брошено с фиксированной высоты:

, где – момент времени, когда тело брошено,

– число, равное модулю начальной скорости падения.

Если же начальные условия не ставить, то дифференциальному уравнению (*) будет удовлетворять бесконечно много функций

1.2	Общие понятия, связанные с дифференциальными уравнениями
Определение обыкновенного ДУ и его порядка
Обыкновенным дифференциальным уравнением называется равенство, выражающее связь между некоторой независимой переменной , неизвестной функцией и ее производными по . Самый общий вид ДУ: (1) Порядком дифференциального уравнения называется порядок старшей производной от неизвестной функции, входящей в дифференциальное уравнение.

Примеры

1) - ДУ II порядка относительно функции ;

2) - ДУ III порядка относительно функции ;

3) - ДУ III порядка относительно функции ;

4) – ДУ I порядка относительно функции .

Замечания

1. Чтобы уравнение было дифференциальным, в него могут явно не входить , , но обязательно входит хотя бы одна производная функции

2. Обыкновенные дифференциальные уравнения содержат неизвестную функцию, зависящую от одной переменной. Такие и будем рассматривать. Если неизвестная функция зависит от нескольких переменных, то ДУ называют дифференциальным уравнением в частных производных.

Определение решений ДУ

Решением дифференциального уравнения называется любая функция, которая, будучи подставленной в ДУ, обращает его в тождество относительно аргумента. Различают три вида решений ДУ: общее, частное и особое. Общим решением ДУ n-ного порядка называется функция , зависящая от аргумента и произвольных постоянных и удовлетворяющая ДУ при любых значениях этих постоянных. Частным решением ДУ называется его решение, получающееся из общего решения этого ДУ при фиксированных значениях постоянных : . Особым решением ДУ называется такое его решение, которое не может быть получено из его общего решения ни при каких фиксированных значениях произвольных постоянных .

Пример 1

Рассмотрим - ДУ I порядка относительно функции .

Его общим решением является функция ,

так как при подстановке этой функции в ДУ получаем тождественно по и по :

- верно при любых и любых значениях .

Частными решениями рассматриваемого ДУ являются функции:

Особым решением является функция , так как она удовлетворяет ДУ, но не получается из общего решения ни при каком значении .

Начальные условия

Для выделения частного решения из общего решения ставят так называемые начальные условия к дифференциальному уравнению. Для ДУ n-ого порядка эти условия имеют следующий вид:

,

(2)

где - это фиксированные числа.

Таким образом:

• количество начальных условий совпадает с порядком ДУ, следовательно, совпадает с количеством произвольных постоянных в общем решении ДУ;

• суть начальных условий для ДУ n-ого порядка состоит в том, что они задают при фиксированном значении независимой переменной 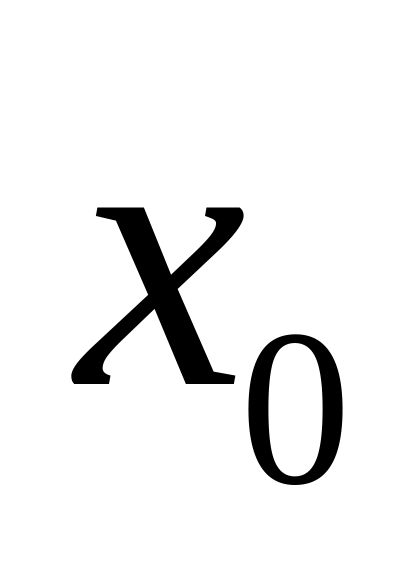значения неизвестной функции 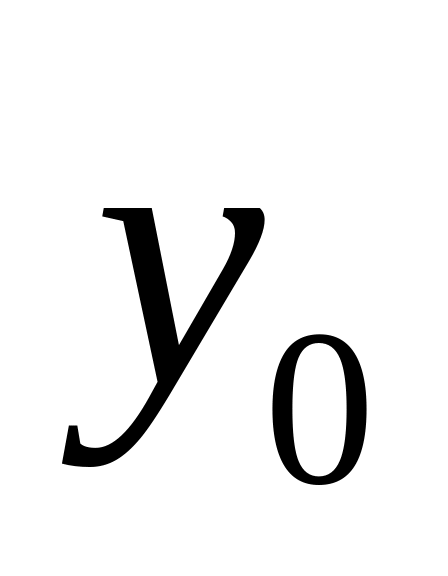и всех её производных до (n-1) -ого порядка включительно.

Подставляя начальные условия (2) в общее решение ДУ (1), определяют значения произвольных постоянных и тем самым переходят от общего решения ДУ к его частному решению. Задачу нахождения частного решения ДУ, удовлетворяющего поставленным начальным условиям, называют задачей Коши для обыкновенного дифференциального уравнения.

Пример 2

Для ДУ предыдущего примера найти частное решение, удовлетворяющее начальному условию .

Решение

Общее решение данного уравнения известно: .

Подставляя сюда значения и из начальных условий, получим равенство для определения значения :

.

Возвращая теперь значение в общее решение, получим частное решение, удовлетворяющее данному начальному условию:

- это и есть решение поставленной задачи Коши.

Ответ: .