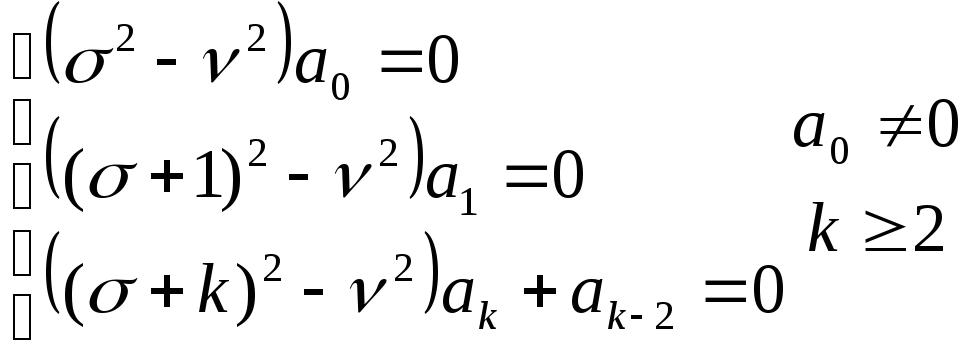- •Оглавление
- •Первая и вторая формулы Грина с оператором, следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением, понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с операторомс особенностью, свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, ,,,понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: ,её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задачас двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора.
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Уравнение Бесселя.
Рассмотрим
уравнение вида:
![]() - уравнение Бесселя. Это уравнение для
цилиндрических функций – его решения
– цилиндрические функции. Рассмотрим
лапласиан в цилиндрических координатах,
- уравнение Бесселя. Это уравнение для
цилиндрических функций – его решения
– цилиндрические функции. Рассмотрим
лапласиан в цилиндрических координатах,![]() и
и 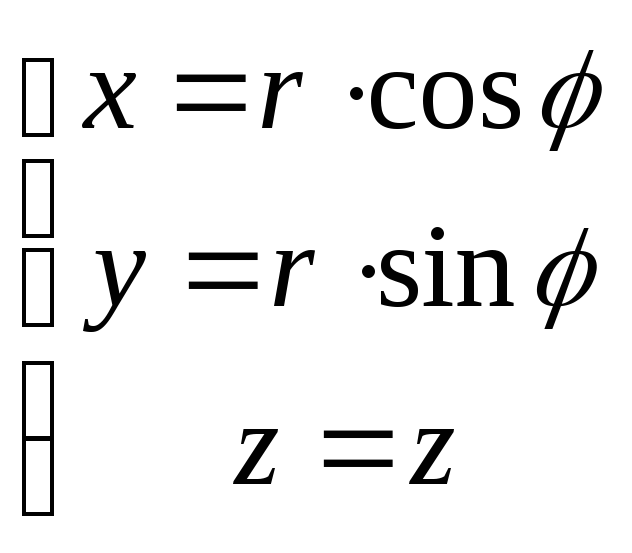 :
:
![]() - возникает в связи с решением уравнения
Лапласа в цилиндрических координатах.
- возникает в связи с решением уравнения
Лапласа в цилиндрических координатах.
Решением
этого уравнения (1-ым базисным решнием)
является функция Бесселя первого рада:
![]() .
.
Рассмотрим некоторые её свойства.
Рекуррентные соотношения.

Функции Бесселя с полуцелыми номерами
 .
Вычислим
.
Вычислим
 .
.
Для
этого выполним преобразования:
![]()
 ,
подставим
,
подставим
![]() ,
но
,
но![]() ,
тогда
,
тогда![]() .
.
Таким
образом, мы получили следующие значения:
 ,
используя рекуррентные соотношения
можно получить остальные значения
полуцелых индексов.
,
используя рекуррентные соотношения
можно получить остальные значения
полуцелых индексов.
Нули функции Бесселя.
|
|
1.
Они есть и их бесконечно много, следует
из асимптотики:
2.
Все нули, кроме
3. Все нули действительные, положительные. 4.
5.
При возрастании
|
Особенность, построение ограниченного решения .
Будем
искать решение уравнения Бесселя в виде
ряда Тейлора, умноженного на
![]() :
:![]() .
Подставим это решение в уравнение
.
Подставим это решение в уравнение![]() ,
,![]() ,
найдём коэффициенты и выберем ограниченное
решение.
,
найдём коэффициенты и выберем ограниченное
решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
|
При
При
При
При
|
|
Пусть
![]() .
Таким образом :
.
Таким образом : .
Вычислим коэффициент
.
Вычислим коэффициент![]() ,
и выразим его через
,
и выразим его через![]() .
.
![]() ,
коэффициент
,
коэффициент
![]() выбираем произвольно:
выбираем произвольно:![]() ,
где
,
где .
.
Таким
образом, получили коэффициенты ряда:
![]() ,
т.к.
,
т.к.![]() .
.
Запишем
формальный ряд:
![]() ,
если
,
если![]() ,
тогда решение ограничено. Оно решение,
т.к. ряд сходится для любых
,
тогда решение ограничено. Оно решение,
т.к. ряд сходится для любых![]() по признаку Даламбера:
по признаку Даламбера:![]() ,
сходится при всех
,
сходится при всех![]() ,
радиус сходимости равен бесконечности.
Таким образом, мы получили единственное,
с точность до множителя решение:
,
радиус сходимости равен бесконечности.
Таким образом, мы получили единственное,
с точность до множителя решение:![]() - функция Бесселя первого рода – это
первое базисное решение.
- функция Бесселя первого рода – это
первое базисное решение.
Случай
![]() рассмотрен в следующем пункте.
рассмотрен в следующем пункте.
Общее решение, ,,,понятие о функциях .
Будем
искать решение уравнения Бесселя в виде
ряда Тейлора, умноженного на
![]() :
:![]() .
Подставим это решение в уравнение
.
Подставим это решение в уравнение![]() ,
,![]() ,
найдём коэффициенты и выберем ограниченное
решение.
,
найдём коэффициенты и выберем ограниченное
решение.
Подставив решение в уравнение, сравниваем коэффициенты при разных степенях:
|
При
При
При
При
|
|
Пусть
![]() :
тогда уравнение решение Бесселя будет:
:
тогда уравнение решение Бесселя будет:![]() ,
где
,
где![]() - любое нецелое число. Это неограниченное
решение значит, оно может выступать в
роли второго базисного, но только в
случае не целого значения
- любое нецелое число. Это неограниченное
решение значит, оно может выступать в
роли второго базисного, но только в
случае не целого значения![]() .
.
Пусть
![]() - целое число, тогда
- целое число, тогда![]() при
при![]() .
.![]() сменим индекс:
сменим индекс:![]()
![]() ,
получили соотношение:
,
получили соотношение:![]() ,
то есть решения стали линейно зависимыми..
,
то есть решения стали линейно зависимыми..
В
качестве второго линейно независимого
решения уравнения Бесселя можно взять
функцию, построенную следующим образом:
![]() - это функция Неймана.
- это функция Неймана.
Её
асимптотика
 .
Оно тоже может играть роль базисного
уравнения.
.
Оно тоже может играть роль базисного
уравнения.
Могут быть и другие линейно-независимые комбинации (базисные решения):
 -
функции Ханкеля, их асимптотика
-
функции Ханкеля, их асимптотика
 .
.
Т.о. общее решение уравнения Бесселя имеет вид (линейная комбинация 2-х базисных решений):
![]()
Асимптотика решений уравнения Бесселя, нули функции Бесселя.
Функции
Бесселя (любые решения уравнения Бесселя)
имеют особенность в нуле. Решение
уравнения Бесселя при
![]() имеет
следующий вид:
имеет
следующий вид: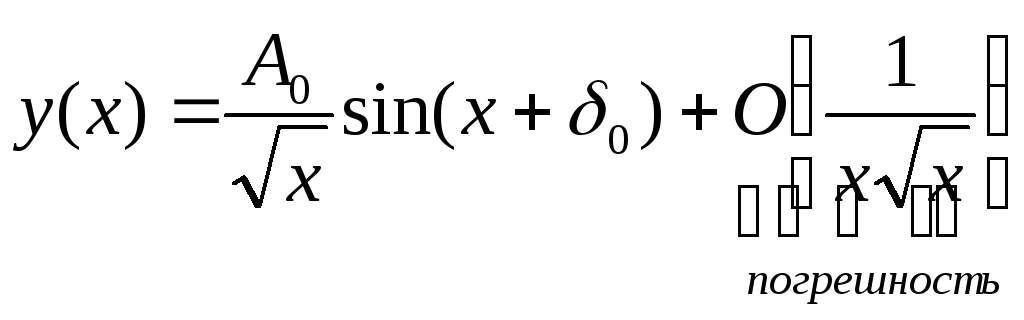 .
Докажем это.
.
Докажем это.
Для
этого сделаем замену:
![]() ,
подставим
,
подставим![]() ,
первые производные ушли, осталось:
,
первые производные ушли, осталось: .
Таким образом:
.
Таким образом:![]() ,
будем искать
,
будем искать![]() в виде:
в виде:![]() .
Надо найти две функции:
.
Надо найти две функции:![]() и
и![]() .
.
![]() положим
положим
![]() ,
получим
,
получим
![]() .
Тогда
.
Тогда![]() ,
подставим в уравнение:
,
подставим в уравнение:![]() ,
т.о. получили систему:
,
т.о. получили систему: .
Получили систему, разрешённую относительно
производных, но не нелинейную. Оценим.
Проинтегрируем и запишем для первого
и второго уравнений:
.
Получили систему, разрешённую относительно
производных, но не нелинейную. Оценим.
Проинтегрируем и запишем для первого
и второго уравнений:
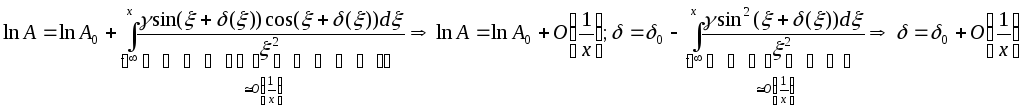 .
При больших значениях
.
При больших значениях![]() ,
,![]() и
и![]() имеют вид констант.
имеют вид констант.
Получим
вид
![]() :
: и
и![]() :
: .
.
Тогда
![]() - общая формула для любой цилиндрической
функции.
- общая формула для любой цилиндрической
функции.
Асимптотики функций Бесселя и Неймана: