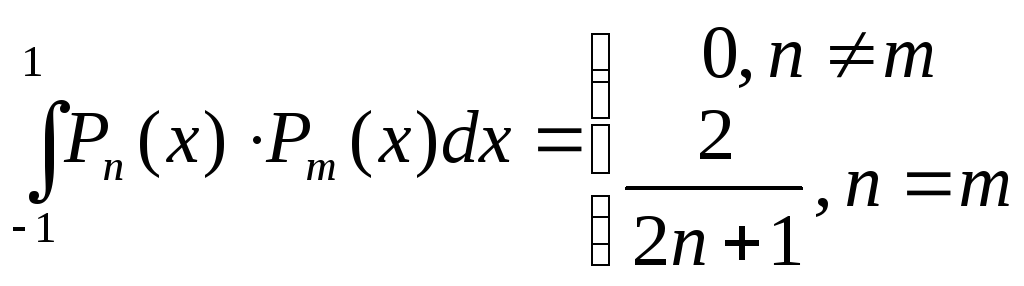- •Оглавление
- •Первая и вторая формулы Грина с оператором, следствия.
- •Гармонические функции. Интегральное представление. Их основные свойства.
- •Примеры
- •Свойства гармонических функций.
- •Теорема о среднем для гармонических функций
- •Теорема о максимумах и минимумах для гармонических функций. Единственность и корректность задач Дирихле.
- •Следствия:
- •Функция Грина для краевой задачи с уравнением Пуассона. Её построение методом отображений.
- •Функция Грина для задачи с уравнением, понятия, определения.
- •Решение задач с её помощью
- •Построение функции Грина в одномерном случае на отрезке
- •Теория потенциалов, определение, основные свойства.
- •Объёмный потенциал
- •Потенциал простого слоя
- •Потенциал двойного слоя
- •Решение задач Дирихле с уравнением Пуассона методом теории потенциалов
- •Сводная таблица6 общие сведения о потенциалах:
- •Понятие о корректно и некорректно поставленных задачах математической физики, примеры.
- •Уравнение с операторомс особенностью, свойства, ограниченность, постановка задачи.
- •Уравнение Бесселя.
- •Особенность, построение ограниченного решения .
- •Общее решение, ,,,понятие о функциях .
- •Асимптотика решений уравнения Бесселя, нули функции Бесселя.
- •Краевая задача на собственные значения: ,её решение, ортогональность собственных функций, теорема Фурье-Бесселя б/д.
- •Модифицированное уравнение Бесселя, ограниченность решения , свойства, общее решение, понятие о функции .
- •Сводная таблица.
- •Краевая задачас двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора.
- •Уравнение гипергеометрического типа.
- •Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).
- •Решение в виде полиномов. Формула Родрига.
- •Ортогональные решения полиномов. Свойства нулей.
- •Примеры: уравнения, краевые задачи, определение и свойства полиномов
- •Полиномы Лежандра.
- •Полиномы Чебышева-Лягера.
- •Чебышева-Эрмита.
- •Сводная таблица для уравнений гипергеометрического вида.
- •Уравнения, краевая задача для присоединенных полином Лежандра. Решения. Основные свойства.
- •Уравнение Лапласа в сферических координатах. Схема решения методом разделения переменных.
- •Сферические функции, определения, построение системы базисных функций. Ортогональность, полнота, теорема о разложении, б/д.
Примеры: уравнения, краевые задачи, определение и свойства полиномов
Полиномы Лежандра.
1)
Определим многочлены Лежандра так:
разложим в ряд по степеням
![]() функцию:
функцию:
![]() .
.
Коэффициенты
этого разложения
![]() являются многочленами, называемыми
полиномами Лежандра.
являются многочленами, называемыми
полиномами Лежандра.![]() - называется производящей функцией
полиномов Лежандра.
- называется производящей функцией
полиномов Лежандра.
2)
Краевая задача: найти такие значения
![]() ,
для которых на отрезке
,
для которых на отрезке![]() существуют не тривиальные решения
уравнения Лежандра
существуют не тривиальные решения
уравнения Лежандра![]() ,
ограниченные при
,
ограниченные при![]() .
.
Функция
![]() - есть собственная функция задачи,
соответствующая собственному значению
- есть собственная функция задачи,
соответствующая собственному значению![]() .
.
Упрощённое
уравнение Лежандра:
![]()
3)
Рекуррентные соотношения:
![]()
![]()
4)
Ортогональность и норма полиномов
Лежандра:
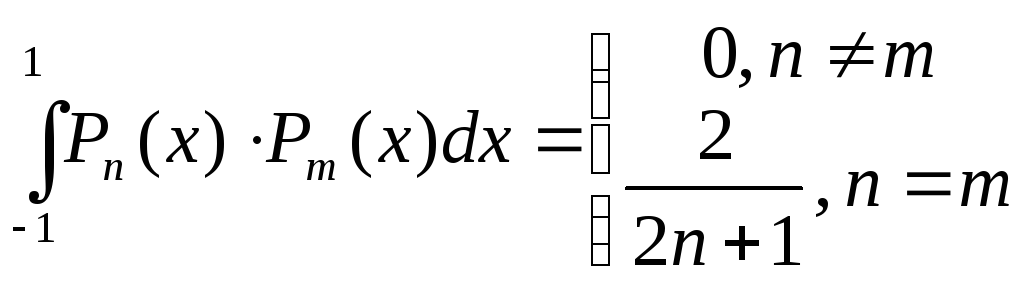 ,
полиномы Лежандра разных порядков
ортогональны между собой; второе линейно
независимое решение уравнения Лежандра
при
,
полиномы Лежандра разных порядков
ортогональны между собой; второе линейно
независимое решение уравнения Лежандра
при
![]() обращается в бесконечность при
обращается в бесконечность при![]() как
как![]() .
.
5)
Все нули полиномов Лежандра простые и
расположены на интервале
![]() .
.
6)
Ограниченность: полиномы Лежандра
![]() равномерно ограниченны для всех значений
аргумента
равномерно ограниченны для всех значений
аргумента![]() .
.
Полиномы Чебышева-Лягера.
1)
Определим полиномы Чебышева-Лягера
так: разложим в ряд по степеням
![]() функцию:
функцию:
![]() .
.
Коэффициенты
этого разложения
![]() являются многочленами, называемыми
полиномами Чебышева-Лягера.
являются многочленами, называемыми
полиномами Чебышева-Лягера.![]() - называется производящей функцией
полиномов Чебышева-Лягера.
- называется производящей функцией
полиномов Чебышева-Лягера.
2)
Краевая задача: найти такие значения
![]() ,
для которых в области
,
для которых в области![]() существуют не тривиальные решения
уравнения Чебышева-Лягера
существуют не тривиальные решения
уравнения Чебышева-Лягера
![]() ,
ограниченные при
,
ограниченные при
![]() и возрастающие при
и возрастающие при![]() не быстрее чем конечная степень
не быстрее чем конечная степень![]()
Функция
![]() - есть собственная функция задачи,
соответствующая собственному значению
- есть собственная функция задачи,
соответствующая собственному значению![]() .
.
Упрощённое
уравнение Чебышева-Лягера:
![]()
3)
Рекуррентные соотношения:
![]()
4)
Ортогональность и норма полиномов
Чебышева-Лягера:
![]() :,
полиномы Чебышева-Лягера разных порядков
ортогональны между собой с весом
:,
полиномы Чебышева-Лягера разных порядков
ортогональны между собой с весом![]() .
.
Чебышева-Эрмита.
1)
Определим полиномы Чебышева-Эрмита
так: разложим в ряд по степеням
![]() функцию:
функцию:
![]() .
.
Коэффициенты
этого разложения
![]() являются многочленами, называемыми
полиномами Лежандра.
являются многочленами, называемыми
полиномами Лежандра.![]() - называется производящей функцией
полиномов Чебышева-Эрмита.
- называется производящей функцией
полиномов Чебышева-Эрмита.
2)
Краевая задача: найти такие значения
![]() ,
для которых на
,
для которых на![]() существуют не тривиальные решения
уравнения Чебышева-Эрмита
существуют не тривиальные решения
уравнения Чебышева-Эрмита
![]() ,
возрастающее при
,
возрастающее при
![]() не быстрее чем конечная степень
не быстрее чем конечная степень![]()
Функция
![]() - есть собственная функция задачи,
соответствующая собственному значению
- есть собственная функция задачи,
соответствующая собственному значению
![]() .
.
Упрощённое
уравнение Чебышева-Эрмита:
![]()
3)
Рекуррентные соотношения:
![]() ;
;![]()
4)
Ортогональность и норма полиномов
Чебышева-Эрмита:
![]() ,
полиномы Чебышева-Эрмита разных порядков
ортогональны на
,
полиномы Чебышева-Эрмита разных порядков
ортогональны на![]() с весом
с весом![]() между собой.
между собой.
Сводная таблица для уравнений гипергеометрического вида.
|
|
Лежандр |
Чебышев - Лягер |
Чебышев - Эрмит | |||
|
Вид уравнения
|
|
|
| |||
|
Упрощенное уравнение |
|
|
| |||
|
Собственные решения: |
|
|
| |||
|
Собственные функции |
|
|
| |||
|
Рекуррентные соотношения: |
|
|
| |||
|
Производящие функции:
|
|
|
| |||
|
Ортогональность и норма: |
|
|
| |||
|
Упрощенное уравнение гипергеометрического вида: |
| |||||
|
его самосопряжённый вид |
| |||||
|
Произвольное решение уравнения гипергеометрического вида тоже является решением другого уравнения гипергеометрического вида: |
Пусть:
| |||||
|
Собственные решения: |
| |||||
|
Собственные функции (Формула Родрига): |
| |||||
|
Ортогональность: |
| |||||
|
Присоединённые уравнение Лежандра:
|
Присоединённые функции:
|
Норма присоединённых функций:
| ||||