12. Краевая задачас двумя особыми точками на концах отрезка. Граничные условия. Условия самосопряжённости оператора.

Рассмотрим уравнение: (*)и пусть - имеет два ноля.

Известно ограниченное решение в точке b, а также ограниченное решение в точке a. Возможен случай, когда решение в точке перейдёт в ограниченное решение в точке:. Но в общем случае всё множество решения, как правило, неограниченно. Исключительная ситуация может быть в случае нулевого решения. Таким образом возникает задача нахождения таких собственных значений λ, при которых задача -при- имеет нетривиальное решение; роль граничных условий здесь играет требование на ограниченность решения

Полученные функции, отвечающие различным собственным значениям, будут ортогональны, то есть оператор должен быть самосопряжённым.

Самосопряженность оператора

Используя 2-ую формулу Грина получаем:

13. Уравнение гипергеометрического типа.

1. Приведение к самосопряжённому виду. Весовые функции . Уравнение для производных(в следующем пункте).

Рассмотрим уравнение: (1)-уравнение гипергеометрического вида, где - полиномы порядка, а- полиномы порядка.

Домножим (1) на , подобрав её так, чтобы уравнение (1) приняло самосопряжённый вид:. Для этого нужно, чтобы- дифференциальное уравнение для, тогда получим: (1*)- самосопряжённый вид уравнения (1). Определим:- весовые функции.

Это свойство одномерной задачи. Т.к. вид оператора отличается от. Самосопряжённая форма (*) большое ограничение.

19. Решение в виде полиномов. Формула Родрига.

Пусть - решение уравнения. Продифференцируем:. Обозначим, тогда.Производная решения гипергеометрического вида тоже является решением другого уравнения гипергеометрического вида. Далее можно повторить это действие, введя аналогичную замену: и т.д. Следовательно- решение различных уравнений гипергеометрического вида.

Определим коэффициенты и. Посмотрим, как они изменятся дальше.,.

Запишем: , дифференцируем:.. Найдем. Рассмотрим- сложим все эти разности и получим:

Таким образом: . Приведём (2) к самосопряжённому виду. (2) – уравнение для производных. (2*), где- весовые функции.

Каждому целому можно указать такие значения, что. Т.е., при таком выборе, уравнениеприобретает новые качества:и новый вид. Тогда, положим эту константу равной нулю, тогда- многочлен степени. Таким образом, мы нашли бесконечную цепочку полиномов – решений уравненияпри соответствующих значения. Это система- нормальная система полиномов образует базис. Вспомним, перепишем в виде:. Рассмотрим. Длявоспользуемсяприпока(т.е. пока можно делить).

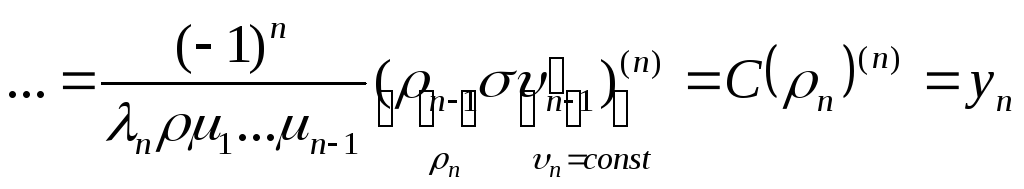Запишем в чистом виде: - формула Родрига.

20. Ортогональные решения полиномов. Свойства нулей.

Эти полиномы ортогональны с весом на отрезке:. Где точкииэто: 1) если- полином второго порядка, тои- это нули полинома, т.е.; либо 2) если- полином первого порядка, то:и; либо 3) если- полином нулевого порядка, т.е., тои. Решениялибо ограничены в особых точках, либо растут не быстрее полинома на бесконечности. Ортогональность следует из самосопряженности оператора, т.к. [].

Докажем. Запишем вторую формулу Грина: .

Теорема: Если - нормальная система полиномов на , то все нули принадлежат и они действительные и простые (значит, напроисходитсмен знаков (корни не кратные), ортогональность означает осцилляцию со сменой знака полное число раз).

Доказательство. Пусть теорема не верна.

Пусть имеетперемен знака:. Следовательно, если теорема не верна, то. Рассмотрим, т.к. система нормальная, тообразует базис. Тогда- полином степени- это нормальная система. Рассмотрим(нормировка)

	т.к. это интеграл от знакопостоянной функции.

Таким образом, получили противоречие, значит . Чтд.