4.Силовой анализ сложного плоского рычажного механизма

4.1 Определим значения и направления силовых факторов, действующих на звенья структуры.

Сила инерции определяется по формуле

где - масса - го звена,

- ускорение центра масс - го звена.

Масса - го звена находится по формуле,

где - коэффициент удельной массы - го звена,

- длина - го звена

Коэффициент удельной массы выбирается в зависимости от вида и служебного назначения звена из следующих интервалов: для шатунов– от 15 до 20 кг/м; для кривошипов- от 8 до 12 кг/м, для коромысел и кулис – 25-40кг/м

Масса ползуна находиться по формуле, кг,

где - масса шатуна

пользуясь формулами (28),(29) найдем массы звеньев:

Найдем силы инерции для шатунов 2, 4 и ползунов 3,5 согласно формуле (27) для 1 положения механизма, Н,

Вектора сил инерции , , , лежат на прямых, параллельных, соответственно, линиям действия векторов ускорений центров масс , , , , а направление действия этих векторов противоположно направлению действия векторов ускорений центров масс этих звеньев. Ускорения и совпадают с ускорениями, и соответственно.

Момент пары сил инерции вычисляется по формуле

где - момент инерции - го звена,

- угловое ускорение - го звена.

Знак «-» в формуле означает, что направление действия момента пары сил инерции - го звена противоположно направлению действия углового ускорения этого звена.

Момент инерции относительно центральных осей в сечении, , определяется следующим образом:

Для кривошипа

Для - го (простого) звена

Угловая скорость кривошипа 1 является постоянной величиной, следовательно, угловое ускорение этого звена равно нулю, т. е.ε , тогда согласно формуле (30) имеем, H⋅м,

0

Ползуны 5 и 3 совершают только поступательные движения, следовательно, угловое ускорение этих звеньев равны нулю, т. е. ε и

ε , тогда согласно формуле (30) найдем моменты пар сил инерции ползунов 5 и 3, H⋅м,

Момент пары сил инерции для первого положения механизма шатунов 2 и 4 найдем согласно формуле (32), H⋅м,

Направление действия момента пары сил инерции противоположно направлению действия углового ускорения. Следовательно, момент пары сил инерции шатуна 2 действует в направлении хода часовой стрелки, а шатуна 4 действует в направлении против хода часовой стрелки.

Сила тяжести - го звена

где - ускорение свободного падения, м/ .

Сила тяжести кривошипа 1 равна, Н,

Найдем силы тяжести остальных звеньев, Н,

Вектора сил тяжести прикладываются к центрам масс звеньев, и направлены вертикально вниз.

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 1 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 42).

Рисунок 42 - повернутый план скоростей для первого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 43).

Рисунок 43 – план скоростей и перенесенные силовые факторы с расчетной схемы для первого положения механизма

Моменты пар сил инерции шатунов 2 и 4 равны нулю, следовательно,

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Т.к.

, то = 0.

Найдем уравновешивающий момент пары сил по формуле (34), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 2 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 44).

Рисунок 44 - повернутый план скоростей для второго положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 45).

Рисунок 45 – план скоростей и перенесенные силовые факторы с расчетной схемы для второго положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции:

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 45).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(35)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов, м,

где - плечи моментов, измеренные на повернутом плане скоростей,

- масштабный коэффициент.

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (35) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 3 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 46).

Рисунок 46 - повернутый план скоростей для третьего положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 47).

Рисунок 47 - план скоростей и перенесенные силовые факторы с расчетной схемы для третьего положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 47).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(37)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (37) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 4 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 48).

Рисунок 48 - повернутый план скоростей для четвертого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 49).

Рисунок 49 - план скоростей и перенесенные силовые факторы с расчетной схемы для четвертого положения механизма

Моменты пар сил инерции шатунов 2 и 4 равны нулю, следовательно,

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Т.к.

, то = 0.

Найдем уравновешивающий момент пары сил по формуле (34), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 5 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 50).

Рисунок 50 - повернутый план скоростей для пятого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 51).

Рисунок 51 - план скоростей и перенесенные силовые факторы с расчетной схемы для пятого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 51).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(38)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (37) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 6 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 52).

Рисунок 52 - повернутый план скоростей для шестого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 53).

Рисунок 53 - план скоростей и перенесенные силовые факторы с расчетной схемы для шестого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 53).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(38)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (38) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 7 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 54).

Рисунок 54 - повернутый план скоростей для седьмого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 55).

Рисунок 55 - план скоростей и перенесенные силовые факторы с расчетной схемы для седьмого положения механизма

Моменты пар сил инерции шатунов 2 и 4 равны нулю, следовательно,

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Т.к.

, то = 0.

Найдем уравновешивающий момент пары сил по формуле (34), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 8 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 56).

Рисунок 56 - повернутый план скоростей для восьмого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 57).

Рисунок 57 - план скоростей и перенесенные силовые факторы с расчетной схемы для восьмого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 57).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(39)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (39) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 9 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 58).

Рисунок 58 - повернутый план скоростей для девятого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 59).

Рисунок 59 - план скоростей и перенесенные силовые факторы с расчетной схемы для девятого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 59).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(40)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (40) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 10 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 60).

Рисунок 60 - повернутый план скоростей для десятого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 61).

Рисунок 61 - план скоростей и перенесенные силовые факторы с расчетной схемы для десятого положения механизма

Моменты пар сил инерции шатунов 2 и 4 равны нулю, следовательно,

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Т.к.

, то = 0.

Найдем уравновешивающий момент пары сил по формуле (34), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 11 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 62).

Рисунок 62 - повернутый план скоростей для одиннадцатого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 63).

Рисунок 63 - план скоростей и перенесенные силовые факторы с расчетной схемы для одиннадцатого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 63).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(41)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (41) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

Построим повернутый план скоростей, условно приняв вектора жесткими и повернув заданный план скоростей для положения 12 структуры механизма относительно полюса плана на 90 градусов по направлению движения структуры механизма (рисунок 64).

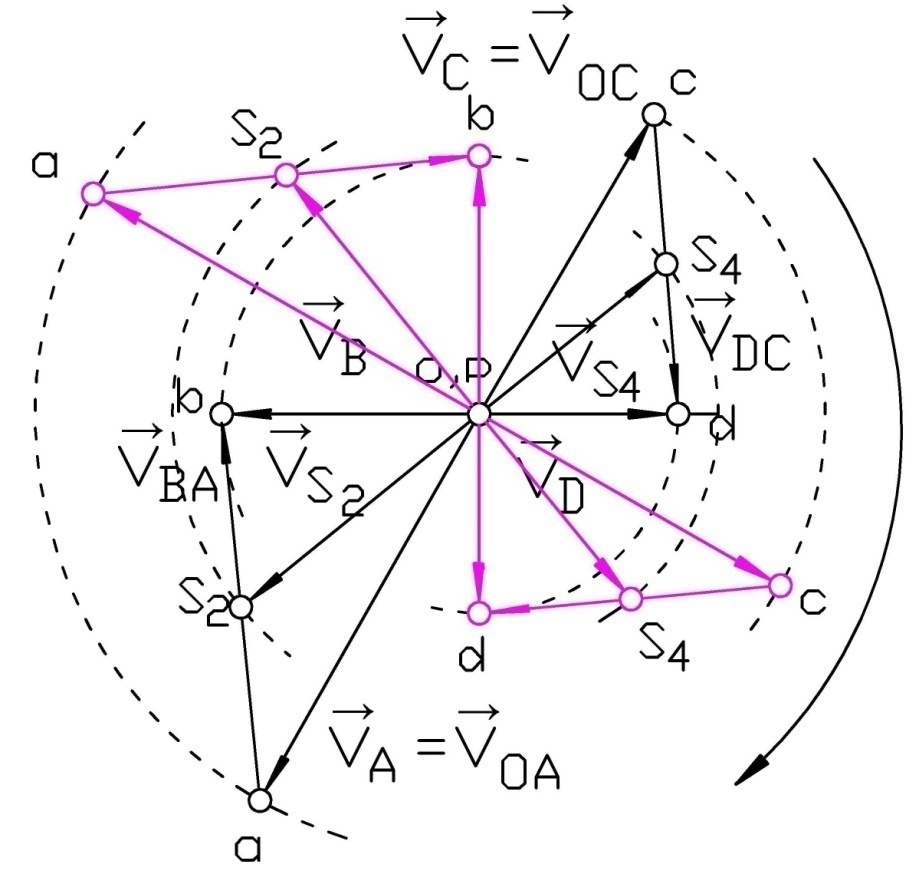
Рисунок 64 - повернутый план скоростей для двенадцатого положения механизма

Используя теорему В. Н. Жуковского, перенесем все силовые факторы с расчетной схемы в одноименные точки повернутого плана скоростей (рисунок 65).

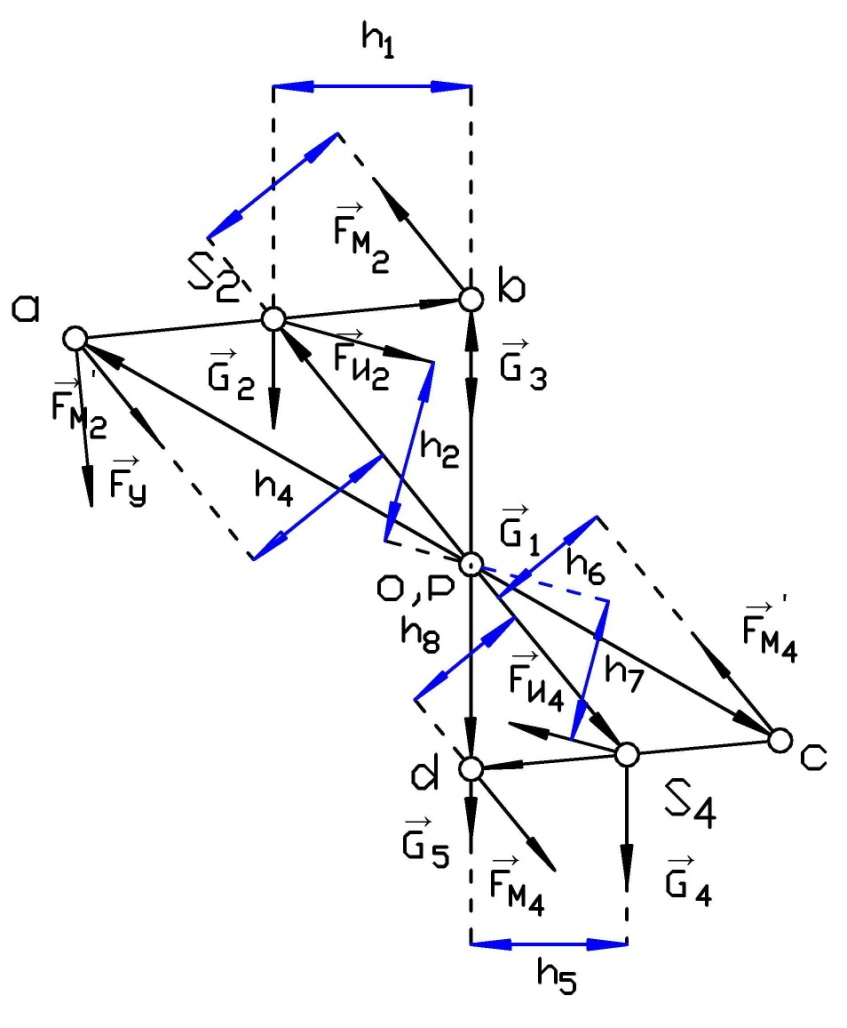
Рисунок 65 - план скоростей и перенесенные силовые факторы с расчетной схемы для двенадцатого положения механизма

Моменты пар сил инерции шатунов 2 и 4 заменим эквивалентными парами сил инерции по формуле (35).

Подставим значения коэффициентов в формулу (35), Н,

Приложим эти силы к векторам повернутого плана скоростей соответствующих звеньев (рисунок 65).

к ab , к cd.

Для определения величины уравновешивающей силы составим сумму моментов всех сил, действующих на данную систему относительно полюса повернутого плана скоростей:

(42)

Линия действия векторов , , проходят через полюс плана скоростей точку р, следовательно,

Найдем плечи моментов по формуле (36), м,

Подставим значение коэффициентов в формулу (36), м,

Выразим из формулы (42) уравновешивающую силу, Н,

Найдем уравновешивающий момент пары сил по формуле (37), ,

4.2 Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для заданного положения ведущего звена.

4.3 Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для положения 1 (рисунок 66, 67, 68, 69):

Рисунок 66

Рисунок 67 – 1 структурная группа с приложенными векторами сил и моментами пар сил для первого положения механизма

Рисунок 68 – 2 структурная группа с приложенными векторами сил и моментами пар сил для первого положения механизма

Рисунок 69 – первичный механизм с приложенными векторами сил и моментами пар сил для первого положения механизма

4.4 Так как структурные группы являются частью структуры механизма, то равновесия не существует. Для его установления используем принцип освобождаемости от связей. Заменим силы реакциями связей.

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна точка ее приложения точка А и линия действия.

4.5 Составим уравнения равновесии структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(43)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

две неизвестных: .

Статическая неопределимость определяется по формуле:

где - количество неизвестных,

- количество уравнений.

Подставим значение коэффициентов в формулу (44):

Следовательно, система 2 – 3 статически неопределима.

Линии действия векторов сил , проходят через полюс - точку В, следовательно,

4.6.Масштабный коэффициент плана сил:

(45)

где - наибольшая сила,

- произвольный отрезок.

Подставим значения коэффициентов в формулу (45) , Н/м,

Переведем силы в масштабный коэффициент:

(46)

Подставим значение коэффициентов в формулу (46), мм,

= = 66,7

= 0

= =33,4

= =190

По полученным значениям строим план сил. Для нахождения неизвестных достраиваем фигуру.

Рисунок 70 – план сил 1 структурной группы первого положения механизма

Вычислим значение реакций связей кинематических пар.

Значение полной реакции будет равно, Н,

Значение реакции будет равно, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна точка ее приложения точка C и линия действия.

4.10 Составим уравнения равновесии структурной группы 4-5.

Для структурной группы звеньев 4 – 5 Уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

две неизвестных: .

Статическая неопределимость определяется по формуле (44).

Подставим значение коэффициентов в формулу(44):

Следовательно, система 4 – 5 статически неопределима.

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

4.11В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Масштабный коэффициент плана сил:

Подставим значение коэффициентов в формулу (46), мм,

36,8

18,4

190

По полученным значениям строим план сил. Для нахождения неизвестных достраиваем фигуру.

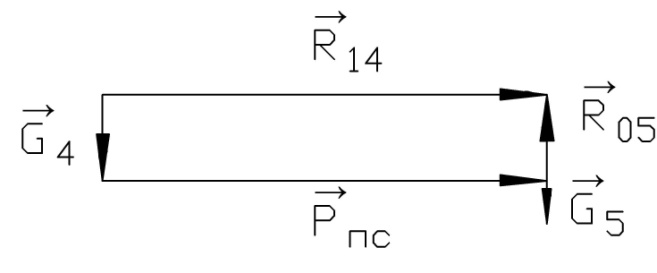
Рисунок 71 – план сил 2 структурной группы первого положения механизма

Вычислим значение реакций связей кинематических пар.

Значение полной реакции будет равно, Н,

будет равно, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных: ,

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна пяти.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(49)

(50)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36).

Выразим значение тангенциальной составляющей реакции и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , , Статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 72).

Рисунок 72 – план сил для первичного механизма первого положения

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=3.041·2 = 6.082

= 6.082·0.16 = 0.9731

Составим расчетную схему для второго положения механизма. При этом на звенья механизма действуют следующие силовые факторы.

Силы инерции для шатунов 2, 4 и ползунов 3,5 согласно формуле (27) для 2 положения механизма, Н,

Момент пары сил инерции для 2 положения механизма шатунов 2 и 4 найдем согласно формуле (32), H⋅м,

Силы тяжести звеньев, Н,

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для второго положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 2 положения (рисунки 73, 74, 75, 76):

Рисунок 73

Рисунок 74 – 1 структурная группа с приложенными векторами сил и моментами пар сил для второго положения механизма

Рисунок 75 - 2 структурная группа с приложенными векторами сил и моментами пар сил для второго положения механизма

Рисунок 76 – первичный механизм с приложенными векторами сил и моментами пар сил для второго положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Рисунок 77

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(51)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(52)

(53)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 77 и по формуле (36), м,

Выразим из уравнения (53) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 78 – план сил 1 структурной группы второго положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 78) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Рисунок 79

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(54)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(55)

(56)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 79 и по формуле (36), м,

Выразим из уравнения (56) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 80 - план сил 2 структурной группы второго положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 80) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(58)

(59)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 76 .

Выразим значение тангенциальной составляющей реакции из формулы (59) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , Статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 77).

Рисунок 77 - план сил первичного механизма во втором положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=18.413

Составим расчетную схему для третьего положения механизма. При этом на звенья механизма действуют следующие силовые факторы.

Силы инерции для шатунов 2, 4 и ползунов 3,5 согласно формуле (27) для 3 положения механизма, Н,

Момент пары сил инерции для 3 положения механизма шатунов 2 и 4 найдем согласно формуле (32), H⋅м,

Силы тяжести звеньев, Н,

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для третьего положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 2 положения (рисунки 78, 79, 80, 81):

Рисунок 78

Рисунок 79 – 1 структурная группа с приложенными векторами сил и моментами пар сил для третьего положения механизма

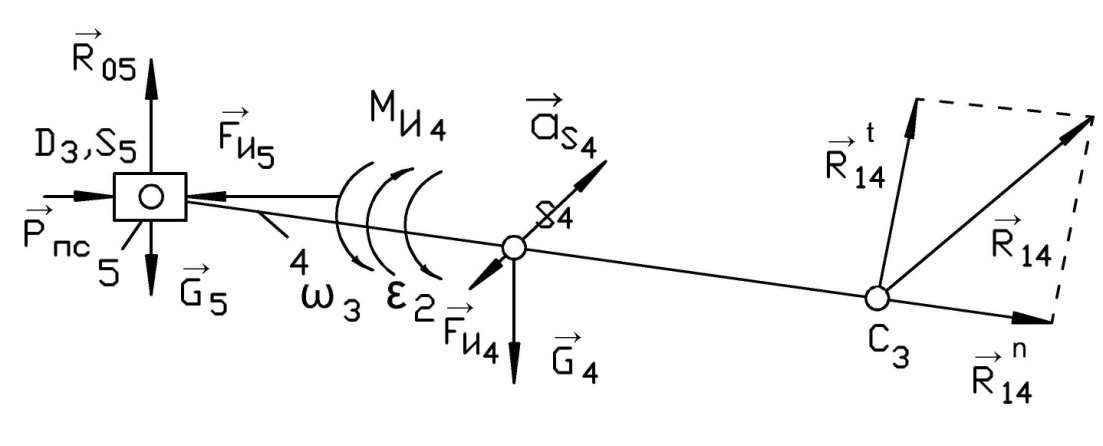
Рисунок 80 - 2 структурная группа с приложенными векторами сил и моментами пар сил для третьего положения механизма

Рисунок 81 – первичный механизм с приложенными векторами сил и моментами пар сил для третьего положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Рисунок 82

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(60)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(61)

(62)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 82 и по формуле (36), м,

Выразим из уравнения (62) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 83 – план сил 1 структурной группы третьего положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 83) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Рисунок 84

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(63)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(64)

(65)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 84 и по формуле (36), м,

Выразим из уравнения (65) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 85 - план сил 2 структурной группы третьего положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 85) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(67)

(68)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 86 .

Рисунок 86

Выразим значение тангенциальной составляющей реакции из формулы (68) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 87).

Рисунок 87 - план сил первичного механизма в третьем положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=28.1247

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для заданного положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для положения 4 (рисунок 88, 89, 90, 91):

Рисунок 88

Рисунок 89 – 1 структурная группа с приложенными векторами сил и моментами пар сил для четвертого положения механизма

Рисунок 90 – 2 структурная группа с приложенными векторами сил и моментами пар сил для четвертого положения механизма

Рисунок 91 – первичный механизм с приложенными векторами сил и моментами пар сил для четвертого положения механизма

Так как структурные группы являются частью структуры механизма, то равновесия не существует. Для его установления используем принцип освобождаемости от связей. Заменим силы реакциями связей.

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна точка ее приложения точка А и линия действия.

Составим уравнения равновесии структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(69)

(70)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 89 и по формуле (36), м,

Выразим из уравнения (70) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 92).

Рисунок 92 – план сил 1 структурной группы четвертого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 92) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(71)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(72)

(73)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 84 и по формуле (36), м,

Выразим из уравнения (73) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 93).

Рисунок 93 - план сил 2 структурной группы четвертого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 93) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(75)

(76)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36).

Выразим значение тангенциальной составляющей реакции из формулы (68) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 87).

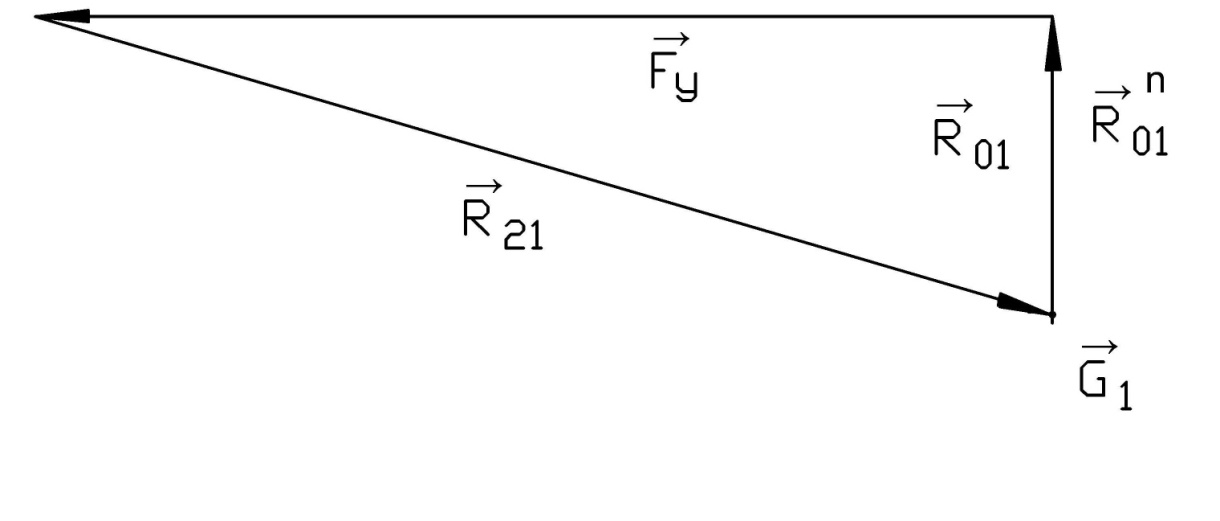
Рисунок 93 - план сил первичного механизма в четвертом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=30.4

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для пятого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 5 положения (рисунки 94, 95, 96, 97):

Рисунок 94

Рисунок 95 – 1 структурная группа с приложенными векторами сил и моментами пар сил для пятого положения механизма

Рисунок 96 - 2 структурная группа с приложенными векторами сил и моментами пар сил для пятого положения механизма

Рисунок 97 – первичный механизм с приложенными векторами сил и моментами пар сил для пятого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(77)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(78)

(79)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 95 и по формуле (36), м,

Выразим из уравнения (79) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 98 – план сил 1 структурной группы пятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 98) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(80)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(81)

(82)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 96 и по формуле (36), м,

Выразим из уравнения (82) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные.

Рисунок 99 - план сил 2 структурной группы пятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 99) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(84)

(85)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 97 .

Выразим значение тангенциальной составляющей реакции из формулы (85) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 100).

Рисунок 100 - план сил первичного механизма в пятом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=29.5972

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для шестого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 6 положения (рисунки 101, 102, 103, 104):

Рисунок 101

Рисунок 102 – 1 структурная группа с приложенными векторами сил и моментами пар сил для шестого положения механизма

Рисунок 103 - 2 структурная группа с приложенными векторами сил и моментами пар сил для шестого положения механизма

Рисунок 104 – первичный механизм с приложенными векторами сил и моментами пар сил для шестого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(86)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(87)

(88)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 102 и по формуле (36), м,

Выразим из уравнения (88) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 105).

Рисунок 105 – план сил 1 структурной группы шестого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 105) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(89)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(90)

(91)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 103 и по формуле (36), м,

Выразим из уравнения (91) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 106).

Рисунок 106 - план сил 2 структурной группы шестого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 106) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(93)

(94)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 104 .

Выразим значение тангенциальной составляющей реакции из формулы (94) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 107).

Рисунок 107 - план сил первичного механизма в шестом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=30.6327

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для седьмого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 7 положения (рисунки 108, 109, 110, 111):

Рисунок 108

Рисунок 109 – 1 структурная группа с приложенными векторами сил и моментами пар сил для седьмого положения механизма

Рисунок 110 - 2 структурная группа с приложенными векторами сил и моментами пар сил для седьмого положения механизма

Рисунок 111 – первичный механизм с приложенными векторами сил и моментами пар сил для седьмого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А.

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(95)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, статическая неопределимость системы 2 - 3 равна 1.

Линии действия векторов сил проходят через полюс - точку B, следовательно,

С помощью плана сил определим оставшиеся неизвестные (рисунок 112).

Рисунок 112 – план сил 1 структурной группы седьмого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C.

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(96)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, статическая неопределимость системы 4 - 5 равна одному.

Линии действия векторов сил проходят через полюс - точку D, следовательно,

С помощью плана сил определим оставшиеся неизвестные (рисунок 113).

Рисунок 113 - план сил 2 структурной группы седьмого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(98)

(99)

Линии действия векторов проходят через полюс – точку А, следовательно:

Выразим значение тангенциальной составляющей реакции из формулы (99) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 114).

Рисунок 114 - план сил первичного механизма в седьмом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=0.4866

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для восьмого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 8 положения (рисунки 115, 116, 117, 118):

Рисунок 115

Рисунок 116 – 1 структурная группа с приложенными векторами сил и моментами пар сил для восьмого положения механизма

Рисунок 117 - 2 структурная группа с приложенными векторами сил и моментами пар сил для восьмого положения механизма

Рисунок 118 – первичный механизм с приложенными векторами сил и моментами пар сил для восьмого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(100)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(101)

(102)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 116 и по формуле (36), м,

Выразим из уравнения (102) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 119).

Рисунок 119 – план сил 1 структурной группы восьмого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 119) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(103)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(104)

(105)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 117 и по формуле (36), м,

Выразим из уравнения (105) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 120).

Рисунок 120 - план сил 2 структурной группы восьмого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 120) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(107)

(108)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 118 .

Выразим значение тангенциальной составляющей реакции из формулы (108) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 121).

Рисунок 121 - план сил первичного механизма в восьмом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=17.1606

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для девятого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 9 положения (рисунки 122, 123, 124, 125):

Рисунок 122

Рисунок 123 – 1 структурная группа с приложенными векторами сил и моментами пар сил для девятого положения механизма

Рисунок 124 - 2 структурная группа с приложенными векторами сил и моментами пар сил для девятого положения механизма

Рисунок 125 – первичный механизм с приложенными векторами сил и моментами пар сил для девятого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(109)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(110)

(111)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 123 и по формуле (36), м,

Выразим из уравнения (111) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 126).

Рисунок 127 – план сил 1 структурной группы девятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 127) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(112)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(113)

(114)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 124 и по формуле (36), м,

Выразим из уравнения (114) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 128).

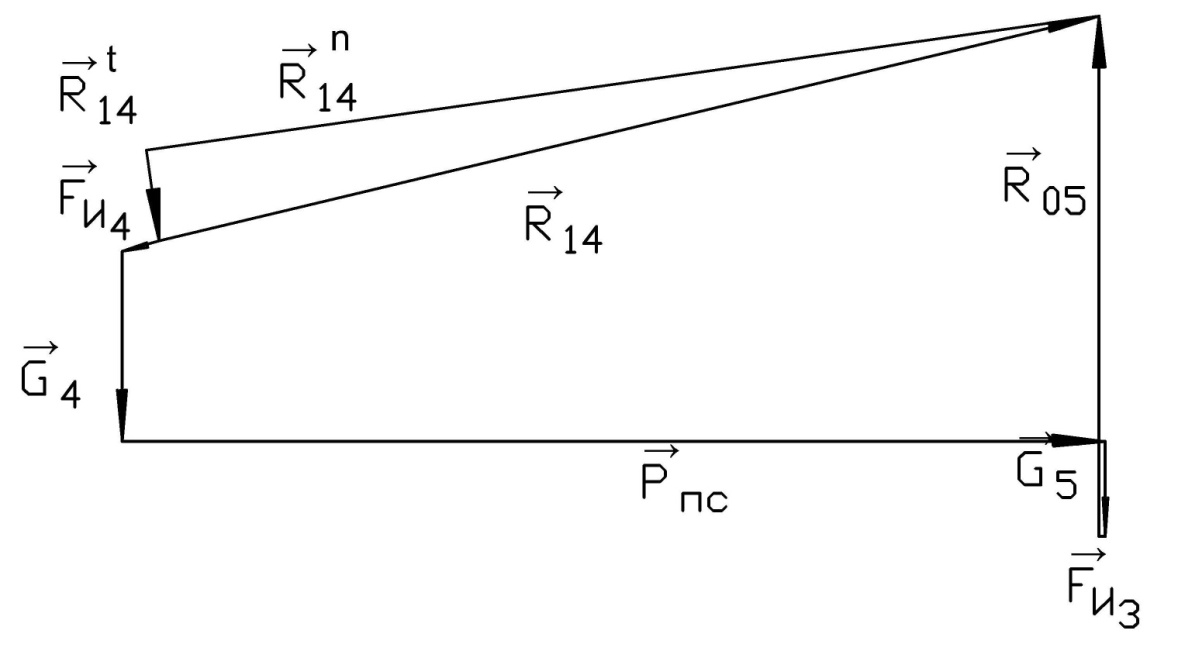
Рисунок 128 - план сил 2 структурной группы девятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 128) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(116)

(117)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 125 .

Выразим значение тангенциальной составляющей реакции из формулы (117) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 129).

Рисунок 129 - план сил первичного механизма в девятом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=25.8438

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для десятого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 10 положения (рисунки 130, 131, 132, 133):

Рисунок 130

Рисунок 131 – 1 структурная группа с приложенными векторами сил и моментами пар сил для десятого положения механизма

Рисунок 132 - 2 структурная группа с приложенными векторами сил и моментами пар сил для десятого положения механизма

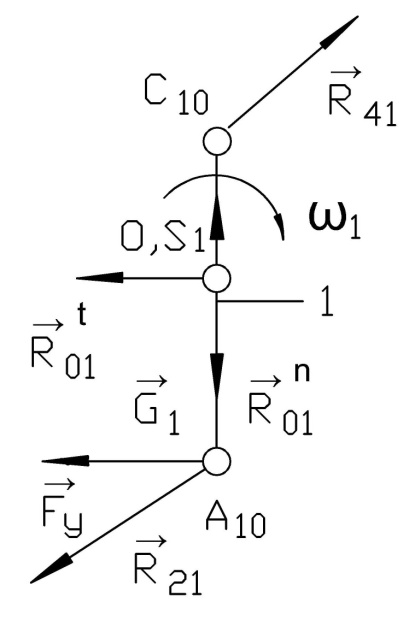
Рисунок 133 – первичный механизм с приложенными векторами сил и моментами пар сил для десятого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(118)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(119)

(120)

Линии действия векторов сил проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 131 и по формуле (36), м,

Выразим из уравнения (120) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 134).

Рисунок 134 – план сил 1 структурной группы десятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 134) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(121)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(122)

(123)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 131 и по формуле (36), м,

Выразим из уравнения (123) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 135).

Рисунок 135 - план сил 2 структурной группы десятого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 135) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(123)

(124)

Линии действия векторов проходят через полюс – точку А, следовательно:

Выразим значение тангенциальной составляющей реакции из формулы (124) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 136).

Рисунок 136 - план сил первичного механизма в десятом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=30.4

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для одиннадцатого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 11 положения (рисунки 137, 138, 139, 140):

Рисунок 137

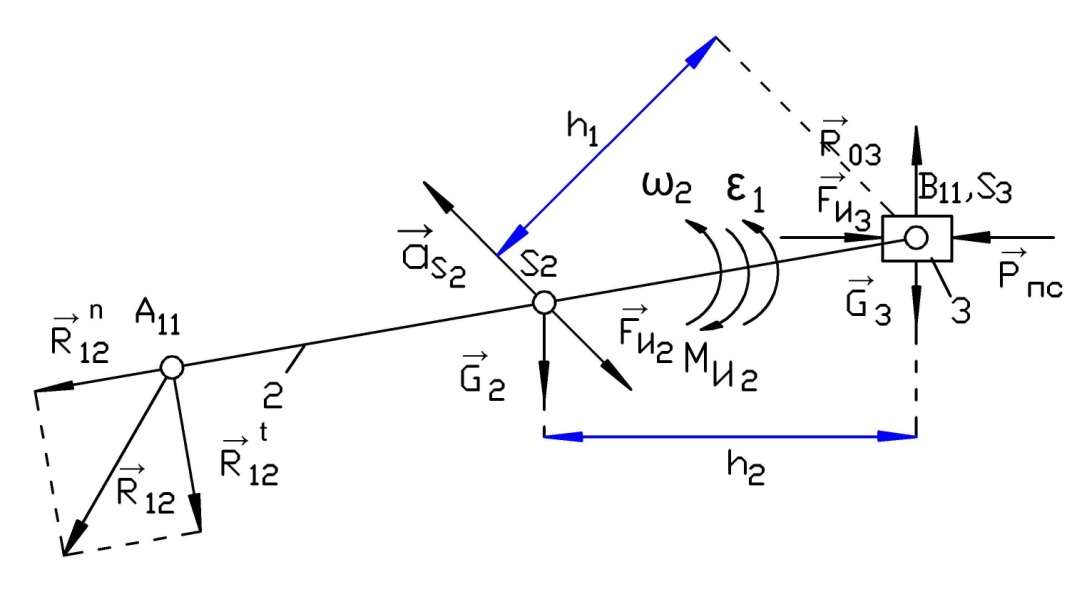
Рисунок 138 – 1 структурная группа с приложенными векторами сил и моментами пар сил для одиннадцатого положения механизма

Рисунок 139- 2 структурная группа с приложенными векторами сил и моментами пар сил для одиннадцатого положения механизма

Рисунок 140 – первичный механизм с приложенными векторами сил и моментами пар сил для одиннадцатого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(125)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(126)

(127)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 138 и по формуле (36), м,

Выразим из уравнения (127) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 141).

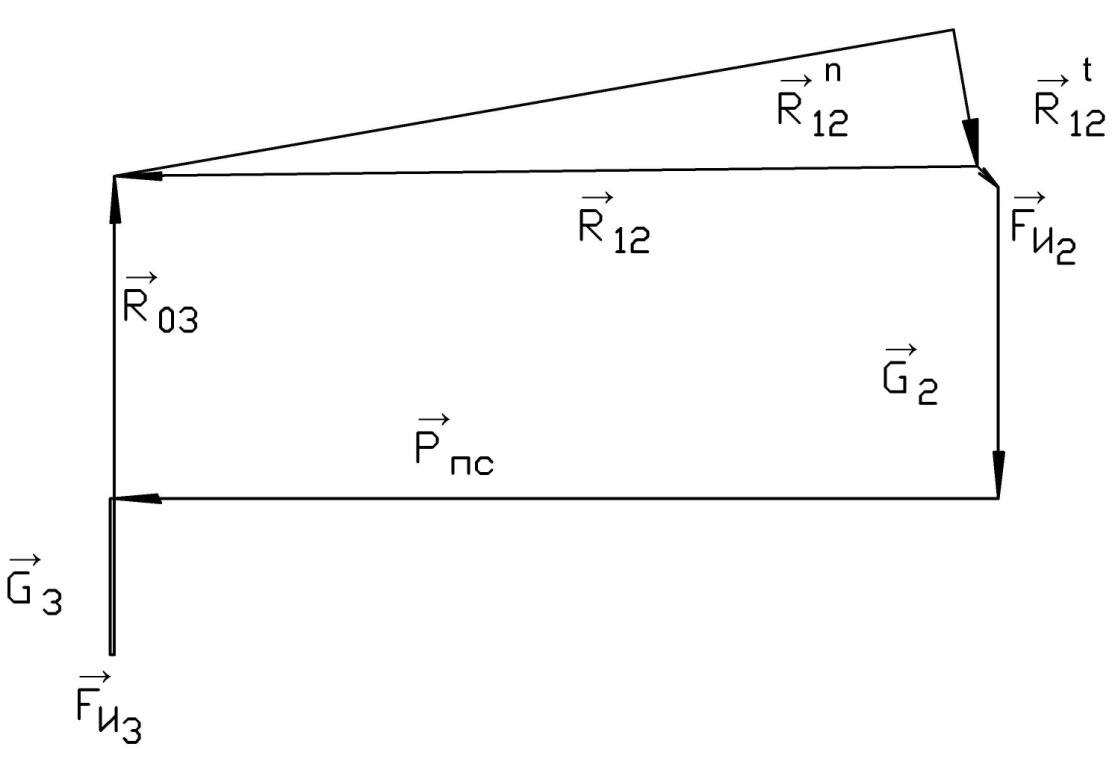
Рисунок 141 – план сил 1 структурной группы одиннадцатого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 141) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(128)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(129)

(130)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 139 и по формуле (36), м,

Выразим из уравнения (130) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 142).

Рисунок 142 - план сил 2 структурной группы одиннадцатого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 142) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(132)

(133)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 140 .

Выразим значение тангенциальной составляющей реакции из формулы (133) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 143).

Рисунок 144 - план сил первичного механизма в одиннадцатом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=25.894

Согласно составу структуры плоского рычажного механизма вычертим в масштабном коэффициенте длин структурные группы звеньев и первичный механизм для двенадцатого положения ведущего звена.

Приложим к звеньям структурных групп и первичного механизма вектора сил и моменты пар сил, сохраняя их направление и линии действия согласно расчетной схемы механизма для 12 положения (рисунки 145, 146, 147, 148):

Рисунок 145

Рисунок 146 – 1 структурная группа с приложенными векторами сил и моментами пар сил для двенадцатого положения механизма

Рисунок 147 - 2 структурная группа с приложенными векторами сил и моментами пар сил для двенадцатого положения механизма

Рисунок 148 – первичный механизм с приложенными векторами сил и моментами пар сил для двенадцатого положения механизма

Структурная группа звеньев 2 – 3. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОВ). Для реакции известна только точка ее приложения точка А. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 2-3.

Для структурной группы звеньев 2 – 3 Уравнение равновесия полученной системы принимает вид:

(134)

Уравнение равновесия для структурной группы звеньев 2 – 3 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 2 - 3 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(135)

(136)

Линии действия векторов сил , проходят через полюс - точку B, следовательно,

Плечи моментов найдем из рисунка 146 и по формуле (36), м,

Выразим из уравнения (136) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 2 – 3 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 149).

Рисунок 149 – план сил 1 структурной группы двенадцатого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 149) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 4 – 5. Действующими силовыми факторами являются: силы тяжести звеньев и , силы инерции и , момент пары сил инерции , реакции и . Для реакции известна точка ее приложения и линия действия (перпендикулярно к прямой ОD). Для реакции известна только точка ее приложения точка C. Разложим вектор на две составляющие .

Составим уравнения равновесия структурной группы 4-5.

Для структурной группы звеньев 4 – 5 уравнение равновесия полученной системы принимает вид:

(137)

Уравнение равновесия для структурной группы звеньев 4 – 5 содержит

три неизвестных: , .

Статическая неопределимость определяется по формуле (44):

Следовательно, система 4 - 5 дважды статически неопределима.

С целью раскрытия статической неопределимости найдем значение тангенциальной составляющей реакции

(138)

(139)

Линии действия векторов сил , проходят через полюс - точку D, следовательно,

Плечи моментов найдем из рисунка 147 и по формуле (36), м,

Выразим из уравнения (139) значение тангенциальной составляющей реакции и найдем это значение, H,

Знак «-»означает, что реальное направление действия реакции противоположно изначально предполагаемому нами направлению действия данного вектора поэтому учтем это на плане сил.

В уравнении равновесия для структурной группы звеньев 4 – 5 осталось две неизвестные – это , . Статическая неопределимость равна одному. С помощью плана сил определим оставшиеся неизвестные (рисунок 150).

Рисунок 150 - план сил 2 структурной группы двенадцатого положения механизма

Масштабный коэффициент равен:

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

Измерив на плане сил (рисунок 150) значение реакции связи и подставив это значение в формулу (46), найдем реакцию связи, Н,

Структурная группа звеньев 1 – 0. Действующими силовыми факторами являются: сила тяжести кривошипа 1 , реакция в шарнире A ( , реакция . Для реакции известна только точка приложения - точка O. Разложим реакцию . на составляющие и .

Равнодействующую силу прикладываем к точке A и направляем произвольно. Полученная система плоских сил находится в состоянии кинетостатического равновесия.

Составим уравнения равновесия первичного механизма.

Для структурной группы звеньев 1 – 0 уравнение равновесия полученной системы принимает вид:

Уравнение равновесия для структурной группы звеньев 1 – 0 содержит три неизвестных:

Подставим значение коэффициентов в формулу (44):

Следовательно, статическая неопределимость системы 1 - 0 равна двум.

Найдем значение тангенциальной составляющей реакции . составив сумму моментов всех сил, действующих на первичный механизм 1 – 0 относительно полюса A для звена 1:

(141)

(142)

Линии действия векторов проходят через полюс – точку А, следовательно:

Плечо момента найдем по формуле (36) и рисунку 148 .

Выразим значение тангенциальной составляющей реакции из формулы (142) и найдем это значение, H,

В уравнении равновесия для структурной группы звеньев 1 – 0 осталось 2 неизвестных – это , статическая неопределимость равна одному.

С помощью плана сил определим оставшиеся неизвестные (рисунок 151).

Рисунок 151 - план сил первичного механизма в одиннадцатом положении

Переведем силы в масштабный коэффициент, подставим значение коэффициентов в формулу (46), мм,

=

= · 0.16=27.1578