Стандартная форма задачи лп

Cтандартная форма применяется для геометрической интерпритации. Стандартной модель - все функциональные ограничения имеют вид неравенств и все переменные неотрицательные. Тип экстремума не имеет существенного значения.

Таким образом, стандатрная форма модели имеет вид

Векторно-матричных обозначения:L = max

или

Число переменных при отсутствии неограниченных по знаку переменных не больше Матрица и вектор имеют меньшие размеры, чем в канон. модели.

Преобразование равенств в неравенства. Пусть в исходной модели имеется q равенств. Решив эту систему уравнений относительно первых q переменных, получим

Используя эти равенства, исключаем из целевой функции и ограничений, уменьшая тем самым количество переменных на q. Однако число ограничений не изменяется, так как для сохранения неотрицательности исключенных переменных должны выполняться неравенства

Таким образом, все ограничения задачи будут записаны в виде неравенств.

9. Основные понятия лп, свойства задач лп. Постановка задачи

Задача, модель которой содержит только линейные функции искомых переменных, - задача линейного программирования (ЛП). В общем случае:

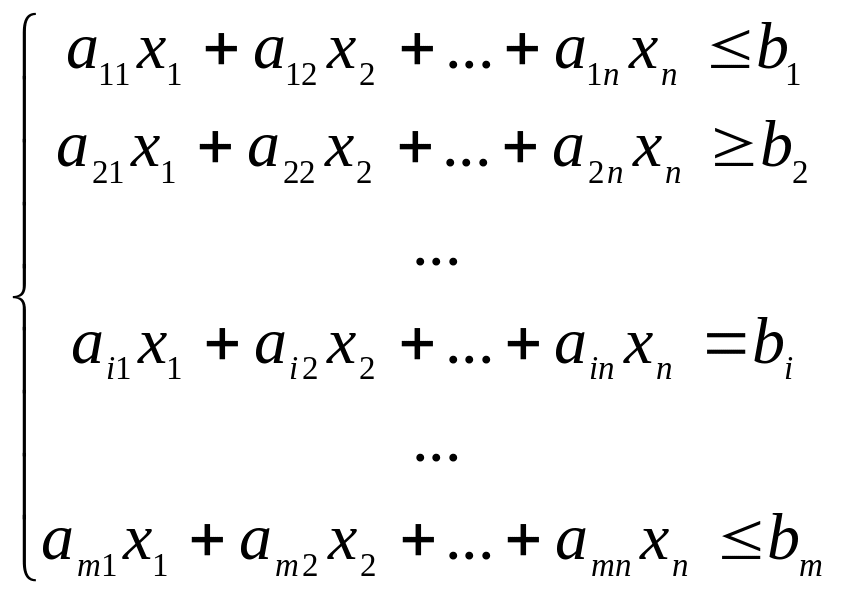
где L – критерий (целевая функция); n - количество переменных;

C_i – параметры (коэффициенты) критерия, не все C_i =0;

– параметры условий (могут быть любыми действительными числами, но одновременно все не могут равняться нулю при i=const).

b_i – параметры (свободные члены), отражающие возможности по ресурсам, допустимые/требуемые значения показателей (любые действительные числа).

На часть или все переменные накладывается условие неотрицательности.

Задача состоит в определении таких значений переменных, удовлетворяющих условиям, которые доставляют максимум/ минимум линейной форме.

Основные понятия лп. Свойства задач лп

Множество D={xRⁿ| AXB, X0} - допустимое множество задач ЛП; это множество всех решений, удовлетворяющих всем ограничениям задачи. Любое решение ХD - допустимое решение задачи ЛП. Допустимое решение Х^* является оптимальным для задачи максимизации, если выполняется неравенство

L(X^*)  L(X), XD.

Множество называется замкнутым, если оно содержит и свою границу, в противном случае оно открытое. Множество может быть ограниченным, если на нем все переменные ограничены снизу и сверху, и неограниченным, если хотя бы одна переменная на нем не ограничена. Непрерывное множество выпукло, если вместе с любыми двумя точками оно содержит и весь соединяющий их отрезок, иначе множество будет невыпуклым.

Пусть условия задачи записаны в стандартной форме

a_ijx_j b_i,

Так как в условия входят только непрерывные переменные, а отношения являются нестрогими, то порождаемое ими множество непрерывно и замкнуто. Возьмем одно неравенство. При двух переменных граница области, где выполняется это неравенство, представляет собой прямую, а множество значений переменных, удовлетворяющих строгому неравенству, расположено с одной стороны границы. Таким образом, неравенству соответствует полуплоскость, которая является выпуклым множеством. При трех переменных границей будет плоскость, а соответствующее множество – выпуклым полупространством. При большем числе переменных неравенство порождает многомерное выпуклое полупространство с границей – гиперплоскостью.

Пересечение выпуклых множеств выпукло (если оно не пустое). В задаче ЛП число неравенств, а, значит, число полупространств, конечно. Их пересечение и дает допустимое множество D.

Пересечение конечного числа выпуклых полупространств, если оно не пустое, называется выпуклым многогранным множеством.

Ограниченное выпуклое многогранное множество называется выпуклым многогранником (пример : пирамиды, призмы).

Таким образом, допустимое множество задачи ЛП может быть или выпуклым многогранным множеством, или выпуклым многогранником, или пустым. Других вариантов быть не может.

Критерий L=C_jX_j – линейная функция и поэтому удовлетворяет условиям как выпуклости, так и и вогнутости одновременно.

Максимум вогнутой функции или минимум выпуклой функции на выпуклом множестве может достигаться только на границе.

Аналогичный вывод следует из рассмотрения критических точек целевой функции. Так как производная

= Const,

то точек, в которых она равна нулю или терпит разрыв, нет. Поэтому, если оптимум существует, то он может быть только на границе.

Задача ЛП называется разрешимой, если она имеет хотя бы одно оптимальное решение, и неразрешимой в противном случае.

При решении задач ЛП возможны только три случая:

1. Условия задачи противоречивы (несовместны), допустимое множество пустое и, следовательно, задача неразрешима.

2. Условия задачи совместны, но допустимое множество неограниченно. Тогда возможны два исхода:

а) если критерий неограничен на этом множестве, то задача неразрешима;

б) если критерий ограничен, то задача разрешима.

3. Условия непротиворечивы и множество является выпуклым многогранником. В этом случае задача всегда разрешима.

Следует, что причиной неразрешимости задачи ЛП может быть либо неограниченность критерия, либо противоречивость ограничений.