45. Генетические алгоритмы

По своей концепции генетические алгоритмы близки к методам случайного поиска. В них сочетаются элементы случайности и детерминированности, что характерно для всех природных процессов. Заимствованием механизмов живой природы и обусловлено название "генетические". Детерминированная составляющая алгоритмов в большей степени представлена в моделировании процессов отбора, размножения и наследования, а случайная – процесса мутации.

Любая альтернатива (вариант) представляется в виде строки (как правило, битовой) фиксированной длины, с которой манипулируют вне связи с содержанием задачи. Строка называется кодом. В коде в общем случае представлен набор параметров, зависящих от аргументов целевой функции. Код и его структура определяют генотип. Экземпляры кода - хромосомы / особи, есть точки в пространстве поиска. Совокупность особей образует популяцию, а последовательные популяции – поколения. Основными параметрами конкретного алгоритма являются размер популяции и вероятности применения операторов. Первоначально по содержанию задачи формируется генотип и создается исходная популяция. Размер популяции N рекомендуется брать исходя из оценки числа возможных альтернатив r: К текущей популяции применяется оператор отбора, в результате чего образуется множество родительских пар. При максимизации целевой функции вероятность особи стать родителем может вычисляться по формуле

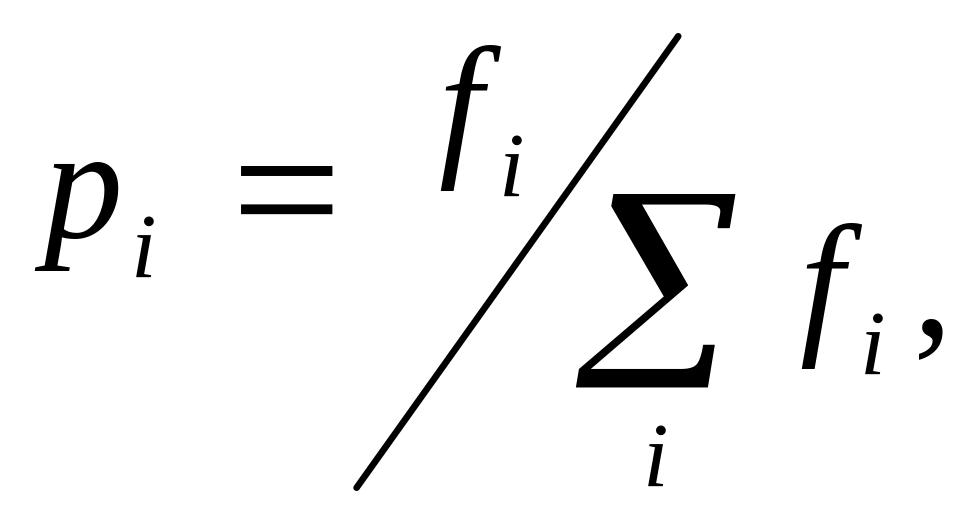где f_i – значение критерия на i-й особи.

Д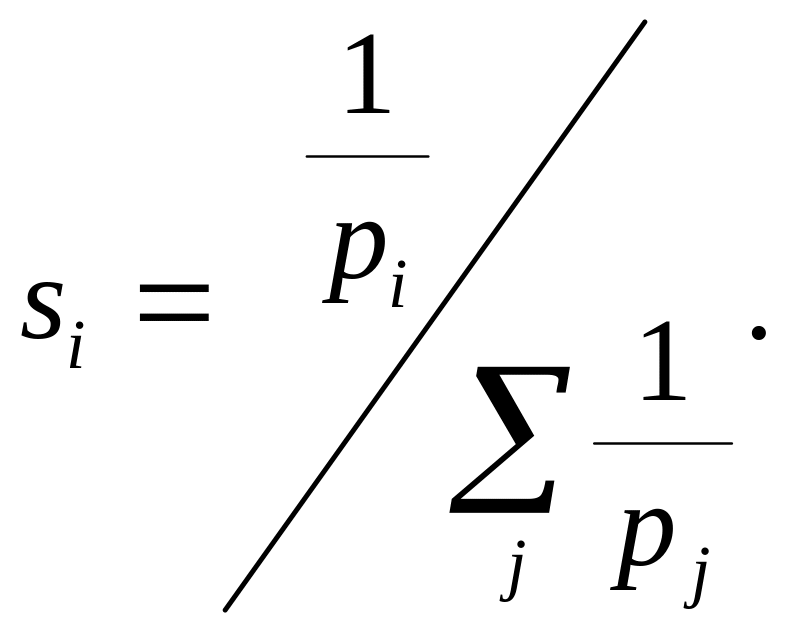 ля создания потомков используется оператор скрещивания, моделирующий процесс наследования за счет передачи части свойств от родителей к потомкам. Вероятность его применения рекомендуется брать не ниже 0,9. Он производит обмен подстроками родительских особей, от пары родителей образуется два потомка. Как это происходит, зависит от выбранной процедуры скрещивания. Например, при длине строки n из первых n-1 равновероятных натуральных чисел разыгрывается одно число, которое принимается за точку разбиения. Затем подстроки родителей, находящиеся справа от точки разбиения, меняются местами. К новым особям применяется оператор мутации. Вместе с оператором скрещивания он позволяет расширить область поиска, получить особи со свойствами, отсутствующими у родителей. Вероятность мутации берется не выше 0,01. Процесс мутации заключается в случайной перестановке 2 элементов строки, в смене значения случайного элемента строки с 0 на 1 или наоборот, в циклическом сдвиге элементов строки и т.п. Добавление потомков приводит к расширению популяции. В алгоритмах стационарного состояния все поколения имеют одинаковый размер. Поэтому на следующем шаге алгоритма производится сокращение популяции оператором редукции. Вероятность его применения к особи м определить через вероятность отбора p_i:

На последнем шаге цикла проверяется условие останова. В качестве критерия останова используют число поколений, качество поколения (пороговое значение), близость особей между собой и др.

Для повышения эффективности генетических алгоритмов предлагаются способы распараллеливания вычислений, сокращения размера популяции за счет выделения кластеров и замены каждого одной особью, разрабатываются алгоритмы с изменяемым размером популяции.

Отличительной чертой генетических алгоритмов является одновременное использование набора точек в пространстве поиска вместо перехода от точки к точке в традиционных методах. Эта особенность позволяет применять такие алгоритмы для решения многоэкстремальных задач.

Самым важным этапом применения алгоритма является определение генотипа (структуры кода) и для каждой задачи он индивидуален. Кроме того, специфика задачи может диктовать и требования к работе операторов. Например, в задаче коммивояжера оператор скрещивания не должен порождать потомков, в коде которых один пункт представлен более одного раза.