Правило северо-западного угла

	b1	b2	…	bn
	C11 X11	C12 X12	…	C1n X1n
	C21 X21	C22 X22	…	C2n X2n
…	…	…	…	…
	Cm1 Xm1	Cm2 Xm2	…	Cmn Xmn

Все исходные данные и переменные сбалансированной Т-задачи удобно представить в виде таблицы. Построение плана начинается с северо-западной клетки таблицы, то есть первым определяется значение переменной X₁₁. Так как оно должно быть максимально допустимым, то Обязательно выполнится одно из равенств ПО, ПН, что соответствует закрытию строки или столбца: переменные в остальных клетках строки или столбца будут равны нулю. Если X₁₁=а₁, то закрывается первая строка, следующей базисной переменной будет X₂₁. X₂₁=min(a₂, b₁-a₁). Если X₁₁=b₁, то закроется первый столбец и следующей базисной переменной станет X₁₂=min(a₁-b₁, b₂).

П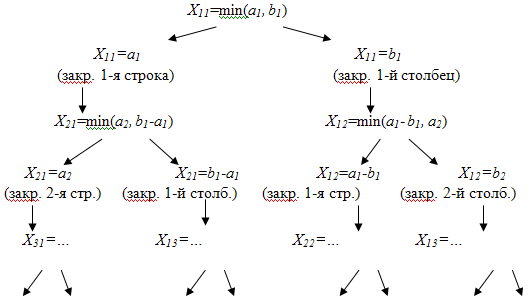 роцесс построения начального плана м представить в виде след. дерева решений.

Общее правило определения значения очередной базисной переменной: X_ij=min(ост от a_i, ост от b_j). На каждом шаге закрывается или строка, или столбец, а на последнем шаге при назначении X_mn закрываются одновременно m-я строка и n-й столбец (так как задача сбалансированная). Таким образом, число базисных переменных равно m+ n-1. Построение начального плана завершено.

ПО	Потребитель (ПН)				Запасы груза
	B1	B2	B3	B4
A1	6 75	7 25	3	5	100
A2	1	2 55	5 60	6 35	150
A3	3	10	20	1 50	50
Потр-ть	75	80	60	85	300

Пример: Исходные данные и построение начального плана показано в табл. Порядок движения по клеткам отражен стрелками. Этому плану соответствуют суммарные затраты L=1295.

Правило минимального элемента.

В приведенном способе построения плана не участвовали затраты на перевозку. Учет затрат позволит получить начальный план, более близкий к оптимальному. Первой заполняется клетка с минимальными затратами. Пусть minC_ij=C_kp. Тогда X_kp=min(a_k, b_p). Если при этом закрывается строка

ПО	Потребитель(ПН)				Запасы груза
	B1	B2	B3	B4
A1	6	7 5	3 60	5 35	100
A2	1 75	2 75	5	6	150
A3	3	10	20	1 50	50
Потр-ть	75	80	60	85	300

k, то в столбце p ищем клетку с минимальными затратами и определяем значение соответствующей переменной. При закрытии столбца p действуем аналогично в строке k. В общем случае клетка, лежащая в закрытом столбце и/или закрытой строке является закрытой, иначе – открытой. На каждом шаге движение идет либо по столбцу, либо по строке и при этом отыскивается среди открытых клетка с минимальным значением C_ij.

Пример: Построим начальный план по правилу минимального элемента для задачи из примера 1. Результат в табл.

При таком начальном плане L=665, что меньше чем в примере 1. Однако нельзя утверждать, что для любых данных этот способ дает лучший план. Правило минимального элемента эффективнее в среднем (на множестве задач). В то же время алгоритм реализации этого правила сложнее, чем правила северо-западного угла.

Применяется также вариант, в котором на каждом шаге ищется клетка с минимальными затратами среди всех открытых клеток. Такой способ еще сложнее, но в среднем дает планы, более близкие к оптимальным.