
- •1. Основные понятия и этапы са. Основные понятия са
- •Этапы системного анализа
- •2. Операция и ее составляющие. Этапы ио.
- •3. Применение научных методов Этапы операционного проекта
- •6. Внедрение результатов исследования.
- •3. Виды математических моделей ио, примеры.
- •4. Состязательные задачи. Решение игры 2-х лиц.
- •5. Классификация и характеристики смо. Понятие системы массового обслуживания
- •Поток событий и его свойства
- •Транспортная задача
- •8. Формы представления задач лп и способы приведения к ним. Каноническая форма задач лп
- •Стандартная форма задачи лп
- •9. Основные понятия лп, свойства задач лп. Постановка задачи
- •Основные понятия лп. Свойства задач лп
- •10. Геометрия задач лп, базисные решения, вырожденность. Геометрия задач лп
- •Выделение вершин допустимого множества
- •11. Понятие базиса, переход от одного базисного решения к другому.
- •Построение начального базисного решения
- •13. Алгоритм симплекс-метода.
- •14. Двойственность в лп, построение моделей двойственных задач. Двойственность задач лп
- •Запись двойственной задачи в симметричном случае
- •Запись двойственной задачи в общем случае
- •15. Экономическая интерпретация двойственной задачи. Двойственный симплекс-метод. Интерпретация двойственной задачи
- •Двойственный симплекс-метод
- •16. Теоремы двойственности.
- •17. Учет двусторонних ограничений, модифицир. Симплекс-метод. Учет двусторонних ограничений
- •М одифицированный алгоритм
- •18. Параметрический анализ вектора ограничений.
- •19. Параметрический анализ коэффициентов линейной формы.
- •20. Модели транспортных задач и их хар-ка, условия разрешимости. Простейшая транспортная задача (т-задача)
- •Транспортная задача с ограниченными пропускными способностями (Td - задача)
- •Многоиндексные задачи
- •Транспортные задачи по критерию времени
- •21. Построение начального плана перевозок т-задачи
- •Правило северо-западного угла
- •Правило минимального элемента.
- •Метод Фогеля
- •22. Обоснование метода потенциалов. Переход от одного плана перевозок к другому
- •Признак оптимальности
- •23. Алгоритм метода потенциалов
- •24. Двойственность т-задач, эконом. Интерпретация потенциалов. Двойственная пара транспортных задач
- •Экономическая интерпретация потенциалов
- •25. Метод потенциалов для Td-задачи.
- •26. Приведение открытой модели транспортной задачи к закрытой.
- •27. Трансп. Задачи в сетевой постановке, задача о кратчайшем пути. Транспортные задачи в сетевой постановке (транспортные сети)
- •Алгоритм Дейкстры-Форда:
- •28. Задача о максимальном потоке.
- •29. Метод декомпозиции Данцига-Вулфа в общем случае.
- •30. Метод декомпозиции транспортных задач
- •31. Постановка задач стохастического программирования
- •32. Целочисленное программирование: Особенности, концепции точных и приближенных методов решений.
- •Проблема целочисленности
- •33. Методы отсечений.
- •34. Метод ветвей и границ.
- •35. Аддитивный метод.
- •36. Нелинейное программирование (нлп): постановка, классы задач нлп, условия оптимальности. Характеристика задач
- •Условия оптимальности
- •37. Квадратичное программирование.
- •38. Сепарабельное и дробно-линейное программирование. Сепарабельное программирование (сп)
- •Задачи дробно-линейного программирования
- •39. Методы покоординатного спуска и Хука-Дживса. Метод Гаусса-Зейделя (покоординатного спуска)
- •Метод Хука-Дживса (метод конфигураций)
- •40. Симплексный метод поиска.
- •41. Градиентные методы.
- •Методы сопряженных направлений
- •Методы Пауэла, Флетчера-Ривса, Девидона-Флетчера-Пауэла
- •43. Методы случайного поиска.
- •Алгоритм с возвратом при неудачном шаге
- •Алгоритм с обратным шагом
- •Алгоритм наилучшей пробы
- •Алгоритм статистического градиента
- •44. Метод проектирования градиентов.
- •45. Генетические алгоритмы
- •46. Методы штрафных и барьерных функций. Метод штрафных функций
- •Метод барьерных функций
- •47. Динамическое программирование (дп): принцип оптимальности, функциональное уравнение, процедура дп.
- •Как работает метод дп
- •Функциональное уравнение дп
- •48. Дп: задача распределения ресурсов, достоинства дп.
- •49. Дп: задача о кратчайшем пути и с мультипликативным критерием. Задача о кратчайшем пути
- •Задача с мультипликативным критерием
- •50. Дп: организация выпуска m видов продукции.
- •51. Дп: задача об инвестициях.
- •52. Дп: многомерные задачи и проблемы решения.
- •53. Дп: снижение размерности с помощью множителей Лагранжа
- •54. Задачи спу: построение сети и временной анализ.
- •Временной анализ (для детерминированной сети)
- •55. Задачи спу: оптимизация.
- •56. Многокритериальные задачи: постановка, проблемы, основные понятия, методы.
- •Методы многокритериальной оптимизации
- •57. Многокрит. Задачи: функция полезности, лексикографический метод. Функция полезности
- •Решение на основе лексикографического упорядочения критериев
- •58. Методы главного критерия, свертки, идеальной точки, целевого програм-я. Метод главного критерия
- •Линейная свертка
- •Метод идеальной точки
- •Целевое программирование (цп)
- •59. Диалоговые методы решения задач по многим критериям.
- •Метод уступок
- •Интерактивное компромиссное программирование
16. Теоремы двойственности.
Между решениями прямой и двойственной задач существует связь (позволяет по решению одной задачи двойственной пары получать решение другой), которая устанавливается теоремами двойственности. Рассмотрим составляющие теоремы.
Теорема 1. Если в оптимальном решении
прямой задачи условие выполняется как
строгое неравенство
![]() ,
то соответствующая двойственная
переменная равна нулю, то есть
,
то соответствующая двойственная
переменная равна нулю, то есть
![]() Обоснование:
Неравенство означает, что i-й
ресурс используется не полностью,
следовательно, малое изменение этого
ресурса не повлияет на результат
деятельности (критерий) и поэтому
значение двойственной переменной равно
нулю.
Обоснование:
Неравенство означает, что i-й
ресурс используется не полностью,
следовательно, малое изменение этого
ресурса не повлияет на результат
деятельности (критерий) и поэтому
значение двойственной переменной равно
нулю.
Следствие. Если дополнительная переменная в i-м условии прямой задачи больше нуля, то соответствующая двойственная переменная равна нулю.
Теорема 2. Если в единственном
оптимальном решении прямой задачи
условие выполняется как равенство
![]() то
соответствующая двойственная переменная
будет заведомо не равна нулю. Равенство
означает, что i-й
ресурс полностью исчерпан, следовательно,
малые изменения этого ресурса обязательно
приведут к изменению критерия и поэтому
его значимость не равна нулю.
то
соответствующая двойственная переменная
будет заведомо не равна нулю. Равенство
означает, что i-й
ресурс полностью исчерпан, следовательно,
малые изменения этого ресурса обязательно
приведут к изменению критерия и поэтому
его значимость не равна нулю.
С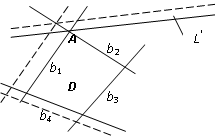 ледствие.
Если дополнительная переменная в i-м
условии равна нулю, то двойственная
переменная этого условия не равна нулю.
ледствие.
Если дополнительная переменная в i-м
условии равна нулю, то двойственная
переменная этого условия не равна нулю.
На рис. приведена геометрическая интерпретация рассмотренных теорем для случая единственного оптимального решения (вершина А). Множество D образовано четырьмя условиями- неравенствами с ресурсами b1, b2, b3 и b4. В оптимальном решении по 1-му и 2-му ресурсам выполняется равенство и изменение любого из них (показано пунктиром для b1) приводит к перемещению оптимальной вершины и, следовательно, критерия. Поэтому значимость этих ресурсов или их двойственные переменные отличны от нуля. В то же время по 3-му и 4-му ресурсам имеем строгие неравенства и их изменения не влияют на оптимальное значение критерия, что соответствует нулевым дополнительным переменным.
С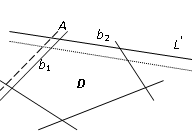 лучай
с неединственным оптимальным решением:
Линия оптимального значения критерия
L* совпадает
с границей по 2-му ресурсу. В оптимальном
решении, соответствующем вершине А,
первые два ресурса используются
полностью. Однако изменение b1
не приводит к изменению критерия, тогда
как любое изменение b2
отражается на оптимальном значении
критерия. Поэтому оценки этих ресурсов
разные: U1=0,
U20.
лучай
с неединственным оптимальным решением:
Линия оптимального значения критерия
L* совпадает
с границей по 2-му ресурсу. В оптимальном
решении, соответствующем вершине А,
первые два ресурса используются
полностью. Однако изменение b1
не приводит к изменению критерия, тогда
как любое изменение b2
отражается на оптимальном значении
критерия. Поэтому оценки этих ресурсов
разные: U1=0,
U20.
Теорема
![]() .
Если в оптимальном решении двойственной
задачи условие выполняется как строгое
неравенство
.
Если в оптимальном решении двойственной
задачи условие выполняется как строгое
неравенство
![]() то соответствующая переменная прямой
задачи равна нулю:
то соответствующая переменная прямой
задачи равна нулю:
![]() Интерпретация: если затраты превышают
производимую стоимость, то производить
такую продукцию невыгодно.
Интерпретация: если затраты превышают
производимую стоимость, то производить
такую продукцию невыгодно.
Т еорема
еорема![]() Если в единственном оптимальном
решении двойственной задачи условие
выполняется как равенство, то
соответствующая переменная прямой
задачи строго больше нуля:
Если в единственном оптимальном
решении двойственной задачи условие
выполняется как равенство, то
соответствующая переменная прямой
задачи строго больше нуля:
![]() .
Так как производимая стоимость равна
затратам, то производство такой продукции
окупается.
.
Так как производимая стоимость равна
затратам, то производство такой продукции
окупается.
Обобщение: вторая основная теорема двойственности: Для того чтобы векторы X* и U* являлись оптимальными решениями прямой и двойств. задач соответственно, необходимо и достаточно выполнение след. условий:
Пример
ПЗ L=7x1+5x2→max, 2x1+3x219, 2x1+x213, 3x212, 3x117, x10, x20 |
Кан. форма ПЗ L=7x1+5x2→max, 2x1+3x2+x3=19, 2x1+x2+ x4=13, 3x2+x5=12, 3x1+x6=17, xj0.
|
Оптимальное решение
|
ДЗ =19U1+13U2+12U3+17U4min 2U1+2U2+3U47 3U1+U2+3U35 Ui 0 |
Получим решение ДЗ на основе решения ПЗ и теорем двойственности.
Тк дополнительные переменные х5
и х6, входящие в 3 и 4 условия
ПЗ, в оптимальном решении не равны нулю,
то согласно следствию теоремы 1
![]() .
.
И
![]() з
первой группы условий следует, что если
исходная переменная ПЗ не равна нулю,
то ограничение ДЗ будет выполняться
как равенство. Поэтому:
з
первой группы условий следует, что если
исходная переменная ПЗ не равна нулю,
то ограничение ДЗ будет выполняться
как равенство. Поэтому:
Получили систему 2-х уравнений с двумя неизвестными. Ее решение:
![]() .
.
Т.о, мы нашли решение ДЗ без применения симплекс-метода. Пример демонстрирует связь решений двойственной пары задач, а значения двойственных переменных легко получить из оптимальной симплекс-таблицы ПЗ. Они расположены в вспомогательной строке Z в столбцах начального базиса.
Теорема 3. Если X
и U – допустимые
решения прямой и двойственной задач
соответственно, то L(X)
(U).
Доказательство. Так как допустимость
решений означает выполнение неравенств
![]() в ПЗ и
в ПЗ и
![]() в
ДЗ, то очевидна цепочка соотношений
в
ДЗ, то очевидна цепочка соотношений
![]()
из которой следует справедливость теоремы.
Теорема 4. Если X* и U* - допустимые решения прямой и двойственной задач и L(X*)= (U*), то они являются оптимальными решениями двойственной пары задач.
Доказательство. Согласно теореме 3 для любого допустимого X справедливо неравенство L(X) (U*). И так как L(X*)= (U*) по условию теоремы, то L(X)L(X*). Следовательно, X*- оптимальное решение прямой задачи по определению.
Аналогично доказывается оптимальность U* для двойственной задачи.
Т еорема
5. Для любых оптимальных X*
и U* линейные
формы прямой и двойственной задач равны:
L(X*)=
(U*).
Доказательство. В оптимальных решениях
выполняются равенства т 3. Суммируя
первую группу по j
, а вторую по i:
еорема
5. Для любых оптимальных X*
и U* линейные
формы прямой и двойственной задач равны:
L(X*)=
(U*).
Доказательство. В оптимальных решениях
выполняются равенства т 3. Суммируя
первую группу по j
, а вторую по i:
Из равенства левых частей следует равенство правых и, значит, справедливость теоремы.
Теорема 6. Если линейная форма одной из задач двойственной пары не ограничена, то условия другой противоречивы. (Обратное не всегда верно, возможна противоречивость в обеих задачах). Доказательство противного. Допустим, что при неограниченности L(x) сверху в прямой задаче условия двойственной задачи непротиворечивы. Тогда существует допустимое решение ДЗ, на котором. значение ее критерия конечно. Но согласно теореме 3 для допустимых решений должно выполняться неравенство L(x) (U), что при принятом допущении невозможно (L бесконечно, а конечно). Следовательно, ДЗ не может иметь допустимых решений, то есть ее условия противоречивы. Аналогично доказывается 2-я часть теоремы для случая неограниченности снизу .
Обобщение: первая основная теорема двойственности: Если одна из задач двойственной пары разрешима, то и другая задача разрешима, при этом оптимальные значения критериев равны; при неразрешимости одной из задач другая тоже неразрешима.
