15. Экономическая интерпретация двойственной задачи. Двойственный симплекс-метод. Интерпретация двойственной задачи

Д войственная модель дает возможность оценить решение исходной задачи. В примере прямая задача состоит в наилучшем использовании всех имеющихся ресурсов. Каждому варианту плана производства продукции соответствует свое использование ресурсов, а, следовательно, и их полезность (степень влияния ресурса на результат). Тк каждому условию прямой задачи, отражающему использование ресурса, ставится в соответствие двойственная переменная, то она - мерило значимости этого ресурса.

Рассмотрим уравнение условия двойственной задачи [A][U]=[C].

Пусть ресурс –сколько часов оборудование может быть загружено в течение планового периода. Тогда размерность двойственной переменной будет:

Итак, U дает стоимость единицы ресурса в единицах критерия, то есть прирост произведенной стоимости в рублях на каждый дополнительный час работы оборудования. Поэтому двойственные переменные называют теневыми ценами. Т.о, чем больше абсолютная величина двойственной переменной, тем выше значимость ресурса в полученном решении, и наоборот, более сильному влиянию ресурса на критерий соответствует большее значение двойственной переменной.

Теперь интерпретируем условия двойственной задачи. Если U_i – объективная цена за единицу ресурса, то левая часть неравенства двойственной модели представляет собой полные затраты на производство единицы продукции, а все неравенство отражает то, что произведенная стоимость C_i не может превышать суммарных затрат.

Значимость ресурса эквивалентна его дефицитности. Поэтому критерий двойственной задачи можно интерпретировать как суммарную дефицитность ресурсов, которую следует минимизировать.

Двойственный симплекс-метод

Отличие двойственного метода: в начальном и последующих базисных решениях выполняются условия оптимальности (все оценки неотрицательны при максимизации), но вектор Х неположителен, а значит, недопустим. В разрешимой задаче итерации метода приводят к допустимому Х, который и будет оптимальным решением задачи.

Цикл начинается с анализа базисных переменных. Если все переменные неотрицательны, вычисления завершаются. Иначе выбирается направляющая сторока k по минимальной базисной переменной. Вычисляются значения : для ά_kj < 0

Формула следует из требования соблюсти в новом решении условия оптимальности. При отсутствии в направляющей строке отрицательных _kj констатируется неразрешимость задачи из-за противоречивости условий.

Направляющий столбец r определяется по минимальному . Далее текущая симплекс-таблица пересчитывается так же, как в прямом методе. В результате получается новое базисное решение, в котором, по крайней мере, x_k станет неотрицательной. В разрешимой задаче такой алгоритм приведет к оптимальному решению за конечное число итераций.

П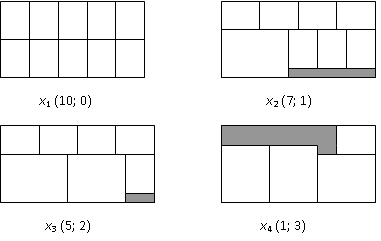 ример: Пусть заготовки вырезаются из прямоугольных листов размером 510. Необходимо наилучшим образом выполнить заказ, включающий два вида прямоугольных заготовок: 650 штук размером 22.5 и 1300 – размером 34. В качестве критерия возьмем расход материала (листов), а за переменные x_j примем количество листов, раскраиваемых j-м способом. Все возможные карты раскроя показаны на рис. Каждой карте соответствует своя переменная и количество получаемых заготовок (в скобках).

М одель задачи:

L=x₁+x₂+x₃+x₄  min

10x₁+7x₂+5x₃+x₄  650;

x₂+2x₃+3x₄  1300;

Таблица 0		0	1	1	1	1	0	0
Csi	Базис	A0	A1	A2	A3	A4	A5	A6
0	x5	-650	-10	-7	-5	-1	1	0
0	x6	-1300	0	-1	-2	-3	0	1
L, Δj		0	-1	-1	-1	-1	0	0
Zj		0	0	0	0	0	0	0
		--	--	1	1/2	1/3	--	--

x_j  0.

Канонический вид (умножен на –1):

-10x₁ - 7x₂ - 5x₃-x₄ +x₅ = - 650;

- x₂ - 2x₃ - 3x₄ + x₆ = -1300.

Как видно из таблицы, начальное базисное решение является недопустимым (отрицательным), но удовлетворяет условиям оптимальности (Δ_j  0). Поэтому последующие действия будут направлены на достижение доп. решения при сохранении условий оптимальности.

Таблица 1		0	1	1	1	1	0	0
Csi	Базис	A0	A1	A2	A3	A4	A5	A6
0	x5	-650/3	-10	-20/3	-13/3	0	1	-1/3
1	x4	1300/3	0	1/3	2/3	1	0	-1/3
L, Δj		1300/3	-1	-2/3	-1/3	0	0	-1/3
		--	1/10	1/10	1/13	--	--	1

В качестве направляющей берем строку с минимальной базисной переменной (x₆= -1300). Вычисляем значения , минимальное из которых определяет направляющий столбец. Тем самым определен и направляющий элемент. Выполнив симплекс-преобразование, получаем новое базисное решение.

Таблица 2		0	1	1	1	1	0	0
Csi	Базис	A0	A1	A2	A3	A4	A5	A6
1	x3	50	30/13	20/13	1	0	-3/13	1/13
1	x4	400	-20/13	-9/13	0	1	2/13	-5/13
L, Δj		450	-3/13	-2/13	0	0	-1/13	-4/13

Так как в этом решении есть отрицательная переменная, проводим следующую итерацию.

Здесь базисные переменные положительны, значит, решение допустимое. Условия оптимальности, как и в предыдущих решениях, выполняются. Таким образом, в табл. 2 имеем оптимальное решение задачи раскроя: