Прыёмы вучэбнай работы характэрызуюць спосабы здзяйснення вучэбнай дзейнасці. Яны падпарадкаваны вучэбным задачам, якія патрабуюць прымянення таго або іншага прыёма, ужо засвоенага вучнямі або новага.

Усеагульнымі ў матэматыцы як навуцы з’яўляюцца адносіны “больш”, “менш”, “роўна”. На аснове іх В.В.Давыдаў прапануе наступную паслядоўнасць вывучэння рацыянальных лікаў у падручніках па матэматыцы для пачатковых класаў.

1. Параўнанне канкрэтных велічынь ( даўжыні, плошчы, аб’ёму) спачатку “на вока”, а затым накладаннем, прыкладаннем, пераліваннем і г. д.

2. Мадэляванне велічынь адрэзкамі. Параўненне велічынь з дапамогай адрэзкаў. Напрыклад:

А Б В Параўнанне

Ё мкасці адрэзкаў як мадэлей вады А ёмкасцей вады

Б Б

3. Абазначэнне адрэзкаў літарамі, іх параўнанне шляхам мадэлявання адносін літарамі А>Б, Б<А.

4 Ураўніванне мадэлей – адрэзкаў двумя спосабамі з запісам выніку літарамі: А = Б + В – паяўленне дзеяння складання, А - Б = В – паяўленне дзеяння аднімання.

5.Увядзенне мерак па вымярэнню велічынь. Мадэляванне велічынь адрэзкамі. Вымярэнне адрэзкаў меркай і паяўленне паслядоўнасці цэлых неадмоўных лікаў.

. . . . . . . . . . . мерка

0 1 2 3 4 5

П аменшым мерку ў 2 разы: новая мерка

6. Пераход да меншай меркі і ўвядзенне дзеяння множання.

. . . . . . . . . . .

0 1 2 3 4 5 6 7 8 9 10 5•2=10

7. Пераход ад меншай да большай меркі і ўвядзенне дзеяння дзялення : 10 : 2 = 5.

8. З дапамогай мадэлявання і пераходу да мерак у 10 разоў большых (меншых) за дадзеную ўводзяцца таксама дзесятковыя дробы, працэнты і дзеянні над імі

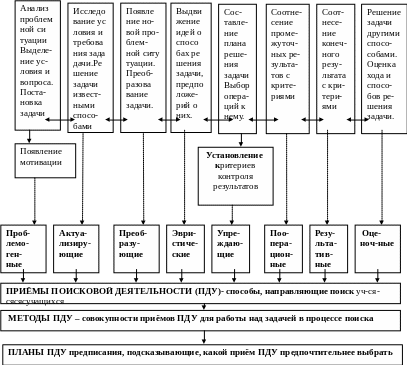
Основным недостатком методики постановки и реше-ния задач является неразработанность способов управле-ния их составлением и решением путём самостоятельной поисковой деятельности учащихся (приёмов, методов и планов ПДУ). Создание таких способов вытекает из на-шей модели, учитывающей узловые элементы теории функциональных систем академика П.К. Анохина.

(1) (2) (3) (4) (5) (6) (7) (8)

-

\\\\

1-ый момент начинается с осознания решающим проблемной ситуации математического содержания, с анализа этой проб-лемной ситуации, вычленения области поиска, установления известных и неизвестных данных задачи и формулировки её требования. Для преодоления затруднений в прохождении данного момента разработаны проблемогенные приёмы ПДУ, облегчающие анализ проблемной ситуации с целью выделения условия и вопроса и формулировки проблемы в виде задачи.

2-ой момент. Решающий обычно пытается исследовать условие и вопрос задачи. Ученик, как показывают наблюдения, всегда ищет ответ задачи на основе известных способов решения, привлекает известные математические знания и собственный опыт. С целью улучшения эффективности такой работы разработаны актуализирующие приёмы ПДУ ( припоминание знаний и др.)

3.-ий момент. В связи с тем, что ученик решает задачу проблемного характера на основе известных знаний и прошлого опыта, которых ему недостаточно, часто возникает новая проблемная ситуация. Тогда решающий перекодирует задачу (записывает её в других знаках, символах), переформулирует задачу (изменяет её словесное оформление), чтобы свести её к известной, аналогичной задаче, которую он уже решал. При этом ученик привносит новые математические сведения, изменяя форму представления данных и требований задачи. Чтобы поиск был результативным, используются преобразующие приёмы ПДУ (краткая запись задачи, её моделирование в виде рисунка,чертежа,таблицы,схемы).

4-ый момент. В результате предыдущей поисковой работы у учащихся может возникнуть предположение о способе реше-ния задачи. Они обычно пытаются обосновать его, предста-вить в виде гипотезы. Для облегчения этой работы служат эвристические приёмы ПДУ: решение простых задач, входящих в составную; решение части задачи; решение аналогичной сюжетной задачи; припоминание нужного правила и др.

5-ый момент. Возникшее и обоснованное предположение, в свою очередь, приводит к определённым действиям, осущес-твляемым в определённой последовательности, т.е. к плану решения задачи. К каждому пункту плана подбираются соответствующие операции. В это же время актуализируются из памяти приблизительные параметры будущих результатов, критерии их контроля и оценки Для предупреждения возмо-жных ошибок служат упреждающие приёмы ПДУ: прикидка результата и др.

6-ой момент. Выполняя операции, связанные с каждым пунктом плана, решающий соотносит их с прогнозируемыми параметрами и критериями. Если получение промежуточных результатов им соответствует, то деятельность решающего продолжается, в противном случае, прекращается. Тогда решающий обычно пытается вернуться на предыдущие этапы. Для повышения результативности такой работы на промежуточных этапах поиска решения и самого решения служат пооперационные приёмы ПДУ: установление границ операций и др.

7-ой момент. Конечный результат поисковой деятельности оформляется в виде ответа, который соотносится с выделяе-мыми критериями. К ним относятся известные способы проверки решения математических задач. В нашей модели они носят название результативных приёмов ПДУ. С помо-щью их оценивается весь процесс поиска решения задачи, констатируется возможность использования найденного способа для решения других задач.

.8-ой момент. Оценочные приёмы ПДУ помогают выбрать лучший из разных способов решения задач, который отличается краткостью, доступностью и простотой вычис-лений. Кроме того, эти приёмы приучают мысленно воспроизвести весь процесс поиска, ощутимые в нём трудности и подумать, как использовать их при поиске решения других задач (рефлексия). .

Рассмотренные приёмы ПДУ изучаются и применяются сначала разрозненно, а затем объединяются вместе при постановке и решении задач определённого класса, образуя своего рода совокупности приёмов ПДУ – методы поисковой деятельности учащихся. Для облегчения их актуализации и выбора приёма, адекватного классу задачи решаемой задачи, составлялются планы поисковой деятельности учащихся, обобщённость которых постепенно нарастает. Эти планы сначала даются в печатной, материализованной форме, затем проговариваются решающими вслух, позже про себя. Постепенно в процессе формирования у школьников учебно-поисковой деятельности приёмы, методы и планы ПДУ, эвристики, обобщаясь постепенно переходят во внутренний план. Обучение им и с помощью их целесообразно осущес-твлять по теории поэтапного формирования умственных действий П.Я. Гальперина.

Приведём пример карточки с задачей на поиск способа её решения.

Решите задачу по плану.

… . Выберите нужное, вставьте пропущенные числа и буквы в карточке по задаче: С трёх участков собрали 2 т 156 кг картофеля: с первого – 1000 кг, со второго – в 2 раза меньше. Сколько килограммов картофеля собрали с третьего участка?