Основные понятия математической статистики

План

1.Основные понятия математической статистики: 1.1.генеральная совокупность и выборка;

1.2.меры центральной тенденции: среднее арифме-тическое, мода, медиана;

1.3.статистическое и нормальное распределение;

1.4.меры разброса: размах,дисперсия и стандартное отклонение, коэффициенты вариации.

2.Расчёт мер центральной тенденции и разброса.

3.Составление репрезентативных выборок и эквивален-тных групп для исследования.

Ключевые компетенции: выборка и генеральная совокупность, среднее арифметическое, мода и медиана, размах, дисперсия, стандартног отклонение и вариация.

Литература

Качалко, В. Б. Методы психолого-педагогических исследований с применением математической статистики /В. Б.Качалко. –Мозырь: МГПУ им,И.П, Шамякина, 2008.—142 с. Глава 2.

1.ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ –это множество всех элементов, подлежащих исследованию.

Например, количество абитуриентов, поступающих в наш вуз. Из них выделяется часть поступивших в университет.

Выборка - это часть этой совокупности,

которую исследуют.

Из числа поступивших формируются ака-демические группы.

Репрезентативная выборка – это выборка, исследуя которую можно судить о свойствах всей генеральной совокупности.

Тесты для централизованного тестирования сначала проверяются на отобранной выборке так, чтобы она представляла все категории поступающих в вузы РБ.

Элементы выборки обозначают: х₁, х₂, …, х_n,

Их сумма х_i = х₁ + х₂ + … + х_n.

Количество каждого элемента выборки называют частотой. Обозначается f(x).

Если элементы выборки записать от наименьшего до наибольшего или наоборот, то выборку называют упорядоченной.

Для отбора для поступления выписывается набранное число баллов каждым абитуриентом, начиная с наибольшего или наименьшего..

Упорядоченную выборку с указанием частоты её элементов называют статистическим распределением.

К каждому полученному баллу ставится число абитуриентов его получившим (частота). Выясняется картина для отбора.

Сумму элементов выборки, делённую на количество элементов (объём выборки), называют средним арифметическим. Обозначают .

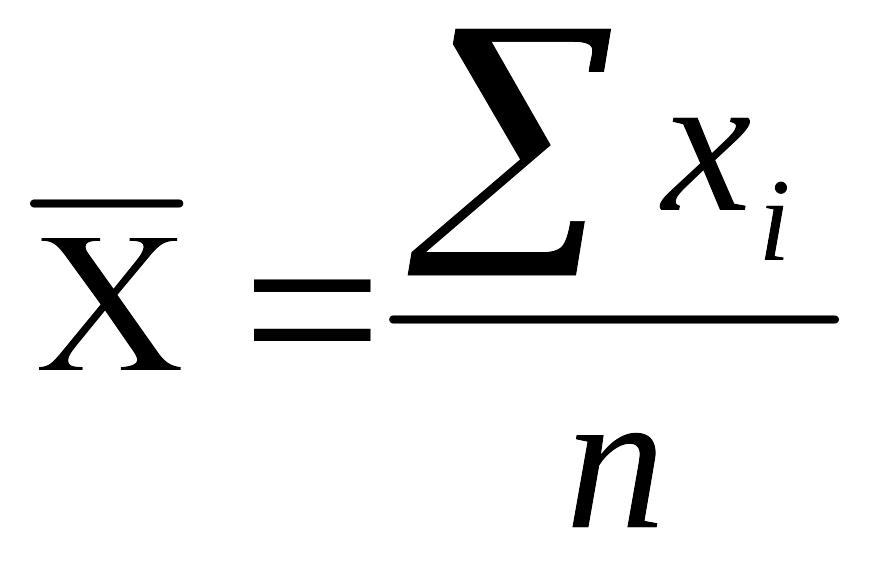Наиболее часто встречающийся элемент выборки называют модой. Обозначают Мо.

Элемент выборки, который стоит в середине статистического распределения, называют медианой. Обозначают Ме.

Разность между наибольшим и наименьшим элементом выборки называют размахом. Обозначают R.

Пример. Пусть баллы, полученные за тест: 5, 4, 4, 3, 3, 3, 3, 2, 2, 1. Тогда их статистическим распределением будет : «5» , «4», «3», «2» «1»

Частота : 1 2 4 2 1

Тогда модой и медианой будут: Мо=3, Ме=3.

С реднее арифметическое вычисляется делением на объём выборки суммы произведений величины каждого балла на его количество: Х= =

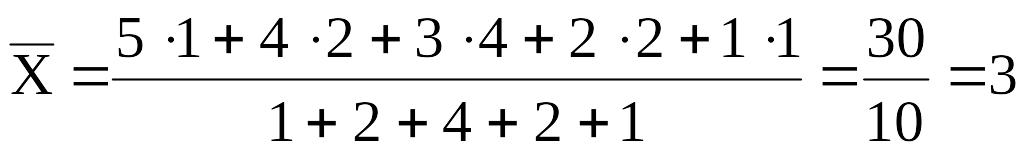
Е сли параметры Х, Мо и Ме равны или приблизительно равны, то статистическое распределение называют нормальным.

Рассмотрим теперь рассчёт по таблице мер ЦЕНТРАЛЬНОЙ ТЕНДЕНЦИИ (среднего арифметическогою моды и медианы) и РАЗБРОСА (размаха, дисперсии и стандартного отклонения, коэффициента вариации).

ТАБЛИЦА ДЛЯ РАСЧЁТА КРИТЕРИЕВ F и t, КОРРЕЛЯЦИИ r

Контрольн гр.	Эксп ер. гр.	Линейное отклонение		Квадратичное отклонение		Сопряжён-ность
		-	-	( )2	( - )2	( - )( - )
7	7	+3	+2	9	4	+6
6	7	+2	+2	4	4	+4
5	6	+1	+1	1	1	+1
4	6	0	+1	0	1	0
4	5	0	0	0	0	0
4	5	0	0	0	0	0
4	5	0	0	0	0	0
3	4	- 1	-1	1	1	+1
2	3	- 2	-2	4	4	+4
1	2	- 3	-3	9	9	+9
40	50	0	0	Σ= 28	Σ=24	Σ= 25

К онтрольные классы Эксперим. классы

Средние арифметические

Х=40:10= 4 У = 50:10 = 5

Дисперсии:

=28:(10-1)≈3,1 =24:(10-1)≈ 2,7

Стандартные отклонения . отклонения: = ≈1,76; = ≈ 1,64

Коэффициенты вариации

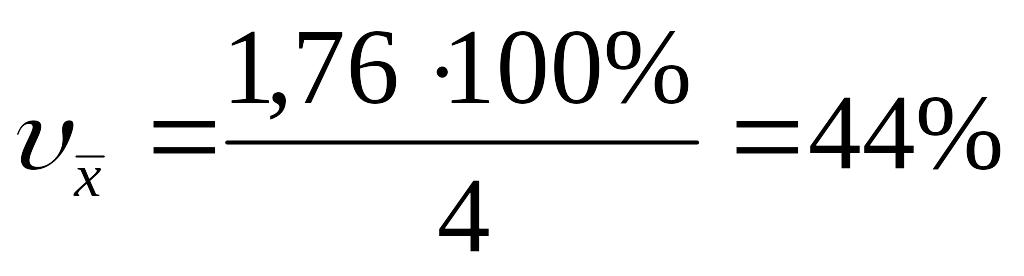
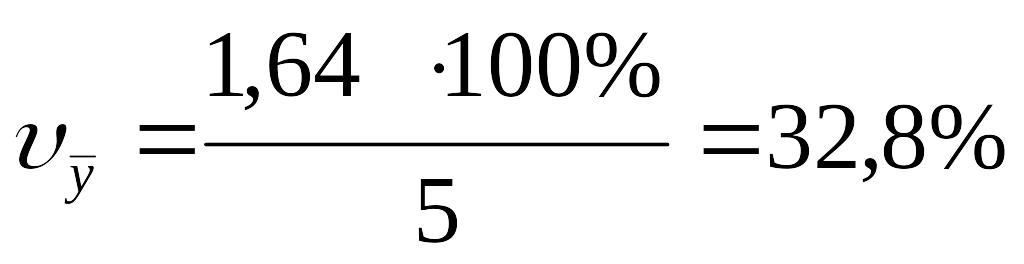
ФОРМУЛЫ мер разброса

Размах – разность между наибольшим (mах) и наименьшим (min) значением статистического распределения.

Дисперсия (σ²) - среднее квадратическое отклонение от среднего арифметического.

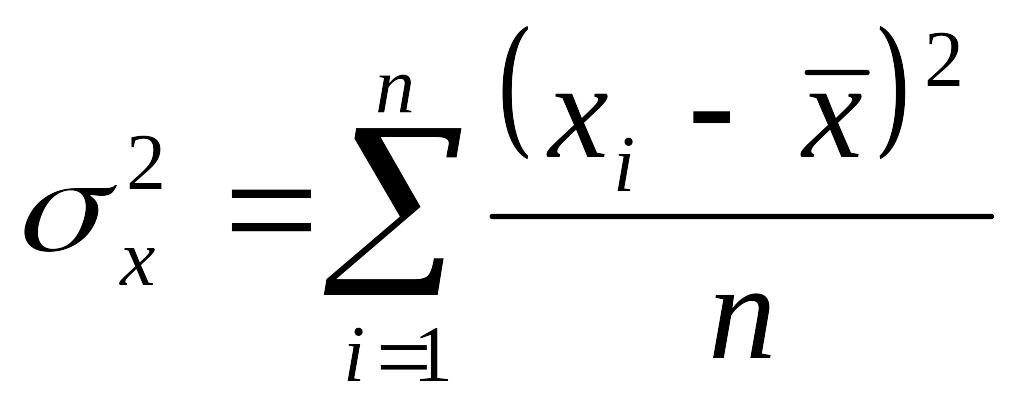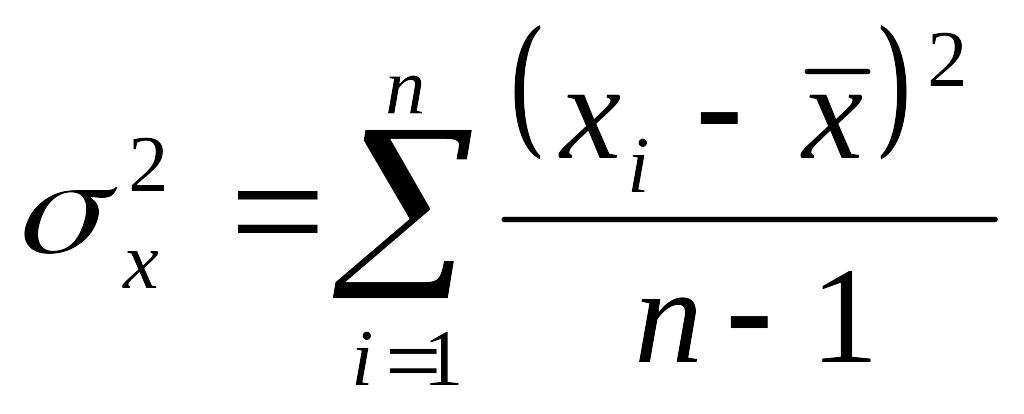, - дисперсии генеральной совокупности и выборки (n 30)

Стандартные отклонения от среднего арифметического генеральной совокупности 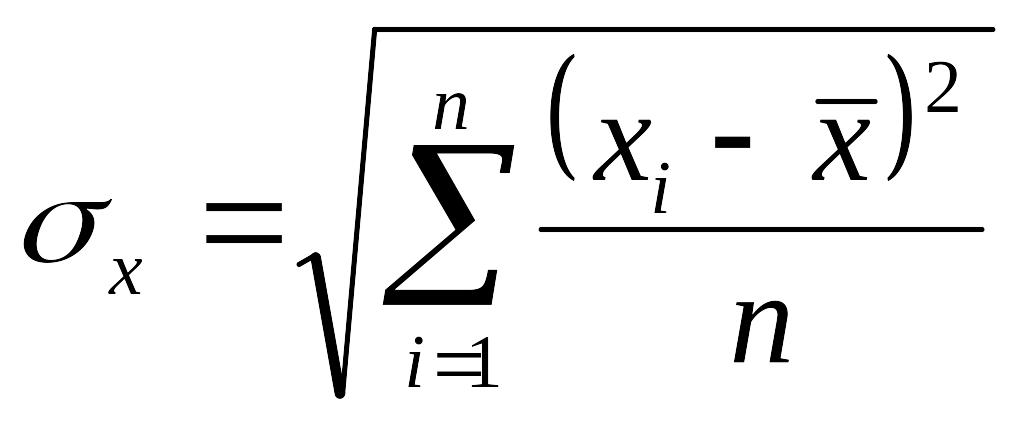и выборки для 30-и и менее испытуемых .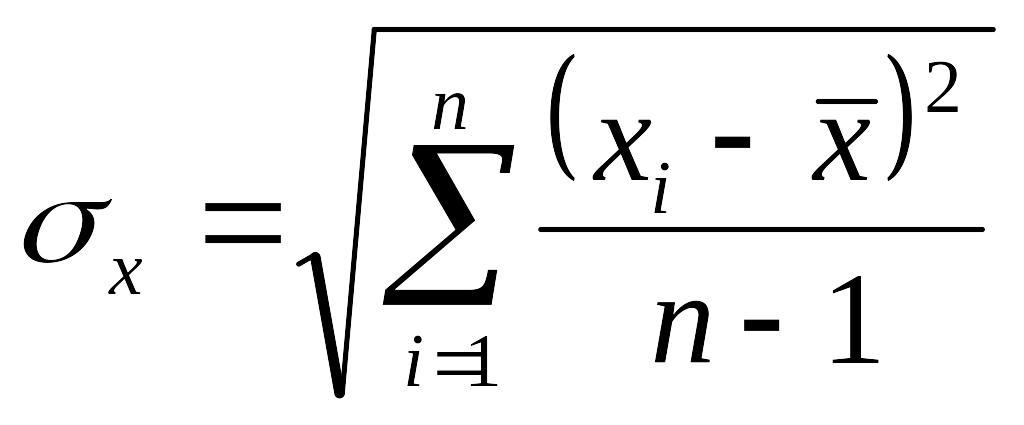

Коэффициенты вариации 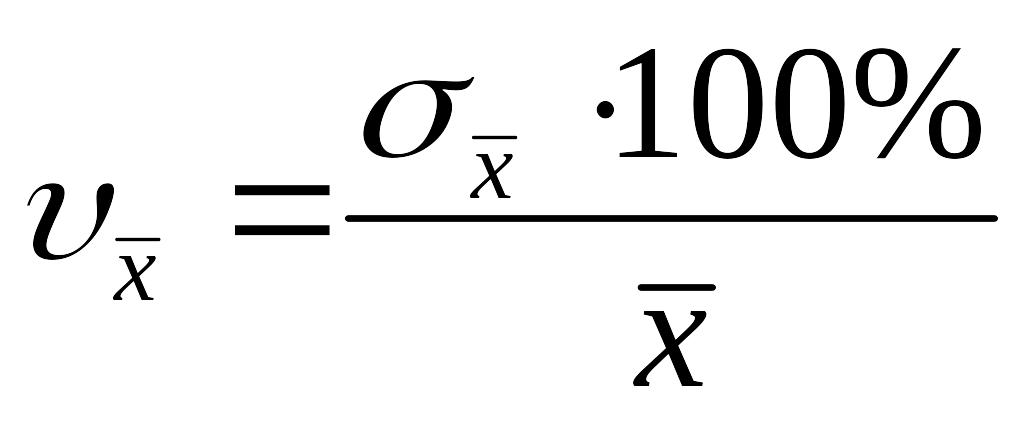; 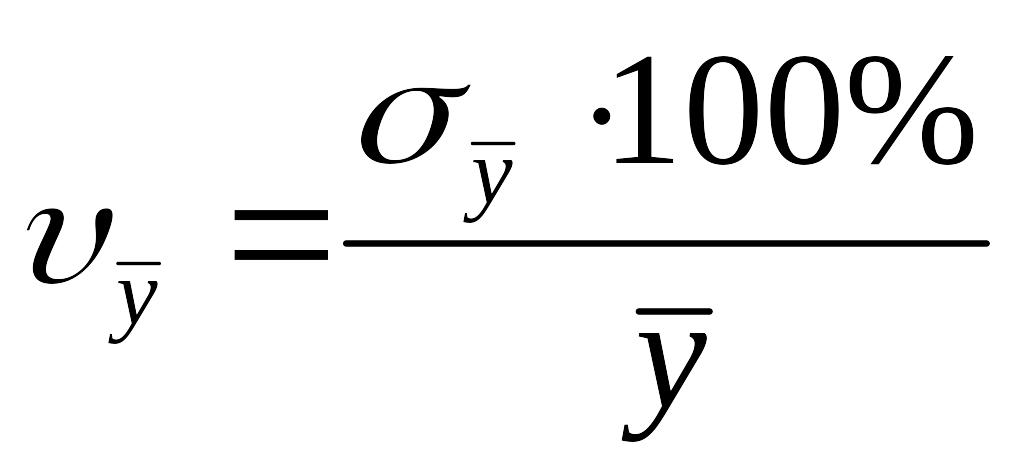для контрольной и экспериментальной групп.

Стандартные ошибки среднего арифметического _;

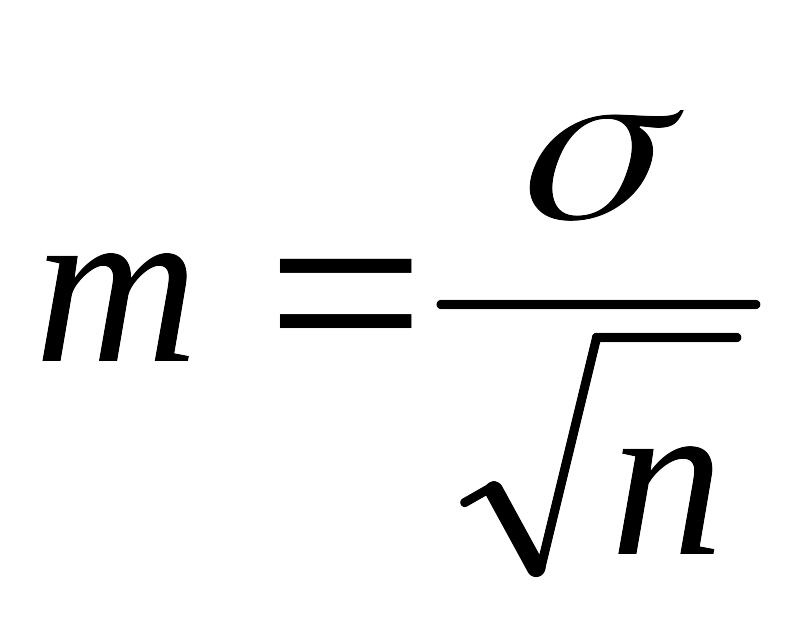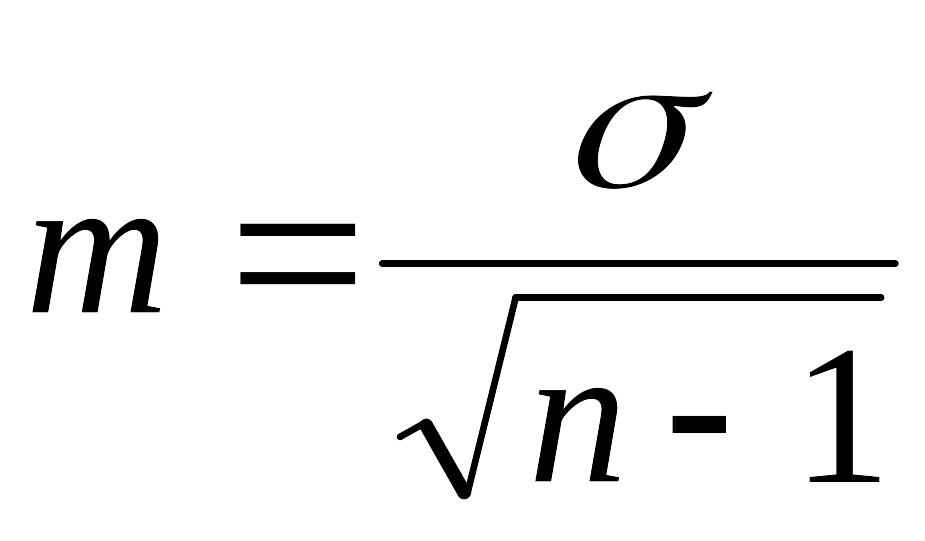
5. ВЫБОРОЧНЫЙ МЕТОД

По способу организации различают следующие виды выборочного метода:

1) случайный отбор, ориентированный на выборку элементов из генеральной совокупности при равной возможности каждому элементу попасть в выборку путём жеребьёвки либо с помощью таблицы случайных чисел;

2)механический отбор, при осуществ-лении которого совокупность делят на столько групп, сколько единиц должно войти в выборку, из них делают случайный выбор;

3) типический отбор, при котором генеральную совокупность делят на типические группы и из них делают выбор. Например, отдельно отбирают для исследования учеников городских и сельских школ.

СПОСОБЫ СОЗДАНИЯ ЭКВИВАЛЕНТНЫХ ГРУПП ДЛЯ СРАВНИТЕЛЬНОГО ЭКСПЕРИМЕНТА

1. Отбор в группы на основе предвари-тельного тестирования.

2. Попарный отбор в группы по итоговой успеваемости , по тесту или проверочной работе по исследуе-мому фактору.

Школы и классы выбирают на основе рандомизации (случайного выбора).

План

5. Структура эксперимента с применением математической статистики.

6. Статистические гипотезы и способы их проверки.

7. Критерии Фридмана и Стьюдента.

Ключевые компетенции: структура эксперимента, .

Литература

Качалко, В. Б. Методы психолого-педагогических исследований с применением математической статистики /В. Б.Качалко. –Мозырь: МГПУ им,И.П, Шамякина, 2008.—142 с. Глава 3.

1.СТРУКТУРАСРАВНИТЕЛЬНОГОЭКСПЕРИМЕНТА

При проведении исследований основнвм методом является сравнительный эсперимент, который про-водится по следующей схеме на эквивалентных экспеимертальной и контрольной группах.

Выбор, уравнивание классов	Экспе-римен-таль-ные клас-сы	Учебная работа с введением новоо фактора	Учеб-ная работа без нового фак-тора	Кон-трольные клас-сы
Определение начального уровня ЗУНов уч-ся по исследуе-мым вопросам	Нэ			Нк
Эксперимент
Определение ЗУНов в конце эксп.	Кэ			Кк
Прирост знаний.	Кэ-Нэ =Пэ		Кк-НкПк
6.Эффектив-ность эксп.
		П  Пэ-Пк

При сравнительном эксперименте необходимо:

1. Уравнять условия учебной работы, кроме экспериментального фактора, в экспериментальных и контрольных классах (группах).

2.Определить путём тестирования начальный уровень знаний, умений и навыков, развития учащихся экс- периментальных и контрольных классов (Нэ и Нк).

3.Провести учебную работу в экспериментальных классах с введением экспериментального фактора, а в контрольных классах без него.

4.Снова определить уровень знаний, умений и навыков, развития после эксперимента(Кэ,Кк).

5. В обоих случаях вычесть из средних показателей окончательных знаний средний показатель начальных знаний, умений и навыков учащихся экспериментальных и контролных групп (Кэ-НэПэ, Кк-НкПк).

6.Разности покажут прирост знаний, умений и навыков и развития в экспериментальных и контрольных классах

7.Вычислить сравнительную эффективность экспери-ментального фактора (Пэ-Пк) с применением анализа статистическими методами, который покажет эффек-тивность влияния нового фактора на учебный процесс .

Этот вид эксперимента является наиболее пригод-ным для исследований в общеобразовательной школе.

2.Статистическая гипотеза-это предположение, которое необходимо доказать с помощью критериев статитических с установленной достоверностью не менее 95% для психолого-педагогических исследований, с уровнем значимости 5%, или в десятичных дробях с достовенрн. 0,95 и уровнем значимости 0,05.

Уровень значимости – это вероятность отклонения нулевой гипотезы о том, что распределения не различаются, При отклонении нулевой гипотезы принимается альтернативная гипотеза, что распределения отличаются. Статистическую гипотезу в отличие от научной никогда не можно полностью доказать, но всегда можно отклонить. Ошибка отклонения верной статистической гипотезы не должна превышать 5%. Она называется уровнем значимости, который обозначается р 5% или р 0,05. Достоверность принятия верной статистической гипотезы тогда будет не менее 95% или 0,95.

В статистике вводится понятие степени свободы, которое всегда меньше на 1 числа опытов. Потому для каждой из выборок с количеством элементов п₁ и п₂ число степеней свободы будет соответствовать п₁ - 1 и п₂ - 1, а вместе (п₁-1)+(п₂-1)=п₁+п₂-2.

Для проверки статистических гипотез учёными составлены таблицы критических значений для каждого статистического критерия с учётом степеней свободы и уровня значимости : р=5% (достоверность 95%), р=1% (достоверность 99%) .

Общий порядок проверки статистических гипотез:

6. формулируется основная (проверяемая) и альтернативная гипотезы;

7. выбирается статистический критерий для проверки справедливости гипотезы;

8. определяется уровень значимости (достоверности) принятия гипотезы , а затем табличное значение критерия;

9. проводится исследование, по результатам которого расчитывается фактическое значение критерия;

10. на основе сравнения фактического и критического знач. делается вывод о правдоподобности или необходимости отклонения выдвинутой гипотезы.

Для принятия гипотезы требуется, чтобы вычисленное значение было не меньше табличного. Исключения бывают в некоторых непараметрических критериях (Вилкоксона, Манна- Уитни и др). Таблицы критических значений, правила их использования разрабатываются для каждого критерия.

Для проверки статистических гипотез при-меняются критерии Фишера (F) и Стьюдента (t).

Если вычисленное по формуле кри-терия значение равно или больше таблич-ного, то утверждают, что гипотеза под-

Вилась с достоверностью не ниже 95% .

Критерий Фишера определятся по формуле:

или наоборот, чтобы большая дисперсия делится на меньшую, поэтому всегда F 1.

Критическое значение критерия F находится по таблице для п₁–1 и п₂–1 степеней свободы, где п₁ и п₂ количество испытуемых в контрольной и экспериментальной группах. Для нашего случая F=3,1:2,7=1,15 при п₁-1=10-1=9 и п₂–1=10-1=9 степенях свободы. На пересечении указанных строк и столбцов находим по таблице критических значений критерия F для достоверности 95% значение 3,18. Так как 1,15 меньше 3,18, принимается ну-левая гипотеза, различие несуществен-ное между распределениями,то экспе- иментальная гипотеза отклоняется.

Критерий Стьюдента t вычисляется по

формуле:

, где и , и - соответствующие параметры кон-трольной и экспериментальной групп, а п₁ и п₂ – количество испытуемых в этих группах.

Для нашего случая имеем

Далее находим критическое значение по таблице критерия t для достоверности 95% и п₁ + п₂ – 2 = 10 + 10–2 =18 степеней свободы. Оно равно 2,1. Так как 1,32 меньше 2,1, принимается нулевая гипотеза меньше 2,1, различие между выборками несущественное то экспериментальная гипотеза не подтвердилась.

Для повторных измерений на одной и той же выборке испытуемых применяется другая формула критерия Стьюдента:

, где

d – разность между данными каждой пары;

d – сумма разностей с учетом знаков;

(d)² – квадрат суммы разностей; n – число пар испытуемых.

Эта формула применяется в основном на одних и тех же испытуемыхю

Результат исследования проверяется по таблицам критических значений для п-1 = степеней свободы для установления достоверности различия не меньше 95%, или не больше 5% уровня значимости.

ПРИМЕНЕНИЕМ ПРИБЛИЖЁННЫХ ВЫЧИСЛЕНИЙ

При проведении научных исследований приходится измерять разный материал, получая при этом числовые данные с заданной точностью. 1.Чтобы округлить число с точностью до указанного разряда, нужно цифры, стоящие правее этого разряда, отбросить в дробной части числа или заменить нулями в целой части числа Последняя сохраняемая цифра округляется по правилам округления:

2.1.Если первая отбрасываемая цифра больше пяти, то в последнем сохраняемом разряде цифра увеличивается на единицу: 2126 ≈ 2 130 (до десятков)

2.2.Если первая отбрасываемая цифра пять и за ней есть ещё цифры, отличные от нуля то в последнем сохраняемом разряде цифра увеличивается на единицу.

2.3.Если первая отбрасываемая цифра пять и за ней больше никаких цифр за исключением нулей, то пос-леднюю сохраняемую цифру оставляют без изменения, если она чётная; увеличивают на единицу, если она нечётная.: 21, 265007 ≈21,26; 21, 275008 ≈21,28.

3.При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных зна-ков, сколько их в приближённом числе с наименьшим числом десятичных знаков.

4. При умножении и делении приближённых чисел в результате следует сохранять столько значащих цифр, сколько их имеет наименее точное из данных чисел.

5. При вычислении промежуточных результатов следует сохранить одну лишнюю запасную цифру, которую в окончательном результате надо отбросить.

ПОНЯТИЕ О КОРРЕЛЯЦИИ, РЕГРЕССИИ

И НОРМАЛЬНОМ РАСПРЕДЕЛЕНИИ

План

1.Линейная корреляция.

2. Линейная регрессия.

3. Нормальное распределение.

Литература: Качалко, В. Б. Методы психолого-педагогических исследований с применением математической статистики /В. Б. Качалко.—Мозырь: УО МГПУ им. И.П. Шамякина.

—2006.---107 с. – Гл. 4.

Корреляция – это статистическая взаимо-связь между переменными, которая при этом не носит причинно-следственного характера как в эксперимен0-те.

Коэффициент линейной корреля-ции – показатель направления и степени взаимосвязи. Изменяется от +1 (полная положительная корреляция) через 0 (отсутствие корреляции) до –1 (полная отрицательная корреляция).

При r = 1 и r = -1 имеем линейную функциональную зависимость (прямую и обратную) .

Коэффициент линейной корреляции Пирсона вычисляется по формуле:

. Имеем

для рассматриваемого случая, где N=10 – количество сравниваемых пар.

Далее проверяем результат по таблице критичес-ких значений коэффициента Пирсона для п-2 =10-2=8 степеней свободы. Находим r = 0,63. Так как 0,87 больше 0,63, то корреляция существенная между двумя выборками с достоверностью 95%.

Регрессия - зависимость среднего значе-ния величины У от величины Х ( ) или значения Х от величины У ( ). Эта зависи-мость обычно определяется уравнениями линейной регрессии. Это позволяет прогно-зировать психолого-педагогические явления. Уравнения регрессии и коэффициенты к ним вычисляются по формулам с учётом рассматриваемого примера:

_{, ,}

_,

_,

Построим графики уравнений по точкам: А(0;-0,16), В(0,15;0), С(0;0,51), D(-0,45;0).

+1

+0,51 С

-0,45 D

В

-1

-0,16 А

0,15

+1

+2

Существуют ещё и другие формулы коэффициен-тов корреляции, требующие меньшего числа расчётов.Этот клэффициент часто используется при исследовании существоаания связи между разныими явлениями: курением и заболеваемос-тью гриппом, алкоголем и спортивными успехами,

питанием трансгенными продуктами и здоровьем.

Таким образом, коэффициент линейной корре-ляции позволяет не только выявить направление, но и величину связи между явлениями, однако он не указывает на причину этой связи как экспери-мент.На практике применяется другая формула r. _,

где х_і и у_і полученные п учащимися баллы.

где х_і и у_і полученные п учащимися баллы.

х _і у_і х_i² у_i² х_і•у_і Существует ли связь

2 1 4 1 2 между уровнем знаний 3 2 9 4 6 по чтению х_і и письму у_і

3 4 9 16 12 у 10 младшишкольников?

4 4 16 16 16 10•346-56•51

5 4 25 16 20 r =

6 5 36 25 30 10•374-56² • 10•327-51²

7 6 49 36 42 3460- 2856

8 7 64 49 56 3 740-3 136• 3 270-2601

9 8 81 64 72 ≈ 0,95.

9 10 81 100 90

5 651374 327 346

Проверяем r по таблице критических значений для п-2 =10-2=8 для 95% и 99%. Имеем 0,63 и 0,77. Так как 0,95 >0,77, существует высокая корреляция между уровнем знаний по чтению и письму с достоверностью 99%.

Нормальное распределение в системе координат изображается колоколоподобной кривой Гаусса,

где σ – стандартное отклонение

-3σ -2σ -1σ Х=Ме=Мо +1σ +2σ +3σ

6 8, 3%

95,5%

99%

Асимметрия равна 3(Х– Ме) : σ_x. Если:

а симметрия равна нулю, то распределение нормальное, а также: Х = Ме = Мо, где Х или m—ср.арифм., Ме—медиана, Мо-мода.

Е сли: 2) Х< Ме < Мо - то отрицательная асимметрия;

3) Х> Ме > Мо - то положительная асимметрия.

Критерии распознавания нормальных распределений:

1 .Среднее арифметическоеХ или m, мода (Мо) и

медиана (Ме) распределения равны или

приблизительно равны.