МОДЕЛЬ ПОСТАНОВКИ И РЕШЕНИЯ УЧЕБНОЙ ЗАДАЧИ

Основным недостатком методики обучения решению задач является объяснение способов решения типовых задач с последующим их закреплением, неразра-ботанность способов упра- вления их составлением и решением путём самостоя-тельной поисковой деятельности учащихся (ПДУ) (приёмов, мето-дов,планов ПДУ и эвристик)). Создание таких способов выте-кает из приведенной модели, учитывающей современные нейропсихологические исследо-вания, прежде всего мозга

1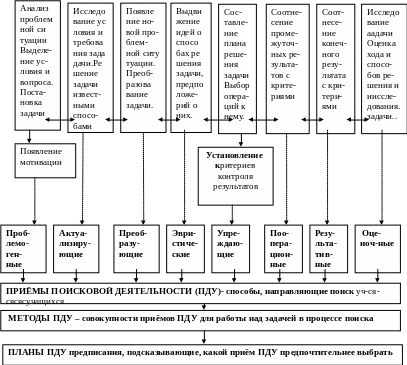 2 3 4 5

6 7 8

(1) (2) (3) (4) (5) (6) (7) (8)

От хорошего функционирования мозга во многом зависит успех в деятельности человека, а у обучаемого его учебно-поиско-вой деятельности (ПДУ). Она-то как раз и осу-ществляется им при поиске решения учебных задач, системы которых должны быть созда-ны в каждом учебном предмете. Была разработана модель учебной задачи на основе теории функциональных систем академика П.К. Анохина. Модель предложена для ксерокопирования. Предлагаем описание 8 моментов постановки и решения задачи. К каждому моменту разработаны некоторые приёмы поисковой деятельности учащихся (ПДУ). Они носят эвристический характер и призваны облегчить прохождение каждого из 8 моментов работы мозга в нашей модели. Появление недорогих ЭВМ с большим объёмом оперативной памяти, а также средств для оперативного выявления затруд-нений при поиске решения задач позволяет этот процесс сделать самоупра-вляемым. 1-ый момент. Постановка любой задачи начинается с выделение её структурных элементов путём анализа проблемной ситуации, вычленения области поиска, установления известных и неизвестных данных задачи и формулировки её требования. Для преодоления затруднений в прохождении данного момента разработаны проблемогенные приёмы ПДУ, облегчающие анализ проблемной ситуации с целью выделения условия и вопроса и формулировки проблемы в виде задачи.

2-ой момент. Решающий обычно пытается исследовать условие и вопрос задачи. Ученик, как показывают наблюдения, всегда ищет ответ задачи на основе известных способов решения, привлекает известные математичес-кие знания и собственный опыт. С целью улучшения эффективности такой работы разработаны актуализирующие приёмы ПДУ ( припоминание теоретических знаний и др.)

3-ий момент. В связи с тем, что ученик решает задачу проблемного характера на основе известных знаний и прошлого опыта, которых ему недостаточно, часто возникает новая проблемная ситуация. Тогда решаю-щий перекодирует задачу: записывает её в других знаках, символах, переформулирует задачу (изменяет её словесное оформление), чтобы свести её к известной, аналогичной задаче, которую он уже решал. При этом ученик привносит новые математические сведения, изменяя форму представления данных и требований задачи. Чтобы поиск был результа-тивным, используются преобразующие приёмы ПДУ (краткая запись задачи, её моделирование в вид рисун-ка,чертежа,таблицы,схемы).

4-ый момент. В результате предыдущей поисковой работы у учащихся может возникнуть предположение о способе решения задачи. Они обычно пытаются обосновать его, представить в виде гипотезы. Для облегчения этой работы служат эвристические приёмы ПДУ: решение простых задач, входящих в составную; решение части задачи; решение аналогичной сюжетной задачи; припоми-нание нужного правила и др.

5-ый момент. Возникшее и обоснованное предположение, в свою очередь, приводит к определённым действиям, осуществляемым в определённой последовательности, т.е. к плану решения задачи. К каждому пункту плана подбираются соответствующие операции. В это же время актуализируются из памяти приблизительные параметры будущих результатов, критерии их контроля и оценки Для предупреж-дения возможных ошибок служат упреждающие приёмы ПДУ: прикидка результата и др.

6-ой момент. Выполняя операции, связанные с каждым пунктом плана, решающий соотносит их с прогнозируемыми параметрами и критериями. Если получение промежуточных результатов им соответ-ствует, то деятельность решающего продо-лжается, в противном случае, прекращается. Тогда решающий обычно пытается вернуться на предыдущие этапы. Для повышения результативности такой работы на промежу-точных этапах поиска решения и самого решения служат пооперационные приёмы ПДУ: установление границ операций и др.

7-ой момент. Конечный результат поисковой деятельности оформляется в виде ответа, который соотносится с выделяемыми кри-териями. К ним относятся известные способы проверки решения математических задач. В нашей модели они носят название результативных приёмов ПДУ

8-ой момент. Оценочные приёмы ПДУ помогают выбрать лучший из разных способов решения задач, который отличается краткостью, доступностью и простотой вычислений. Кроме того, эти приёмы приучают мысленно воспроизвести весь процесс поиска, ощутимые в нём трудности и подумать, как использовать их при поиске решения других задач (рефлексия).

Кроме того после решения рекомендуется щё провести дополнтельную работу нал задачей исследовательского характера: выбрать из несколь-ко возможныз наиболее рациональный способ решения залачи: изменить вопрос, условие задачи (числовые данные, отношения, величины задачи и др.) и пронаблюдать, как это повлияет на ответ задачи, можно ди сделать какие-либо выводы.

Рассмотренные приёмы ПДУ изучаются и применяются сначала разрозненно, а затем объединяют-ся вместе при постановке и решении задач определённого класса, обра-зуя своего рода совокупности приёмов ПДУ – методы поисковой деятельности учащихся. Для облегчения их актуализации и выбора приёма, адекватного классу задачи решаемой задачи, составлялются планы поисковой деятельности учащихся, обобщённость которых постепенно нарастает. Эти планы сначала даются в печатной, материа-лизованной форме, затем проговариваются решающими вслух, позже про себя. Постепенно в процессе формиро-вания у школьников учебно-поисковой деятельности приёмы , методы и планы ПДУ, эвристики, обобщаясь постепенно переходят во внутрен-ний план. Обучение им и с помощью их целе-сообразно осуществлять по теории по-этап-ного формирования умственных действий.

СОСТАВЛЕНИЕ КАРТОЧЕК ДЛЯ САМОСТОЯТЕЛЬНОГО ПОИСКА РЕШЕНИЯ ЗАДАЧИ

Приведём пример карточки с задачей на поиск способа её решения.

Решите задачу по плану.

Выберите нужное, вставьте пропущенные числа и буквы в карточке по задаче: С трёх участков собрали 2 т 156 кг картофеля: с первого – 1000 кг, со второго – в 2 раза меньше. Сколько килограммов картофеля собрали с третьего участка?

1 . Прочитайте задачу 1-ый уч. ---- кг

сделайте её краткую 2-ой уч.в -- раза меньше 2 156 кг

запись 3-ий уч. ? кг

2.Составьте выражение 1) 2 156 – 1 000 : 2

и проверьте его по 2) 2 156 : 2 – 1 000

перфокарте 3) 2 156 – (1 000 :2 + 1 000)

4) 2 156 – 1 000 – 1 000 : 2

5) 2 156 – 1 000 : 2 – 1 000

3. Запишите решение задачи …………………

4. Запишите ответ………………………………………

5.Проверьте: ----- + -- (кг) картофеля собрали с 1 и 2 участков,

решение в ---- раза масса картофеля со 2 участка меньше

массы картофеля с 1 участка.

6. Исследуйте задачу. Как будет изменяться масса картофеля, собранного с третьего участка, если масса картофеля, собранного со 2-го участка, будет меньше массы картофеля, собранного с первого участка, в 4 раза? в 5 раз?

7. Ответ проверьте по перфокарте:

1. увеличится в несколько раз;

2. увеличится на несколько единиц;

3. уменьшится в несколько раз;

4. уменьшится на несколько единиц

Перфокарта

Задания	Ответы
1	П 1	П 2
2	П 1	Прав.
3	Прав.	П 2
4	Прав.	П 2

П1.Решите похожую задачу: С трёх участков собрали

2 000 кг картофеля: с первого – 1 000 кг, а со

второго – 500 кг. Сколько килограммов картофеля собрали с третьего участка?

П 2. Сделайте к этой задаче чертёж:

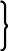1 уч. |------------| ….кг

2 уч. |-----| в ---- раза меньше … ___кг

3. уч. |--------|….кг.

Перфокарта заклеивается плотной бумагой с наколками, сделанными на швейной машине, как на почто-вых марках по форме клеточек. Клеточка открывается шари-ковой ручкой. Если ответ правильный, то в клетке стоит «Прав.». Если ответ неправильный, указывается помощник (П1,П2), записанный справа. В дальнейшем перфокарты в обучении поиску решения задач можно заменить персо-наль-ным компьютером с программой, содержащей банк посте-пенно усложняющихся задач и индивидуальной мерой помо-щи, исходя из уровня подготовки к поиску каждого решаю-щего (зоны его ближайшего развития), в виде подсказок, приёмов, методов и планов ПДУ.

В текст карточек для самостоятельной работы полезно включать планы по использованию: методов и приёмов ПДУ; эвристических подсказок (по оформлению решения, его проверке, по выбору рационального способа решения оценке решения, по дополнительной работе над задачей) Для осуществления мониторинга за процессом составле-ния задачи и поиска решения, проверки и оценки решения создаются тесты (входные, формирующие, диагностические, итоговые).

Применение указанных рекомендаций позволяет осуществлять эффективный поиск способа решения задач даже учащихся со слабой теоретической подготовкой и невысоким уровнем развития поисковой деятельности. Ещё более значительно можно повысить продуктивность самостоятельного поиска решения задач приме-нение заложенных в память ПЭВМ батарей задач с нарастающей трудностью решения с приёмами, методами, планами ПДУ, эвристическими подсказками, предложенными с учётом выявлено тестированием зоны ближайшего раз-вития обучаемого.

ПАЧАТКОВАЕ НАВУЧАННЕ РАШЭННЮ САСТАЎНЫХ

НА АСНОВЕ ПРОСТЫХ ЗАДАЧ. Спосабы разбору задачы

План

1. Класіфікацыя простых задач.

2.Азнаямленне з простай і састаўной задачай.

3. Агульныя спосабы разбору задачы.

Літаратура

Асноўная: 1, гл.3 п.20 2, гл. 4. пп.4.3-4.4 Дадатковая: 3, гл.3, п.п. 4-5.

В.Б. Качалко. Метады актыўнага навучання матэматыцы ў пачатковых класах / В. Б. Качалко.—Мінск: МГПУ ім. М. Горкага, 1984. – 79 с.

Ключавыя словы: практычная і вучэбная задача, састаўныя задачы, разбор задачы, прыёмы і планы разбору.

КЛАСІФІКАЦЫЯ ПРОСТЫХ ЗАДАЧ.

Найбольш вядомая класіфікацыя простых задач:

1-ая група (5 відаў) - на знаходжанне:

1) сумы; 2) астатка; 3) сумы аднолькавых складаемых (здабытку); 4) дзяленне на роўныя часткі Пр.: Паклалі 8 груш пароўну на дзве талеркі. Колькі груш на кожнай талерцы? ; 5) дзяленне па зместу Пр.: Расклалі на талеркі 6 груш па 2 на кожную. Колькі талерак спатрэбілася?

2-ая група (8 відаў) - на сувязь паміж кампанентамі і вынікамі арыфметычных дзеянняў. Пр.: а) Купілі 3 сшыткі ў клетку і 5 – у лінейку. Колькі ўсяго купілі сшыткаў? б) Усяго купілі 8 сшыткаў у клетку і лінейку, з іх 3 сшыткі ў клетку. Колькі сшыткаў купілі ў лінейку? і інш..

3 - яя група (8 відаў) – на павялічэнне (памян-шэнне) ліку на некалькі адзінак і ў некалькі разоў ва ўскоснай і прамой форме. Пр.: а) Было 9 алоўкаў, што ў 3 разы больш, чым маркераў. Колькі было маркераў? (ускосная форма)

б) Было 9 алоўкаў, а маркераў- у 3 разы менш. Колькі было маркераў? (прамая форма).

4-я група (4 віды) – на параўнанне: рознаснае

( на колькі больш-менш) і на кратнае ( у колькі разоў больш-менш).

5-ая група (2 віды) -- на знаходжанне долі ад ліку і ліку па яго долі.

Пр.: а) Кілаграм цукерак каштуе 6 тысяч рублёў. Колькі каштуе 1/3 кг цукерак?

б) 1/3 кг цукерак каштуе 2 тысячы рублёў. Колькі каштуе 1 кг цукерак? або: Якая цана цукерак?

У пачатковым курсе матэматыкі задачы рашаюцца для:

1. засваення тэарэтычнага матэрыялу (плошча квадрата);

2. засваення прыёмаў арыфметычных вылічэнняў;

3. развіцця лагічнага мыслення (аналіз, аналогія і інш.); 4) кантролю ведаў, уменняў і навыкаў;

5. дыягностыкі разумовага развіцця вучняў.

АЗНАЯМЛЕННЕ МАЛОДШЫХ ШКОЛЬНІКАЎ З ПРОСТАЙ І САСТАЎНОЙ ЗАДАЧАМІ

У класе праводзіцца гульня “Магазін”, ствараецца задачная сітуацыя,з якой выдзяляецца тэкставая задача:

Маша купіла 5 бананаў і 4 грушы. УМОВА ЗАДАЧЫ

Колькі ўсяго фруктаў купіла Маша? ПЫТАННЕ ДА ЯЕ

5 І 4 лікавыя дадзеныя задачы

Колькасць купленых фруктаў ШУКАЕМАЕ ЗАДАЧЫ

5 + 4 = 9 (фр.) РАШЭННЕ ЗАДАЧЫ

Маша купіла 9 фруктаў. АДКАЗ ЗАДАЧЫ

1-ы варыянт

У далейшым задачу можна перафармуляваць у другую з двума пытаннямі, а пазней пакінуць апошняе пытанне:

Маша купіла 5 бананаў, а груш- на 1 менш.

Колькі груш купіла Маша? 5 – 1 = 4 (гр.)

Колькі ўсяго фруктаў купіла Маша?

1. 5 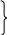- 1=4 (гр.) 2) 5 + 4=9 (фр.)

К ароткі запіс: Б.- 5 Усяго-? фр.

Гр. -?, на 1 менш, чым

Рашэнне задачы састаўленнем выразу: 5 + (5 – 1) = 9 (фр.).

2-і варыянт

Задачу можна перафармуляваць у другую з трыма дадзенымі: Маша купіла 5 бананаў і 4 грушы, 3 фрукты аддала маме. Колькі фруктаў засталося ў Машы?

Гэта задача на два дзеянні. Яна мае некалькі рашэнняў.

1-ы спосаб: 1) 5+4=9 (фр.) 2) 9- 3=6 (фр.) (5+4)-3= 6 (фр.)

2-і спосаб: ( 5 – 3 ) + 4 = 6 (фр.) Спачатку задача раша-

3-і спосаб: 5 + ( 3 – 2 )= 6 (фр.) ецца па дзеяннях.

Для замацавання прапануюцца заданні:

1.Дадзена ўмова задачы: Коля знайшоў 6 падасінавікаў, а падбярозавікаў на 4 больш. Паставіць да ўмовы пытанні, каб задача рашалася: 1) на адно дзеянне, 2) на два дзеянні. 2. Зрабіць кароткія запісы састаўленых задач.