Момент инерции

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси: В случае непрерывного распределения масс эта сумма сводится к интегралу где интегрирование производится по всему объему тела. При этом величина r в есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1).

Рис.1

Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции отдельного полого цилиндра dJ=r²dm (так как dr<<r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm - масса всего элементарного цилиндра; его объем 2πrhdr. Если ρ-плотность материала, то dm=2πrhρdr и dJ=2πhρr³dr. Тогда момент инерции сплошного цилиндра

но так как πR2h - объем цилиндра, то его масса m=πR2hρ, а момент инерции Если мы знаем момент инерции тела относительно оси, проходящей через его центр масс, то мы можем найти и момент инерции относительно любой другой параллельной этой оси, который можно найти с помощью теоремы Гюйгенса-Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями: Приведем значения моментов инерции (табл. 1) для некоторых тел (тела считаются однородными, m - масса тела).

Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси.

При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения.

Момент инерции твердого тела - это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.

Формула момента инерции:

Единица момента инерции - килограмм-метр в квадрате.

Теорема Штейнера:

Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями.

Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции тела относительно некоторой оси.

6.) Кинетическая энергия вращения. Закон сохранения момент импульса.

Возьмем абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него (рис. 1). Разобьем тело на маленькие объемы с элементарными массами m₁, m₂,..., m_n , находящиеся на расстоянии r₁, r₂,..., r_n от оси.

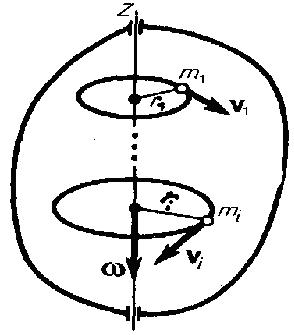
Рис.1

При вращении твердого тела относительно неподвижной оси каждый из его элементарных объемов массами m_i опишет окружность соответствующих радиусов r_i; при этом объем будет иметь соответствующую линейную скорость v_i. Но так как мы рассматриваем абсолютно твердое тело, то угловая скорость вращения этих объемов одинакова: (1) Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов: или Используя выражение (1), получаем где J_z - момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела (2) Из сравнения формулы (2) с выражением для кинетической энергии поступательно движущегося тела (T=mv²/2), мы видим, что момент инерции является мерой инертности тела при вращательном движении. Формула (2) справедлива для тела вращающегося вокруг неподвижной оси. В качеcтве примера напишем формулу для плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения. Его энергия движения складывается из энергии поступательного движения и энергии вращения: где m - масса катящегося тела; v_c - скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс; ω - угловая скорость тела.

Закон сохранения момент импульса.

Выводя закон сохранения импульса, введем следующие понятия. Множество материальных точек (или тел), рассматриваемых нами как единое целое, называется механической системой. Внутренние силы - силы взаимодействия между материальными точками механической системы. Внешние тела действуют на материальные точки системы с некоторыми внешними силами. Механическая система тел, называется замкнутой (или изолированной), если сумма всех действующих на нее внешних сил равна нулю. В механической системе, состоящей из нескольких тел, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположнs по направлению, значит векторная сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, с массами m₁, m₂, ... , m_n и скоростями v₁, v₂, ... , v_n. Пусть F₁^', F₂^', ... , F_n^' - равнодействующие внутренних сил, действующих на каждое из n тел, a F₁^', F₂^', ... , F_n^' - равнодействующие внешних сил. Применим второй закон Ньютона для каждого из n тел рассматриваемой механической системы: ... Складывая почленно эти уравнения, получаем Но так как векторная сумма внутренних сил механической системы равна нулю по третьему закону Ньютона, то или (1) где

- импульс механической системы. Значит, производная по времени от импульса механической системы равна векторной сумме внешних сил, действующих на систему. В случае замкнутой системы: т.е. (2) Выражение (2) есть закон сохранения имаульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Эксперименты доказывают, что закон сохранения импульса выполняется и для замкнутых систем микрочастиц, несмотря на то, что они подчиняются законам квантовой механики, т.е. этот закон носит универсальный характер, т. е. закон сохранения импульса - фундаментальный закон природы.