49.Радиоактивность. Закон радиоактивного распада. Виды радиоактивных излучений.

Радиоактивность (от лат. radio — излучаю, radius — луч и activus — действенный), самопроизвольное (спонтанное) превращение неустойчивого изотопа химического элемента в другой изотоп (обычно — изотоп другого элемента).

Закон радиоактивного распада — закон, открытый Фредериком Содди и Эрнестом Резерфордом экспериментальным путём и сформулированный в 1903 году. Современная формулировка закона:

что означает, что число распадов за интервал времени t в произвольном веществе пропорционально числу имеющихся в образце атомов N.

В этом математическом выражении лямбда — постоянная распада, которая характеризует вероятность радиоактивного распада за единицу времени и имеющая размерность с−1. Знак минус указывает на убыль числа радиоактивных ядер со временем.

Этот закон считается основным законом радиоактивности, из него было извлечено несколько важных следствий, среди которых формулировки характеристик распада — среднее время жизни атома и период полураспада.

Группа корпускулярных излучений

альфа-излучение (поток альфа-частиц (ядер гелия)),

бета-излучение (поток бета-частиц (электронов)),

нейтронное излучение (поток нейтронов).

Группа волновых излучений

гамма-излучение (поток гамма-квантов (фотонов)),

рентгеновские излучения (икс-лучи).

50.Элементарные частицы. Их основные характеристики. Виды взаимодействий. Классификация и свойства частиц. Теория кварков и идеи объединения фундаментальных взаимодействий.

Элемента́рная части́ца — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части.

Общими характеристиками всех Э. ч. являются масса (m), время жизни (t), спин (J) и электрический заряд (Q). Пока нет достаточного понимания того, по какому закону распределены массы Э. ч. и существует ли для них какая-то единица измерения.

Классификация:

По величине спина

Все элементарные частицы делятся на два класса:

бозоны — частицы с целым спином (например, фотон, глюон, мезоны).

фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино);

По видам взаимодействий

Элементарные частицы делятся на следующие группы:

Составные частицы

адроны — частицы, участвующие во всех видах фундаментальных взаимодействий. Они состоят из кварков и подразделяются, в свою очередь, на:

мезоны — адроны с целым спином, то есть являющиеся бозонами;

барионы — адроны с полуцелым спином, то есть фермионы. К ним, в частности, относятся частицы, составляющие ядро атома, — протон и нейтрон.

Фундаментальные (бесструктурные) частицы

лептоны — фермионы, которые имеют вид точечных частиц (т. е. не состоящих ни из чего) вплоть до масштабов порядка 10−18 м. Не участвуют в сильных взаимодействиях. Участие в электромагнитных взаимодействиях экспериментально наблюдалось только для заряженных лептонов (электроны, мюоны, тау-лептоны) и не наблюдалось для нейтрино. Известны 6 типов лептонов.

кварки — дробнозаряженные частицы, входящие в состав адронов. В свободном состоянии не наблюдались (для объяснения отсутствия таких наблюдений предложен механизм конфайнмента). Как и лептоны, делятся на 6 типов и считаются бесструктурными, однако, в отличие от лептонов, участвуют в сильном взаимодействии.

калибровочные бозоны — частицы, посредством обмена которыми осуществляются взаимодействия:

фотон — частица, переносящая электромагнитное взаимодействие;

восемь глюонов — частиц, переносящих сильное взаимодействие;

три промежуточных векторных бозона W+, W− и Z0, переносящие слабое взаимодействие;

гравитон — гипотетическая частица, переносящая гравитационное взаимодействие. Существование гравитонов, хотя пока не доказано экспериментально в связи со слабостью гравитационного взаимодействия, считается вполне вероятным; однако гравитон не входит в Стандартную модель элементарных частиц.

Адроны и лептоны образуют вещество. Калибровочные бозоны — это кванты разных типов взаимодействий.

Кроме того, в Стандартной модели с необходимостью присутствует хиггсовский бозон, который, впрочем, пока ещё не обнаружен экспериментально.

Согласно современным представлениям, в природе осуществляется четыре типа фундаментальных взаимодействий: сильное, электромагнитное, слабое и гравитационное.

Сильное, или ядерное, взаимодействие обусловливает связь протонов и нейтронов в ядрах атомов и обеспечивает исключительную прочность этих образований, лежащую в основе стабильности вещества в земных условиях.

Электромагнитное взаимодействие характеризуется как взаимодействие, в основе которого лежит связь с электромагнитным полем. Оно характерно для всех элементарных частиц, за исключением нейтрино, антинейтрино и фотона. Электромагнитное взаимодействие, в частности, ответственно за существование атомов и молекул, обусловливая взаимодействие в них положительно заряженных ядер и отрицательно заряженных электронов.

Слабое взаимодействие — наиболее медленное из всех взаимодействий, протекающих в микромире. Оно ответственно за взаимодействие частиц, происходящих с участием нейтрино или антинейтрино (например, b-распад, m-распад), а также за безнейтринные процессы распада, характеризующиеся довольно большим временем жизни распадающейся частицы (t>=10^-10 с).

Гравитационное взаимодействие присуще всем без исключения частицам, однако из-за малости масс элементарных частиц оно пренебрежимо мало и, по-видимому, в процессах микромира несущественно.

Кварки - это гипотетические материальные объекты, их экспериментальное наблюдение пока невозможно, однако теоретические положения кварковой гипотезы оказались плодотворными, а теория в целом эвристичной. Кварки представляют собой истинно элементарные частицы и поэтому бесструктурны. Главная особенность кварков - дробный заряд.

Кварки различаются спином, ароматом и цветом. Аромат кварка-это его особая физическая характеристика. Для того чтобы учесть все известные адроны, необходимо было предположить существование шести видов кварков, различающихся ароматом: u (up - верхний), d (down - нижний), s (strange - странный), c (charm - очарование), b (beauty - прелесть) и t(top - верхний). Существует устойчивое мнение, что кварков не должно быть больше. Считается, что каждый кварк имеет один из трех возможных цветов, которые выбраны произвольно: красный, зеленый, синий. Цвет кварка, как и аромат, - условное название для определенной физической характеристики.

Каждому кварку соответствует антикварк с противоположным цветом (антикрасный, антизеленый и антисиний). Кварки соединяются тройками, образуя барионы (нейтрон, протон), или парами, образуя мезоны. Антикварки, соединясь тройками, соответственно, образуют антибарионы. Мезон состоит из кварка и антикварка. Суммарный цвет объединившихся кварков или антикварков, независимо от того, объединены три кварка (барионы), три антикварка (антибарионы) или кварк и антикварк (мезоны), должен быть белым или бесцветным. Белый цвет дает сумма красного, зеленого, синего или красного - антикрасного, синего - антисинего и т.п. Кварки объединяются между собой благодаря сильному взаимодействию. Переносчиками сильного взаимодействия выступают глюоны, которые как бы "склеивают" кварки между собой. Глюоны также имеют цвета, но в отличие от кварков их цвета смешанные, например красный - антисиний и т.п., т.е. глюон состоит из цвета и антицвета. Испускание или поглощение глюона меняет цвет кварка, но сохраняет аромат. Известно восемь типов глюонов.

ВЗАИМОДЕЙСТВИЯ

Первой из теорий взаимодействий стала теория электромагнетизма, созданная Максвеллом в 1863 году. Затем в 1915 г. Эйнштейн сформулировал общую теорию относительности, описывающую гравитационное поле. Появилась идея построения единой теории фундаментальных взаимодействий (которых на тот момент было известно только два), подобно тому как Максвеллу удалось создать общее описание электрических и магнитных явлений. Такая единая теория объединила бы гравитацию и электромагнетизм в качестве частных проявлений некоего единого взаимодействия.

В течение первой половины XX века ряд физиков предприняли многочисленные попытки создания такой теории, однако ни одной полностью удовлетворительной модели выдвинуто не было. Это, в частности, связано с тем, что общая теория относительности и теория электромагнетизма различны по своей сути. Тяготение описывается искривлением пространства-времени, и в этом смысле гравитационное поле нематериально, в то время как электромагнитное поле является материей

Во второй половине XX столетия задача построения единой теории осложнилась необходимостью внесения в неё слабого и сильного взаимодействий, а также квантования теории.

В 1967 году Саламом и Вайнбергом была создана теория электрослабого взаимодействия, объединившая электромагнетизм и слабые взаимодействия. Позднее в 1973 году была предложена теория сильного взаимодействия (квантовая хромодинамика). На их основе была построена Стандартная Модель элементарных частиц, описывающая электромагнитное, слабые и сильное взаимодействия.

Экспериментальная проверка Стандартной Модели заключается в обнаружении предсказанных ею частиц и их свойств. В настоящий момент открыты все элементарные частицы Стандартной Модели, за исключением хиггсовского бозона.

Таким образом, в настоящее время фундаментальные взаимодействия описываются двумя общепринятыми теориями: общей теорией относительности и Стандартной Моделью. Их объединения пока достичь не удалось из-за трудностей создания квантовой теории гравитации. Для дальнейшего объединения фундаментальных взаимодействий используются различные подходы: теории струн, петлевая квантовая гравитация, а также М-теория.

1. Свободные незатухающие колебания. Энергия и импульс гармонического осциллятора. Фазовая траектория. Физический маятник.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной.

ФАЗОВАЯ ТРАЕКТОРИЯ - кривая в фазовом пространстве, составленная из точек, представляющих состояние динамической системы в последоват. моменты времени в течение всего времени эволюции.

*** Гармоничным осциллятором называется физический объект, эволюция которого со временем описывается дифференциальным уравнением

где q – обобщенная координата гармонического осциллятора, t – время, ? – характерная частота гармонического осциллятора. Две точки над переменной означают вторую производную по времени. Величина q совершающий гармонические колебания. Большое количество физических систем ведут себя как гармоничные осциллятора при малом отклонении от равновесия. К ним относятся математический и физический маятники, колебания атомов в молекулах и твердых телах, электрические колебательные контуры и многие другие.

Кинетическая энергия гармонического осциллятора задается выражением

Потенциальная энергия гармонического осциллятора задается выражением

Обобщенный импульс линейного гармонического осциллятора:

Свободные колебания всегда затухают из-за потерь энергии (трение, сопротивление среды, сопротивление проводников электрического тока и т. п.).Незатухающие колебания создаются такими устройствами, которые сами могут поддерживать свои колебания за счет некоторого постоянного источника энергии. Такие устройства называются автоколебательными системами. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Внешний источник периодического воздействия обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

2. Свободные затухающие колебания. Время релаксации. Декремент и логарифмический декремент затухания. Добротность колебательной системы.

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

где: f₀ — резонансная частота колебаний W — энергия, запасённая в колебательной системе P_d — рассеиваемая мощность.

      

      Время релаксации τ – время, в течение которого амплитуда А уменьшается в   e    раз.

      Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.

      Пусть N число колебаний, после которых амплитуда уменьшается в e  раз. Тогда

                  ;              ;

      Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. Если χ = 0,01, то N = 100.

      При большом коэффициенте затухания происходит не только быстрое уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда сопротивление становится равным критическому, а то круговая частота обращается в ну олебания прекращаются. Такой процесс называется апериодическим

   Отличия в следующем. При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.

Релаксация— процесс установления термодинамического, а следовательно, и статистического равновесия в физической системе, состоящей из большого числа частиц.

Время релаксации – промежуток времени, в течение которого выведенная из равновесия система возвращается в состояние термодинамического равновесия. Отсюда:

– средняя скорость релаксации.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида

в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются.

3. Вынужденные колебания. Установившиеся вынужденные колебания. Механический резонанс.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Вынужденные колебания изменяется со временем (в частности, Вынужденные колебания не являются периодическими), и лишь по прошествии некоторого времени в системе устанавливаются периодические Вынужденные колебания с периодом, равным периоду внешней силы (установившиеся Вынужденные колебания). Установление Вынужденные колебания в колебательной системе происходит тем быстрее, чем больше затухание колебаний в этой системе.

Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

4. Упругие волны. Стоячие волны. Волновое уравнение. Эффект Доплера.

Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве.

Упругая волна - это процесс распространения колебаний в упругой среде. Характерное свойство волны - перенос энергии без переноса вещества.

Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана.

Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длина уменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.

5. Плоская гармоническая волна. Амплитуда, частота, фаза, длина волны. Фазовая скорость волны. Сферические волны. Поляризация волн.

наиболее важным и часто встречающимся типом гармонических волн являются плоские гармонические волны. (Одномерные гармонические волны являются их одномерным частным случаем.)

• Бегущая плоская волна — это волна такого вида:

или

где, в отличие от одномерной волны

 — уже не действительное число, а вектор, называемый волновым вектором, размерность которого равна размерности пространства, а выражение

означает скалярное произведения этого вектора с вектором

, характеризующим точку пространства:

.

Легко видеть, что если выбрать ось координат вдоль волнового вектора, плоская многомерная волна сводится к одномерной (u вообще перестает зависеть от остальных координат, а от первой — зависит как одномерная гармоническая волна).

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой λ

ЧАСТОТА ВОЛНЫ, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в ГЕРЦАХ.

Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.

Фа́за колеба́ний — физическая величина, при заданной амплитуде и коэффициенте затухания, определяющая состояние колебательной системы в любой момент времени. Фаза обычно выражается в угловых единицах (радианах, градусах) или в циклах (долях периода):1 цикл = 2π радиан = 360 градусов.

Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы). Ее можно рассматривать при желании как векторную величину.

Наиболее употребительное обозначение:

.

сферическая волна — поверхностью равных фаз является сфера

Поляриза́ция волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического и магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения

6. Гармонические колебания. Сложение гармонических колебаний одного направления равных и близких частот. Векторная диаграмма. Биения.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Уравнение гармонических колебаний имеет вид:

, где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия)

;

- круговая (циклическая) частота.

При сложении двух гармонических колебаний одинакового направления и частоты, результирующее смещение будет суммой

( )

Смещений

и

, которые запишутся следующими выражениями:

, ,

Сумма двух гармонических колебаний также будет гармоническим колебанием той же круговой частоты:

= . Значения амплитуды А и начальной фазы φ этого гармонического колебания будет зависеть от амплитуд исходных колебаний и их начальных фаз

На рисунке 1.2. приведено два примера А и В сложения гармонических колебаний с использованием метода векторных диаграмм. Из векторных диаграмм видно, что направление (начальная фаза φ) и длина А вектора амплитуды суммарного гармонического колебания зависит, как от направления (от начальных фаз), так и от длины векторов амплитуд исходных гармонических колебаний. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен 0, то исходные колебания находятся в фазе и суммарная амплитуда (А =А1 +А2) будет максимальна. Если угол (разность фаз: Δφ = φ1 - φ2) между векторами А1 и А2 равен - π или π, то исходные колебания находятся в противофазе и суммарная амплитуда (А = А1 -А2 ) будет минимальна

Биения возникают при сложении колебаний, отличающихся по частоте на небольшую величину, и проявляются в появлении более низкочастотных изменений амплитуды суммарного сигнала, по сравнению с исходными частотами. Амплитуда колебаний при этом меняется от минимального значения равного разности исходных амплитуд до максимального значения, равного сумме амплитуд исходных колебаний, и вновь до минимального значения. Периодом биений является время повторения этого процесса (Рис 1.3.).

Рисунок 1.3. Биения

За счет того, что вращение векторов А1 и А2 происходит с близкими, но отличающимися скоростями, разность фаз этих двух колебаний будет не постоянна, а медленно, то увеличиваться, то уменьшаться. Колебания будут находиться, то в фазе, то в противофазе, в результате амплитуда суммарного сигнала тоже будет меняться. Время за которое разность фаз измениться на 2π и будет периодом биений Тб (Тб = 2π/Δω). Δω -разность круговых частот исходных колебаний. Биения применяют при обнаружении металлических предметов мин, оружия и т.д. Для этого используют два одинаковых высокочастотных колебательных контура, имеющих одинаковую частоту. Если вблизи одного из них появится металлический предмет, частота этого контура немного изменится. При сложении сигналов от этих двух контуров, в суммарном сигнале возникнет низкочастотная составляющая. Ее можно выделить и подать в наушники, в которых возникнут звуковые колебания, сигнализирующие о наличии металлического предмета.

7. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот. Фигуры Лиссажу.

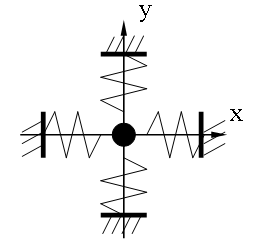
Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости. По какой траектории будет двигаться это тело?

Это уравнения траектории в параметрическом виде. Для получения явной зависимости между координатами x и y надо из уравнений исключить параметр t.

Из первого уравнения:

;      

     .

Из второго:

.

После подстановки: 

     .

Избавимся от корня:

.

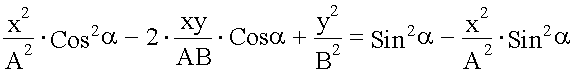- это уравнение эллипса.

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π вырождаются в отрезки прямых, а при разности фаз

и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

8. Интерференция света. Методы наблюдения. Условия образования максимумов и минимумов при интерференции. Методы получения когерентных источников света.

Интерференция света — нелинейное сложение интенсивностей двух или нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. При интерференции света происходит перераспределение энергии в пространстве.

Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.

Зеркала Френеля. Свет от источника S (рис. 246) падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол  мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S₁ и S₂ (угловое расстояние между которыми равно 2) лежат на одной и той же окружности радиуса r с центром в О (точка соприкосновения зеркал).

Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S₁ и S₂, являющихся мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂ взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2. Интерференционная карти­на наблюдается на экране (Э), защищенном от прямого попадания света заслон­кой (З).

Метод Юнга. Источником света служит ярко освещенная щель S (рис. 245), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников.

Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S₁ и S₂. Как уже указывалось, Т. Юнгу принадлежит первое наблюдение явления интерференции.

Условия образования максимумов и минимумов в интерференционной картине. Результат сложения волн, приходящих в точку наблюдения М от двух когерентных источников О₁ и О₂ зависит от разности фаз между ними (см. рис 1.)

рис. 1.

Расстояния, проходимые волнами от источников до точки наблюдения, равны соответственно d₁и d₂. Величина называется геометрической разностью хода d = d₂- d₁. Эта величина и определяет разность фаз колебаний в точке М. Возможны два предельных случая наложения волн.

Для получения когерентных источников света французский физик Огю-стен Френель (1788—1827) нашел в 1815 г. простой и остроумный способ. Надо свет от одного источника разделить на два пучка и, заставив их пройти различные пути, свести вместе. Тогда цуг волн, испущенных отдельным атомом, разделится на два когерентных цуга. Так будет для цугов волн, испускаемых каждым атомом источника. Свет, испускаемый одним атомом, дает определенную интерференционную картину. При наложении этих картин друг на друга получается достаточно интенсивное распределение освещенности на экране: интерференционную картину можно наблюдать. Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны. Для этого используют два зеркала (бизеркала Френеля), бипризму (две призмы, сложенные основаниями), билинзу (разрезанную пополам линзу с раздвинутыми половинами) и др.

9. Дифракция света. Принцип Гюйгенса-Френеля. Метод зон Френеля. Пятно Пуассона.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.

Принцип Гюйгенса–Френеля также представлял собой определенную гипотезу, но последующий опыт подтвердил ее справедливость. В ряде практически важных случаев решение дифракционных задач на основе этого принципа дает достаточно хороший результат. Рис. 3.8.1 иллюстрирует принцип Гюйгенса–Френеля.

Рисунок 3.8.1. Принцип Гюйгенса–Френеля. ΔS1 и ΔS2 – элементы волнового фронта, и – нормали

Пусть поверхность S представляет собой положение волнового фронта в некоторый момент. В теории волн под волновым фронтом понимают поверхность, во всех точках которой колебания происходят с одним и тем же значением фазы (синфазно). В частности, волновые фронта плоской волны – это семейство параллельных плоскостей, перпендикулярных направлению распространения волны. Волновые фронта сферической волны, испускаемой точечным источником – это семейство концентрических сфер.

Для облегчения расчета Френель предложил разбить волновую поверхность падающей волны в месте расположения препятствия на кольцевые зоны (зоны Френеля) по следующему правилу: расстояние от границ соседних зон до точки P должны отличается на половину длины волны, т. е.

Если смотреть на волновую поверхность из точки P, то границы зон Френеля будут представлять собой концентрические окружности (рис. 3.8.3).

Рисунок 3.8.3. Границы зон Френеля в плоскости отверстия

Из рис. 3.8.2 легко найти радиусы ρ_m зон Френеля:

Так в оптике λ << L, вторым членом под корнем можно пренебречь. Количество зон Френеля, укладывающихся на отверстии, определяется его радиусом R:

Здесь m – не обязательно целое число. Результат интерференции вторичных волн в точке P зависит от числа m открытых зон Френеля. Легко показать, что все зоны имеют одинаковую площадь:

Одинаковые по площади зоны должны были бы возбуждать в точке наблюдения колебания с одинаковой амплитудой. Однако у каждой последующей зоны угол α между лучом, проведенным в точку наблюдения, и нормалью к волновой поверхности возрастает. Френель высказал предположение (подтвержденное экспериментом), что с увеличением угла α амплитуда колебаний уменьшается, хотя и незначительно:

A1 > A2 > A3 > ... > A1,

где A_m – амплитуда колебаний, вызванных m-й зоной.

С хорошим приближением можно считать, что амплитуда колебаний, вызываемых некоторой зоной, равна среднему арифметическому из амплитуд колебаний, вызываемых двумя соседними зонами, т. е.

Так как расстояния от двух соседних зон до точки наблюдения отличаются на λ / 2, следовательно, возбуждаемые этими зонами колебания находится в противофазе. Поэтому волны от любых двух соседних зон почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть

A = A1 – A2 + A3 – A4 + ... = A1 – (A2 – A3) – (A4 – A5) – ... < A1.

Таким образом, суммарная амплитуда колебаний в точке P всегда меньше амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В частности, если бы были открыты все зоны Френеля, то до точки наблюдения дошла бы невозмущенная препятствием волна с амплитудой A₀. В этом случае можно записать:

так как выражения, стоящие в скобках, равны нулю. Следовательно, действие (амплитуда), вызванное всем волновым фронтом, равно половине действия одной первой зоны.

Итак, если отверстие в непрозрачном экране оставляет открытой только одну зону Френеля, то амплитуда колебаний в точке наблюдения возрастает в 2 раза (а интенсивность – в 4 раза) по сравнению с действием невозмущенной волны. Если открыть две зоны, то амплитуда колебаний обращается в нуль. Если изготовить непрозрачный экран, который оставлял бы открытыми только несколько нечетных (или только несколько четных) зон, то амплитуда колебаний резко возрастет. Например, если открыты 1, 3 и 5 зоны, то

A = 6A0, I = 36I0.

Такие пластинки, обладающие свойством фокусировать свет, называются зонными пластинками.

При дифракции света на круглом диске закрытыми оказываются зоны Френеля первых номеров от 1 до m. Тогда амплитуда колебаний в точке наблюдения будет равна

или A = A_m + 1 / 2, так как выражения, стоящие в скобках, равны нулю.

Если диск закрывает зоны не слишком больших номеров, то A_m + 1 ≈ 2A₀ и A ≈ A₀, т. е. в центре картины при дифракции света на диске наблюдается интерференционный максимум. Это – так называемое пятно Пуассона, оно окружено светлыми и темными дифракционными кольцами.

10. Уравнения Максвелла. Вектор Умова-Пойнтинга.

Объяснение и создание математической модели физического процесса или явления далеко не всегда можно решить «в лоб». Зачастую, приходиться вводить к основным понятиям некоторые дополнительные аргументы, чтобы показать функцию во всей красе.

Один из ярких примеров такого подхода может служить введение Максвеллом понятия тока смещения. Это позволило ему завершить созданную им теорию электромагнитного поля, которая позволила не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат четыре уравнения. 1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (EB), поэтому напряженность суммарного поля E = EQ + EB. Так как циркуляция вектора EQ равна нулю             а циркуляция вектора EB определяется выражением             то циркуляция вектора напряженности суммарного поля

[1]

             

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора H            

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D             Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ, то формула [3] запишется в виде              4. Теорема Гаусса для поля B              Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):              

где ε0 и μ0 – соответственно электрическая и магнитная постоянная, ε и μ – соответственно диэлектрическая и магнитная проницаемость, γ – удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных. Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид:

           

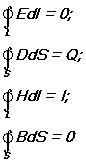
т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля. Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

           

можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

            

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла – интегральная и дифференциальная – эквивалентны. Однако если имеются поверхности разрыва (поверхности, на которых свойства среды или полей меняются скачкообразно), то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняю граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия

            

Первое и последнее уравнение отвечают случаям, когда на границе раздела двух сред нет ни свободных зарядов, ни токов проводимости.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.

Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компонент тензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:

(в системе СГС),

(в системе СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно.

(в комплексной форме)^[1],

где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно.

Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.

Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то вектор S непрерывен на границе двух сред.