27)Намагниченность вещества. Вектор напряженности магнитного поля и его связь с векторами индукции и намагниченности. Магнитные свойства веществ.

Намагниченность вещества - это векторная величина, равная объемной плотности магнитного дипольного момента в некоторой точке вещественного тела. Обозначается обычно М или J.

, Здесь, M — вектор намагниченности; m вектор магнитного момента; V — объём. (А\м)

Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. (А\м)

, где μ0 - магнитная постоянная.

Одно из первых обширных и систематических исследований магнитных свойств вещества было предпринято П.Кюри. Он установил, что по своим магнитным свойствам все вещества можно разделить на три класса. К первому относятся вещества с резко выраженными магнитными свойствами, подобными свойствам железа. Такие вещества называются ферромагнитными; их магнитное поле заметно на значительных расстояниях (см. выше). Во второй класс попадают вещества, называемые парамагнитными; магнитные свойства их в общем аналогичны свойствам ферромагнитных материалов, но гораздо слабее. Например, сила притяжения к полюсам мощного электромагнита может вырвать из ваших рук железный молоток, а чтобы обнаружить притяжение парамагнитного вещества к тому же магниту, нужны, как правило, очень чувствительные аналитические весы. К последнему, третьему классу относятся так называемые диамагнитные вещества. Они отталкиваются электромагнитом, т.е. сила, действующая на диамагнетики, направлена противоположно той, что действует на ферро- и парамагнетики.

28)Закон Ампера. Магнитный момент контура с током. Контур с током в магнитном поле. Поток вектора магнитной индукции.

Зако́н Ампе́ра — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила

, с которой магнитное поле действует на элемент объёма dV проводника с током плотности

, находящегося в магнитном поле с индукцией

:

Модуль силы Ампера можно найти по формуле:

,

где α — угол между векторами магнитной индукции и тока.

Сила

,

с которой магнитное поле действует на элемент

проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины

проводника на магнитную индукцию

:

.

Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Магнитный момент измеряется в А⋅м2 или Дж/Тл (СИ).

Поскольку в каждой из противоположных сторон контура действует самостоятельная сила Ампера, то за площадь для суммарного момента сил принимается не половина, а вся площадь контура. Тогда вводится понятие магнитного момента контура с током как собственной характеристики контура, которая численно равна произведению P=IS, где S это вся площадь контура. Направление магнитного момента задается нормалью контура с током

.

Тогда полный момент силы, действующий на контур с током в магнитном поле, численно равен:

.

Контур с током.Пусть в однородное магнитное поле помещена рамка с током (рисунок см. ниже). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором

и нормалью к площади

:

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

Это выражение также можно использовать для определения индукции магнитного поля:

Величину, равную произведению , называют магнитным моментом контура Рт. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

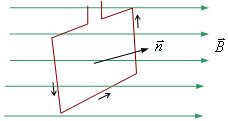
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна

,где Bn=Вcosα - проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В), dS=dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.