АГУЛЬНАЯ ХАРАКТАРЫСТЫКА ПАНЯЦЦЯ ЗАДАЧЫ

План

1. Паняцце задачы. Задача як мадэль праблемнай сітуацыі.\

2. Класіфікацыя простых задач.

3. Паняцце практычнай і вучэбнай задачы.

4 Методыка навучання рашэнню простых задач.

.

Літаратура

1.Качалко, в. Б. Поисково-исследовательская технология начального обучения математике / в.Б. Качалко. – Мозырь: уо мгпу им. И.П. Шамякина, 2008.—124 с. Гл.2 .

2.Загвязинский, В.И. Методология и методика дидактического исследования / В.И. Загвязинский. – М.: Высшая школа, 2002. – 142 с Ключавыя словы: праблемная сітуацыя, практычная і вучэбная задача, прамая і ўскосная, прыведзеная і непрыведзеная задача, мадэль задачы, прыёмы, метады і планы пошуку задачы.

ХАРАКТАРЫСТЫКА ПАНЯЦЦЯ “ЗАДАЧА”

Заданне, якое мае ўмову і патрабаванне, што патрэбна зрабіць, называюць задачай. Прыклады: 1) Вылічыць 9-2.

2) Рашыць няроўнасць 2+Х<9.

3) Пабудаваць квадрат, перыметр якога

роўны 16 см.

Найбольш характэрны для матэматыкі тэкставыя або сюжэтныя задачы: На адну талерку паклалі 20 вішань, што ў 2 разы больш,чым на другую (умова задачы). Колькі ўсяго вішань паклалі на талеркі ? (пытанне задачы)”.

З тэкста задачы звычайна выдзяляюць:

ПРАДМЕТНУЮ ВОБЛАСЦЬ: дзве талеркі з вішнямі. ВЕЛІЧЫНІ --колькасць.

ЗНАЧЭНННІ ВЕЛІЧЫНІ: вядомыя — 20 вішань, невядомыя – 10 в., шукаемае--30 в. АДНОСІНА: у 2 разы больш.

ЗАЛЕЖНАСЦЬ: усяго.

РАШЭННЕ: (20:2)+20=30 (в.).

АДКАЗ: паклалі 30 вішань на дзве талеркі.

ПО ФРИДМАНУ Л.М. З А Д А Ч А –знаковая модель проблемной ситуации, осознанного интеллектуального затруднения, которое субъект \

хочет и может преодолеть.

Цель

Преграда, Объект

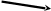
Деятельность затруднение

Озадаченный субьект

З

Мыслящий

предметная область (турист, скорость и др.) субъект

З отношения (>, <, = и др.)

А зависимости (v = s : t, цена = стоимость: на количество и др.)

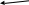
Д элементы постоянные ( 4 км, 5 ч. и др.)

А задачи переменные (v, s и др.)

Ч

А

известные неизвестные (промежуточные, искомые)

требование (вопрос)

оператор (а:в+с и др.)

Патрэбна адрозніваць паняцце “рашэнне задачы”:

1) як вынік (адказ-30 в.);

2) як спосаб рашэння задачы (а:2+а);

3) як працэс пошуку спосабу рашэння задачы;

4) як план знаходжання адказу.

Рашэнне задачы можна зрабіць рознымі спосабамі:

1.ПРАКТЫЧНЫМ –- з дапамогай канкрэтных прадметаў, напрыклад, палачак, кружкой і інш.;

2.АРЫФМЕТЫЧНЫМ -- рашэннем задачы па дзеяннях: 20:2=10 (в.); 10+20=30 (в.) або састаўленнем выразу: 20:2+10.

3.АЛГЕБРАІЧНЫМ - з дапамогай ураўнення:

х–20:2=20.

4. ГЕАМЕТРЫЧНЫМ – напрыклад,з дапамогай чарцяжа.

У пачатковых класах рашаюць задачы:

1) у прамой і ва ўскоснай форме;

2) з поўнымі, недастаючымі або з лішнімі дадзенымі

3) прамыя і адваротныя задачы.

Праверка рашэння задачы праводзіцца:

1) прыкідкай выніку;

2) рашэннем задачы другім спосабам;

3) рашэннем адваротнай задачы;

4) адпаведнасцю рашэння ўмове задачы.

Задачы бываюць: простыя на адно дзеянне,

на два і больш дзеянняў – састаўныя:

з прыведзенымі дадзенымі, калі дадзеныя размеш-чаны у парадку рашэння задачы або непрыведзе-нымі дадзенымі, калі гэта не так.

КЛАСІФІКАЦЫЯ ПРОСТЫХ ЗАДАЧ.

ФУНКЦЫІ ЗАДАЧ У НАВУЧАННІ МАТЭМАТЫЦЫ

Найбольш вядомая класіфікацыя простых задач:

1-ая група (5 відаў) - на знаходжанне:

1) сумы; 2) астатка; 3) сумы аднолькавых складаемых (здабытку); 4) дзяленне на роўныя часткі Пр.: Паклалі 8 груш пароўну на дзве талеркі. Колькі груш на кожнай талерцы? ; 5) дзяленне па зместу Пр.: Расклалі на талеркі 6 груш па 2 на кожную. Колькі талерак спатрэбілася?

2-ая група (8 відаў) - на сувязь паміж кампанентамі і вынікамі арыфметычных дзеянняў. Пр.: а) Купілі 3 сшыткі ў клетку і 5 – у лінейку. Колькі ўсяго купілі сшыткаў? б) Усяго купілі 8 сшыткаў у клетку і лінейку, з іх 3 сшыткі ў клетку. Колькі сшыткаў купілі ў лінейку? і інш..

3 - яя група (8 відаў) – на павялічэнне (памян-шэнне) ліку на некалькі адзінак і ў некалькі разоў ва ўскоснай і прамой форме. Пр.: а) Было 9 алоўкаў, што ў 3 разы больш, чым маркераў. Колькі было маркераў? (ускосная форма)

б) Было 9 алоўкаў, а маркераў- у 3 разы менш. Колькі было маркераў? (прамая форма).

4-я група (4 віды) – на параўнанне: рознаснае

( на колькі больш-менш) і на кратнае ( у колькі разоў больш-менш).

5-ая група (2 віды) -- на знаходжанне долі ад ліку і ліку па яго долі.

Пр.: а) Кілаграм цукерак каштуе 6 тысяч рублёў. Колькі каштуе 1/3 кг цукерак?

б) 1/3 кг цукерак каштуе 2 тысячы рублёў. Колькі каштуе 1 кг цукерак? або: Якая цана цукерак?

У пачатковым курсе матэматыкі задачы рашаюцца для:

1. засваення тэарэтычнага матэрыялу (плошча квадрата);

2. засваення прыёмаў арыфметычных вылічэнняў;

3. развіцця лагічнага мыслення (аналіз, аналогія і інш.);

4) маральнага і эстэтычнага выхавання вучняў;

5. кантролю ведаў, уменняў і навыкаў;

6. дыягностыкі разумовага развіцця вучняў.

ПАНЯЦЦЕ ПРАКТЫЧНАЙ І ВУЧЭБНАЙ ЗАДАЧЫ

Пачатковым этапам вучэбнай дзейнасці з’яўляецца пастаноўка вучэбнай задачя, адрозніваецца ад канкрэтна-практычнай задачы, у якой знаходзяць канкрэтны адказ, а не агульны спосаб рашэння ўсяго класа такіх задач. Як адзначае У.І Загвязінскі “Задача может превратиться в учебную только в том случае, если ученик самостоятельно или под руководством учи-теля осуществляет её переформулировку, чтобы найти обобщённый способ решения данного класса задач”.

Разгледзім задачу, спосаб рашэння якой вучні АШ №11 Мазыра павінны былі адкрыць. Гэта праблемная задача: З двух гарадоў, адлегасць паміж якімі 300км, адначасова насустрач адна адной выехалі дзве машыны. Хуткасць руху першай-55км/г, а хуткасцьдругой- - 45 км/г. Праз колькі гадзін машыны сустрэліся? Умоўныя абазначэнні:

S - пройдзеная адлегласць, V₁ , V₂ -хуткасці машын, t-час

1-ая г. !……… !……………………………………………!1-ая

2-ая гадз. 2-ая

3-яя гадзіна 3-яя

Гадзіна

Рашэнне практычнай задачы: 300:(55+45)=2(гадз.). Адказ адносіцца толькі да дадзенай задачы Такіх практычных задач рашаюць 5 -16,каб прыйсці да агульнага вываду.

Аднак можна пайсці па больш цяжкаму, але больш эфек-тыўнаму шляху на аснове эўрыстачнай гутаркі па чарцяжу, калі вучні прыходзяць да вываду: каб знайсці час у задачы на суст-рэчны рух, патрэбна падзяліць прой-дзеную адлегласць на суму хуткасцей рухаючыхся цел: t=S:(V₁+V₂). Вучні адкрылі агульны спосаб рашэння ўсіх задач на сустрэчны рух (знаходжанне часу руху). Гэта не толькі праблемная, але і вучэбная задача.

Тэарэтычныя асновы прымянення арыфметычных дзеянняў у рашэнні простых задач

Тэарэтычнай асновай СКЛАДАННЯ цэлых неадмоўных лікаў (ЦНЛ) з’яўляецца аперацыя аб’яднання А В=С канечных неперасякальных мностваў. Няхай колькасць элементаў п(А)=п{х,х,х}=3, п(В)=п{о,о}=2, тады п(С)=5, п(А В)=п{х,х,х,о,о}=3+2=5. . Тэарэтычнай асновай АДНІМАННЯ ЦНЛ з’яўляецца апе-рацыя рознасці мностваў С\А або С\В, дзе А С і В С. Тады п(С\А)=5-3=2, п(С\В)=5-2=3. . Тэарэтычнай асновай МНОЖАННЯ ЦНЛ з’яўляецца здабытак : 1) а•в=а+а+а+...+а (в разоў), 2) а•1=а, 3) а•0=0. Тэарэтычнай асновай ДЗЯЛЕННЯ ЦНЧ з’яўляецца разбіенне мноства А={х,х, о,о, *,*}, дзе п(А)=6, на роўнаколькасныя падмноствы: калі атрымоўваем колькасць элементаў кожнага падмноства 6:3=2, то гэта будзе дзяленне на роўныя часткі; калі атрымоўваем колькасць частак 6:2=3, то гэта будзе дзяленне па зместу.

ПОНЯТИЕ ЗАДАЧИ КАК МОДЕЛИ ПРОБЛЕМНОЙ СИТУАЦИИ.

З А Д А Ч А –знаковая модель проблемной ситуации, осознанного интеллектуального затруднения, которое субъект

хочет и может преодолеть.

Цель

Преграда, Объект

Деятельность затруднение

Озадаченный субьект

Мыслящий

предметная область (турист, скорость и др.) субъект

З отношения (>, <, = и др.)

А зависимости (v = s : t, цена = стоимость: на количество и др.)

Д элементы постоянные ( 4 км, 5 ч. и др.)

А задачи переменные (v, s и др.)

Ч

А

известные неизвестные (промежуточные, искомые)

требование (вопрос)

оператор (а:в+с и др.)

МЕТОДЫКА НАВУЧАННЯ РАШЭННЮ ПРОСТЫХ ЗАДАЧ: 1.НА СЭНС АРЫФМЕТЫЧНЫХ ДЗЕЯННЯЎ,

2.НА ЎЗАЕМАСУВЯЗЬ АРЫФМЕТЫЧНЫХ ДЗЕЯННЯў, 3.НА ПАВЯЛІЧЭННЕ (ПАМЯНШЭННЕ) ЛІКУ НА НЕКАЛЬКІ АДЗІНАК І Ў НЕКАЛЬКІ РАЗОЎ; 4.НА РОЗНАСНАЕ І КРАТНАЕ ПАРАЎНАННЕ; 5.НА РАШЭННЕ ЗАДАЧ У ПРАМОЙ І ВА ЎСКОСНАЙ ФОРМЕ. Асноўная: 1, гл.3 п.19 2, гл. 4. пп.4.3-4.4 Дадатковая: 3, гл.3, п.п. 1-2. В.Б., Качалко Метады актыўнага навучання матэматыцы ў пвчатковых класах / В. Б. Качалко.—Мінск; МГПУ ім. М. Горького, 1984 – 79 с.

Ключавыя словы: задачы ў прамой і ва ўскоснай форме, адваротныя задачы,састаўныя задакчы, разбор задачы,

Навучання рашэнню простых залач на сэнс арыфметычных дзеянняў

Простыя задачы на сэнс арыфметычных дзеянняў у пачатковых класах спачатку рашаюцца на канкрэтных мноствах з улікам аперацый над імі, а затым іх рашэнні запісваюцца з дапамагай лічбаў і матэматычных сімвалаў (+, --, •, :, =), пры гэтым уводзяцца назвы гэтых сімвалаў, а таксама назвы кампанентаў і вынікаў арыфметычных дзеянняў.

Простыя задачы на складанне

зручна ілюстраваць на прадметах з дапамогай наборнага палатна, напрыклад, задачу: Коля выразаў 3 квадраты і 2 кругі. Колькі ўсяго фігур выразаў Коля? Выстаўляюцца на палатне асобна ППП і ОО, а затым разам ПППОО. Пад кожным мноствам запісваецца яго колькасць (3,2,5). Гаворыцца: на матэматычнай мове рашэнне задачы запісваецца: 3+2=5, чытаецца: да трох прыкласці два будзе пяць або 3 плюс 2 роўна 5; 3 і 2 – складаемыя (1-ае і 2-ое), 5-сума, 3+2 – таксама сума лікаў.

Простыя задачы на адніманне

ўводзяцца аналагічна. Зручна гэта рабіць на задачах, адваротных задачам на складанне: Коля выразаў кругі і квадраты, усяго – 5. З іх 3 былі квдраты. Колькі кругоў выразаў Коля? На матэматычнай мове запісваецца 5-3=2, чытаецца: ад 5 адняць 3 атрымаецца 2 або 5 мінус 3 роўна 2; 5 - гэта памяншаемае, 3- аднімаемае, 2 – рознасць, 5-3 – таксама рознасць лікаў.

Простыя задачы на множанне

звязваюць са складаннем аднолькавых лікаў. Напрыклад, прапануецца задача: Вучань на 5 канвертаў наклеіў па 2 маркі. Колькі ўсяго марак наклеіў вучань? Гэта задача спачатку рашаецца складаннем: 2+2+2+2+2=10 (м.). Больш кароткі запіс рашэння з дапамогай новага дзеяння множання: 2•5=10, што чытаецца: па 2 узяць 5 разоў атрымаецца 10 або 2 памножыць на 5 роўна 10; 2 і 5 –множнікі (1-ы і 2-і), 10 - здабытак, 2•5 – здабытак лікаў.

Адрозніваюць дзяленне на роўныя часткі і дзяленне па зместу.

Лепш за ўсё адрозненне паміж гэтымі відамі дзялення паказаць на інсцэніроўцы. Аднаму з вучняў даецца 6 бананаў і прапануецца раскласці іх пароўну на двух талерках. Ён раскладвае іх па аднаму на талерку і атрымоўвае па 3 бананы на кожнай:

6 : 2= 3 (б.) (6 падзяліць на 2 роўныя часткі будзе па 3). Гэта задача на дзяленне на роўныя часткі.

Другому вучню прапануецца 12 бананаў раскласці на талеркі па 3 бананы на кожную, устанавіць, колькі талерак для гэтага спатрэбіцца. Ён прапануе 12 бананаў раскладваць па 3 групамі: 12-3–3-3-3=0 або 12 : 3 = 4 (т.) (12 падзяліць па 3 будзе 4). У далейшым чытаецца: 12 падзяліць на 3 роўна 4; 12- гэта дзялімае, 3-дзельнік, 4-дзель, 12:3–дзель лікаў. Гэта задача на дзяленне па зместу.