Лекция

Коды с выявлением ошибок

Появление одиночной ошибки в одном из разрядов 4-разрядного двоичного кода может привести к неправильному, но допустимому кодовому набору. Если код такой, что появление любой одиночной ошибки превращает допус­тимый кодовый набор в недопустимый кодовый набор, то его называют ко­дом с выявлением (одиночной) кодовой ошибки. Два таких кода приведены в табл. 1.5.

Выявление ошибки в любом из этих кодов проводится проверкой на чет­ность. Эта проверка основана на присоединении к каждому набору дополни­тельного разряда с тем, чтобы количество единиц в любом кодовом наборе данного кода было нечетным или четным. Более целесообразно число единиц в кодовом наборе с выявлением одиночной ошибки выбирать нечетным. То­гда любое кодовое представление, в том числе и для нуля, будет иметь хотя бы одну 1. Это даст возможность отличить полное отсутствие информации от передачи нуля в том случае, если 1 отражает наличие электрического сигна­ла, а 0 — его отсутствие.

Таблица 1-. Коды с выявлением ошибки

Десятичное число	Двоично-десятичный код с проверкой на четность					Код 2 из 5"
	8	4	2	1	р		0	1		2	4	7
0	0	0	0	0	0		0	0		0	1	1
1	0	0	0	1	1		1	1		0	0	0
2	0	0	1	0	1		1	0		1	0	0
Десятичное число	Двоично-десятичный код с проверкой на четность					Код "2 из 5"
3	0	0	1	1	0		0	1	1		0	0
4	0	1	0	0	1		1	0	0		1	0
5	0	1	0	1	0		0	1	0		1	0
6	0	1	1	0	0		0	0	1		1	0
7	0	1	1	1	1		1	0	0		0	1
8	1	0	0	0	1		0	1	0		0	1
9	1	0	0	1	0		0	0	1		0	1

Дополнительный разряд р называется контрольным разрядом четности. Код, который состоит из всех 10 возможных комбинаций 5-разрядных кодовых наборов с двумя единицами, называется кодом "2 из 5".

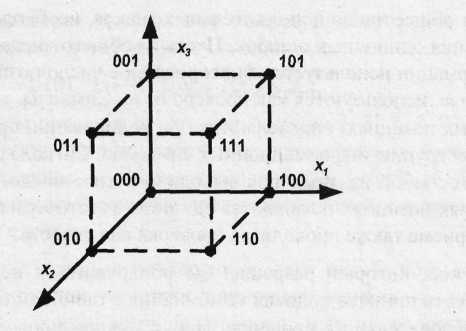
При построении корректирующих кодов часто прибегают к геометрической моде­ли. Допустим, есть алфавит, который состоит из трех символов. Из них можно со­ставить следующие комбинации: 000, 001, 010, 011, 100, 101, 110, 111. В трехмерном пространстве на осях найдем точки с координатами кода (рис. 1.1). Помеха может исказить сигнал, т. е. вместо 0 появится 1 или наоборот. Очевидно, что если кодовые комбинации отличаются одна от одной длиной ребра d = 1, то помеха переведет один сигнал в другой и обнаружить ошибку в этом случае нельзя. Ее можно обнаружить, если кодовые комбинации отстоят одна от одной на два ребра, т. е. 000, 011, 101, 110. Для исправления необходимо, чтобы комбинации отлича­лись на три единицы: 000, 111. Пространство, представленное на рис. 1.1, назы­вается пространством Хемминга, а величина d — расстоянием по Хеммингу или минимальным кодовым расстоянием. Например, минимальное кодовое расстояние для кодов из табл. 1.5 равняется двум. Очевидно, что это расстояние всегда целое число, равное числу разрядов, в которых отличаются двоичные числа, соответст­вующие точкам в пространстве Хемминга. В общем случае пространство Хеммин­га имеет n координат и изображается n-мерным кубом.

Для построения n-разрядного кода с выявлением ошибок нужно не больше половины от 2" возможных комбинаций разрядов. Выбор кодовых наборов проводится таким образом, чтобы при преобразовании одного допустимого кодового набора в другой допустимый кодовый набор по крайней мере два разряда имели противоположные значения.

Математические основы цифровой схемотехники

11

Рис. 1.1. Геометрическая интерпретация корректирующих кодов

Лекция

Коды с исправлением ошибок

Не только обнаружить, но и исправить ошибку можно с помощью кодов, ко­торые строятся следующим образом. Пусть есть m-значный двоичный код. Общее число комбинаций

N = 2^m.

Каждый из таких кодов отличается один от другого хотя бы одним знаком. Дополним код еще одним знаком, а число кодовых комбинаций оставим не­изменным, тогда

N = 2^m=1/2*2ⁿ

и можно так подобрать кодовые комбинации, что они будут отличаться дву­мя знаками. При этом используется только половина всех возможных комби­наций от 2ⁿ, вторая половина образует запрещенные комбинации: любое по­явление одиночной ошибки превращает ее в запрещенную и тем самым ошибка обнаруживается. Дополним теперь код таким количеством знаков, которое даст возможность двум кодовым комбинациям отличаться тремя знаками при неизменном числе N = 2^m. Такой код позволит не только обна­ружить, но и исправить одиночную ошибку. Действительно, если произошла одиночная ошибка в какой-то комбинации, то эта комбинация от других бу­дет отличаться на два знака, а от своей — на один, и ее легко исправить. Определим общее число дополнительных знаков, необходимых для выявления и исправления одиночных ошибок. Пусть из общего числа позиций п для пере­дачи информации используется фиксированное число позиций т. Другие пози­ции k= п — т используются как проверочные. Символы, которые ставятся на k проверочных позициях, определяются при кодировании проверкой на четность каждой k-ой группы информационных символов. Сигнал кодируется так, чтобы в результате любой из проверок выходило четное число. На приемном конце на некоторых позициях появляются единицы вместо нулей и нули вместо еди­ниц. При приеме также проводится проверка на четность.

Построим код, который разрешал бы обнаружить и исправить одиночную ошибку. Пусть принята кодовая комбинация с ошибкой или без нее. Сделаем в ней последовательно k проверок. После каждой проверки запишем 0, если результат свидетельствует об отсутствии ошибки на позициях, т. е. сумма единиц четная. Результат свидетельствует о наличии ошибки, если сумма единиц нечетная и тогда записывается 1. Запись справа налево полученной последовательности единиц и нулей дает двоичное число. Отсутствию ошиб­ки в принятой кодовой комбинации будет отвечать число, составленное из нулей. Проверочное число должно описывать (т + k + 1) событий. Следова­тельно, число k определяется на основе неравенства 2 >т + k + 1, и поскольку

2ⁿ п = т + k, то 2^m .п + 1

Это соотношение позволяет определить максимальное т при данном и или минимальное п для данного т. Соответствующие значения приведены в таблице 1

Определим позиции, которые надлежит проверить в любой из k проверок. Если ошибок нет, то на всех позициях, которые проверяются, будет 0, если в низшем разряде числа стоит 1, то это означает, что вследствие первой про­верки выявлена ошибка.

Таблица 1-

		Таблица 1.6.	Соотношения для корректирующих кодов
n	т	k	n	m	k
1	0	1	6	3	3
2	0	2	7	4	3
3	1	2	8	4	4
4	1	3	9	5	4
5	2	3	10	6	4

Будем при первой проверке проверять те номера позиций, двоичные пред­ставления которых имеют в первом разряде единицы, т. е.

1 = 0001; 3 = 0011; 5 = 0101; 7 = 0111; 9 = 1001 и т.д.

Таким образом, первая проверка охватывает позиции 1, 3, 5, 7, 9. Для второй проверки выберем такие позиции, двоичные представления которых имеют единицу во втором разряде — отвечающие числам 2, 3, 6, 7, 10. Для третьей проверки выберем позиции, двоичные представления которых имеют единицу в третьем разряде, т. е. имеем 4, 5, 6, 7, 12, 13, 14.

Такой выбор позиций, которые проверяются, дает возможность определить номер позиции, в которой возникла одиночная ошибка. Если возникла ошибка на одной из позиций первой проверки, то в проверочном числе в низшем (правом) разряде появится единица. Дальнейшую расшифровку проверочного числа дает вторая проверка: если среди всех позиций второй проверки ошибок нет, то появится ноль. Таким образом, любая одиночная ошибка на любой позиции может быть устранена проверками, которые дают проверочное число, равное номеру позиции, на которой возникла ошибка. Выбор для проверки позиций 1, 2, 4, 8 ... обеспечивает появление хотя бы одной из этих позиций в каждой проверке, и это позволяет независимо от знаков числа, которое передается, получить в каждой проверке четное число единиц.

Таким образом, основные принципы построения кодов Хемминга с исправ­лением ошибок состоят в следующем. К каждому набору из m информаци­онных разрядов присоединяется k разрядов p₁, p₂...p_k проверки на четность. Потом присваиваются десятеричные значения позиции любому с (m + k) разрядов кодового набора, начиная со значения 1 для старшего разряда и кончая значением (m +k) для младшего разряда. Проводится k проверок на четность числа единиц в выбранных разрядах каждого кодового набора. Ре­зультат проверки на четность записывается как 1 или 0 в зависимости от того, выявлена ошибка или нет. По результатам этих проверок строится двоичное число с_ь с₂, ...c_k равное десятеричному значению присвоенного местоположе­ния ошибочного разряда. При отсутствии ошибки записывается ноль. Это число называется номером позиции. Для определения контрольных разрядов независи­мо друг от друга через информационные разряды первые размещают на позици­ях 1, 2, ...2^k-1 Минимальное расстояние для кода Хемминга равняется трем. Корректирующую способность кода можно повышать и дальше: строя коды для выявления r-ой кратной и исправления 5-ой кратной ошибок. При этом бу­дет расти число дополнительных знаков и общая длина кодовой комбинации

(при неизменном N = 2^m ). Очевидно, что d = 1 + r + s, r>s.

14

Глава 1

Возможности разных кодов видны из табл. 1.7.

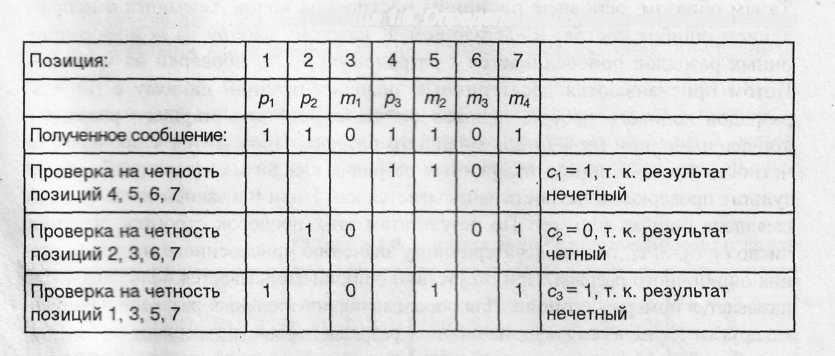
Таблица 1.7. Возможности корректирующих кодов

d	г	S	Возможности кода
1	0 .	0	Отличие одной комбинации от другой
2	1	0	Выявление одиночной ошибки
3	1	1	Выявление и исправление одиночной ошибки
	2	0	Выявление двукратной ошибки
4	2	1	Выявление двукратной и исправление одиночной ошибки
	3	0	Выявление трехразовой ошибки
5	2	2	Выявление и исправление двукратной ошибки
	3	1	Выявление трехразовой и исправление одиночной ошибок
	4	0	Выявление четырехразовой ошибки

Пусть, например, передана последовательность 1101001, но из-за ошибки в пятой позиции принята последовательность 1101101. Положение ошибки можно определить путем выполнения трех проверок на четность (табл. 1.8).

Таблица 1.8. Определение положения ошибки в коде

Таким образом, полученный номер позиции равен 101, что означает наличие ошибки в пятой позиции. Для ее исправления необходимо заменить пятый разряд его дополнением, после чего будем иметь правильное сообщение 1101001.

Глава 3

Методы минимизации булевых функций

3.1. Целые минимизации логических устройств

Логическую схему, которая реализует заданный алгоритм преобразования сигналов, можно синтезировать непосредственно по выражению, представ­ленному в виде СДНФ или СКНФ. Тем не менее, полученная при этом схема, как правило, не оптимальна с точки зрения ее практической реализации. По­этому исходную логическую функцию обычно минимизируют.

Целью минимизации логической функции является уменьшение стоимости ее технической реализации. Критерий, соответственно которому выполняется минимизация, далеко не однозначный и зависит как от типа задачи, так и >ровня развития технологии.

Основные требования к задаче синтеза: минимальное число элементарных конъюнкций или дизъюнкций в логической формуле и однородность исполь­зуемых операций. Кроме требований минимизации ставится ряд ограничений ■ условий на выбор элементной базы для синтезированного устройства.

3.2. Метод непосредственных преобразований

Непосредственное упрощение исходной логической функции, заданой в виде СДНФ, выполняется в следующем порядке [10]:

. Для каждой из возможных пар соседних конституент СДНФ применяется операция полного склеивания. При этом из них исключается по одной пе­ременной. Потом выполняется приведение подобных членов. Этот про-

46