Раздел I гидромеханические процессы и аппараты

Раздел 1. Гидромеханические процессы

И АППАРАТЫ 38ч., в т.ч. лаб. раб. и практ. занят 22ч.

Тема 1.1. Общие вопросы прикладной гидромеханики 12ч., в т.Ч. Лаб. Раб. И практ. Занят 8ч.

Студент должен:

знать:

• зависимость свойств жидкостей от давления, температуры;

• сущность гидростатического, абсолютного и избыточного давления;

• уравнения расхода и материального баланса потока;

• уравнение энергетического баланса;

• потери напора и давления при движении жидкости;

• порядок расчетов трубопроводов;

уметь:

• определять по справочнику свойства жидкостей в зависимости от условий;

• определять давление в назначенных точках систем;

• рассчитывать режим движения жидкостей;

• определять потери давления и напора;

• определять основные расходные характеристики, диаметр трубопровода;

• рассчитывать гидравлическое сопротивление зернистого слоя.

Реальные и идеальные жидкости. Физические свойства и параметры реальной жидкости. Гидростатика. Гидростатическое давление и его свойства. Гидродинамика. Уравнение материального баланса. Энергетический баланс потока. Уравнение Бернулли. Основные критерии гидродинамического подобия. Гидродинамические режимы вязкой жидкости. Гидродинамические сопротивления трубопроводов и аппаратов. Движение жидкости через неподвижные, пористые и зернистые слои. Гидродинамика псевдоожиженного слоя.

Общие вопросы прикладной гидромеханики

Гидромеханика – раздел механики сплошных сред, изучающий законы равновесия (гидростатика) и движения (гидродинамика) жидкостей и газов, а также механическое взаимодействие между жидкостью и твердыми телами (стенками), омываемыми ею. В отличие от твердых тел жидкости и газы обладают свойствами текучести, т. е. даже очень малые силовые воздействия вызывают их деформацию.

Прикладная гидромеханика, или гидравлика, - техническая наука, представляющая собой механику жидкости, в которой широко используются обоснованные допущения и предположения, упрощающие рассмотрение процессов. В гидравлике широко используют экспериментальные данные, которые позволяют ре­шать сравнительно сложные практические задачи механики жидкости.

С этой целью в гидромеханике вводится понятие идеальной жидкости, которая в отличие от реальной (вязкой) жидкости абсолютно несжимаема, т. е. не меняет плотность при изменении давления и температуры, а также не обладает внутренним трением между ее слоями (вязкостью).

В свою очередь реальные жидкости делятся на капельные (жидкости) и упругие (газы и пары), причем, если первые практически несжимаемы и обладают малым коэффициентом объемного расширения, объем последних значительно изменяется при изменении температуры и давления.

К основным физическим величинам, характеризующим Свой­ства рассматриваемых сред, относятся:

плотность (ρ, кг/м³), определяемая в случае однородного тела отношением

ρ=m/V,

где m - масса тела; V- его объем;

удельный вес (γ, Н/мз), определяемый для однородного тела отношением

γ= G/V,

где G – вес тела.

Поскольку вес тела и его масса связаны соотношением

G = mg,

где g – ускорение свободного падения (на поверхности Земли g = 9,81 м/с²), плотность тела является величиной постоянной, а удельный вес того же тела - величиной переменной в зависимости от значения ускорения свободного падения.

Плотность и удельный вес капельных жидкостей значительно больше, чем соответствующие характеристики упругих жидкостей (газов);

• давление (р, Н/м²), определяемое выражением

P = P/F

где Р – сила, действующая на поверхность F перпендикулярно к ней.

Поскольку упругие жидкости обладают сжимаемостью, их плотность в значительной степени зависит от давления и температуры. Связь между ними может быть определена уравнением состояния

где V – объем газа, м³; m – масса газа, кг; R = 8,31*103 Дж/(кмоль*град) – универсальная газовая постоянная; Т – температура, К; М – молекулярная масса газа, кг/кмоль.

Из уравнения (1.1) следует, что плотность упругих жидкостей определяется зависимостью

• вязкость молекулярная (физическая) – свойство реальной жидкости оказывать сопротивление движению в результате возникновения сил внутреннего трения.

При течении реальной жидкости скорость соседних слоев различается на величину dw. Таким образом, для перемещения одного слоя относительно другого необходимо приложить некоторую силу Т, которая, отнесенная к поверхности перемещаемых слоев F, позволяет получить характерный для рассматриваемой жидкости параметр, называемый напряжением внутреннего трения τ,

τ = Т/F.

Согласно закону Ньютона – Петрова

где dw/dn – градиент скорости, характеризующий изменение скорости по нормали между слоями.

Коэффициент пропорциональности (µ, Па*с) в уравнении (1.2) называется динамической вязкостью (иногда его называют коэф­фициентом вязкости, коэффициентом внутреннего трения).

Величину, равную отношению динамической вязкости к плот­ности среды, называют кинематической вязкостью (ν, м²/с)

Вязкость капельных жидкостей снижается с увеличением температуры, в отличии от вязкости газов, которая увеличивается с ее повышением;

• поверхностное натяжение (коэффициент поверхностного натяжения) (б, Н/м) определяется как отношение силы Р, действующей на участок контура поверхности жидкости, к длине l этого участка:

и определяет формирование поверхности на границе раздела жидкость – газ (пар) или жидкость – жидкость (несмешиваемые друг с другом).

Значения величин плотностей, вязкостей и поверхностного

натяжения для различных сред и условий можно найти в специ­альной справочной литературе.

Гидростатика – раздел гидромеханики, в котором изучается состояние жидкостей, находящихся в относительном покое или условиях равновесия, когда частицы и слои, составляющие их, не перемещаются друг относительно друга. Поскольку при этом внутренние силы (трения) отсутствуют, а рассматриваются только внешние силы (тяжести, давления), жидкость близка к идеальной.

Давление жидкости Р на единицу поверхности F называется гидростатическим давлением (р, Н/м²) и определяется соотношением

Однако истинное гидростатическое давление – это давление в точке, которое определяется как

К основным свойствам гидростатического давления можно отнести следующие:

• гидростатическое давление определяется весом столба жидкости высотой h над рассматриваемым участком:

Если давление над жидкостью равно ро, то

Р = р_о + hρg;

• гидростатическое давление всегда направлено от жидкости к воспринимающей поверхности по перпендикуляру;

• величина гидростатического давления на одном уровне жидкости одинакова по всем направлениям.

Гидродинамика – раздел гидромехани ки, в котором рассматриваются задачи, связанные с движением жидкости под действием приложенных к ней внешних сил – разности давлений, создаваемой с помощью н агнетательного оборудования (насосов или компрессоров), либо вследствие разности уровней или плотностей жидкостей.

При рассмотрении течения жидкости по запол ненному трубопроводу различают:

• линейную скорость w – путь, пройденный количеством жидкости в единицу времени.

В связи с тем, что скорость отдельных слоев жидкости неодинакова, чаще рассматривают среднюю скорость потока (w, м/с)

w = V/F (1.3)

где V – объемный расход потока; F – площадь поперечного сечения трубопровода;

• объемный расход потока (V, м³/с), определяемый по уравнению, обратному (1.3),

V = wF;

• массовую скорость (W, кг/(м²*с)), определяемую как количество жидкости, перемещенное через единицу поперечного сечения в единицу времени,

W = G/F = wρ, (1.4)

где G = Wρ — массовый расход жидкости.

В случае установившегося (стационарного) движения, когда все параметры, характеризующие состояние системы в каждом сечении (скорость, расход, температура, плотность и др.), не меняются во времени, при переходе от сечения F₁ к сечению F₂ скорости жидкости w₁ и w₂ будут различны, однако по закону сохранения вещества массовый расход жидкости, проходящей через каж­дое сечение, должен быть неизменен.

Таким образом, в соответствии с уравнением (1.4)

G = F₁*w₁*ρ₁ = F₂*w₂*ρ₂ = const. (1.5)

Считая жидкость несжимаемой (ρ₁ = ρ₂) уравнение (1.5) можно записать

V= F₁*w₁ = F₂*w₂ = const. (1.6)

Уравнения (1.5) и (1.6) называются уравнениями неразрывности потока и представляют собой материальный баланс потока жидкости.

Любая жидкость, находящаяся в состоянии относительного покоя или движения, обладает запасом энергии, равным сумме внутренней, потенциальной и кинетической энергии.

Внутренняя энергия U представляет собой суммарную энергию молекул жидкости, величина которой определяется многими параметрами – в частности температурой, с увеличением которой она возрастает.

Потенциальная энергия является суммой потенциальной энергии давления рV и потенциальной энергии положения mgz. Последняя определяется высотой центра тяжести г рассматриваемого объема жидкости над некоторой произвольно выбранной горизонтальной плоскостью (плоскостью сравнения).

Кинетическая энергия объема жидкости массой т, движущейся со скоростью w, определяется выражением m*w²/2.

Таким образом, полная энергия жидкости Е, равная сумме перечисленных энергий, составит

Обозначив сумму внутренней и потенциальной энергии давления

называемой энтальпией (теплосодержанием) потока, запишем уравнение (1.7) как

Удельная энергия е, приходящаяся на 1 кг жидкости, может быть представлена делением уравнений (1.7) и (1.8) на m:

где u – внутренняя энергия 1 кг жидкости; v -объем, занимаемый 1 кг жидкости; i - энтальпия 1 кг жидкости.

В случае установившегося (стационарного) движения Жидкости по трубопроводу переменного сечения (рис. 1.1) без дополнительного подвода или отвода энергии ее удельная энергия по закону сохранения изменяться не будет. Поэтому при перемещении жидкости от некоторого сечения 1 – 1 до сечения 2 – 2, удельная энергия жидкости в них также не меняется:

Поскольку v = 1/ρ, уравнение (1.9) можно представить в виде

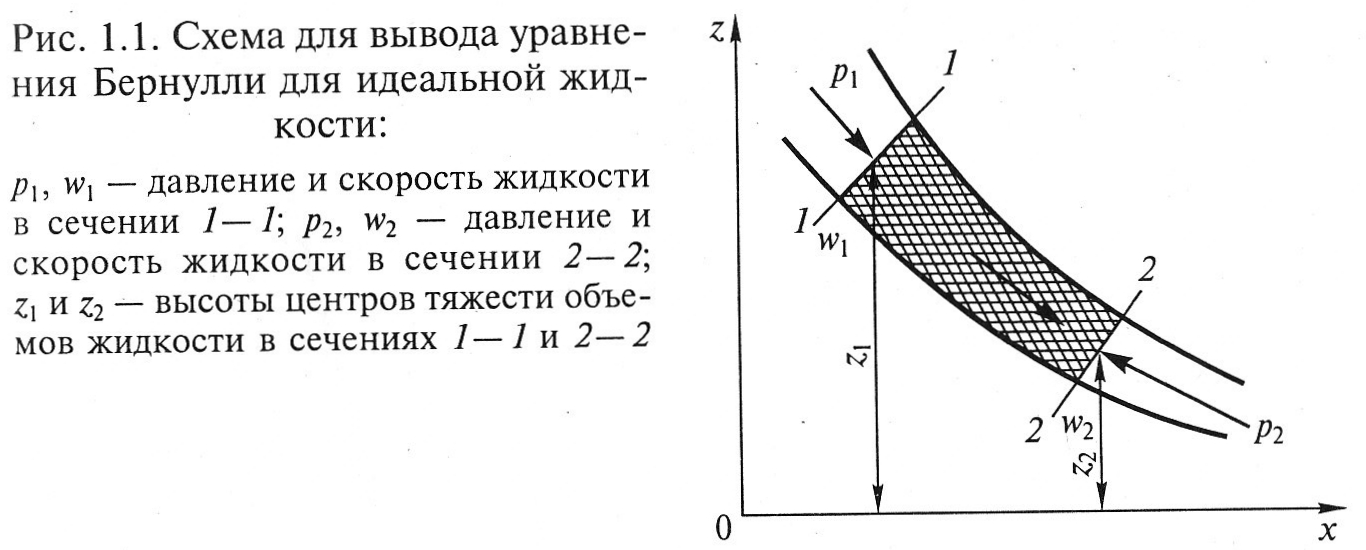
Учитывая, что для идеальной жидкости ρ₁ = ρ₂ = ρ (условие несжимаемости), u₁= u₂ (отсутствие внутреннего трения), уравнение (1.10) запишем как

Данное уравнение, записанное в общем виде

называется уравнением Бернулли для идеальной жидкости, а сумма в левой части – гидродинамическим напором.

При записи уравнения Бернулли для реальной жидкости необходимо учитывать изменение внутренней энергии системы между сечениями 1 – 1 и 2 – 2 введением в правую часть уравнения (1.11) слагаемого (u₁- u₂)/g:

Основные критерии гидродинамического подобия

На элемент движущейся среды в потоке действуют силы тяжести, давления, а также вязкого трения (сопротивления). Сумма этих сил в соответствии с принципом Д'Аламбера равна силе инерции

Рассмотрим частные случаи существенного преобладания одной из сил над другими с позиций теории подобия.

В случае преобладания силы тяжести mg, когда остальными силами можно пренебречь, баланс сил может быть записан в виде дифференциального уравнения или в соответствии с правилами применения теории подобия

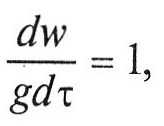
где m - масса жидкости; g - ускорение свободного падения.

Убрав знаки дифференцирования и заменив τ = l/w, получим критерий Фруда Fr = w²/(gl), где w - скорость; l – определяющий линейный размер.

При преобладании сил давления Δр/l² баланс сил может быть записан дифференциальным уравнением

где Δр – перепад давлений; l – определяющий линейный размер.

Убрав знаки дифференцирования и заменив τ = l/w и m = l³*ρ, получим критерий Эйлера Еu = Δр/(ρw²), где ρ - плотность среды.

При преобладании сил вязкости записан как баланс сил может быть

Убрав знаки дифференцирования и заменив τ = l/w и m = l³*ρ, получим критерий Рейнольдса

где µ, v - динамическая и кинематическая вязкости среды соответственно.

Таким образом, критерий Фруда характеризует подобие процессов, протекающих под действием силы тяжести, и выражает соотношение сил инерции и сил тяжести. Критерий Эйлера характеризует соотношение сил давления и сил инерции, а критерий Рейнольдса – сил инерции и сил трения.

При описании неустановившегося движения в ряде случаев используют критерий гомохронности

часто называемый в зарубежной литературе критерием Струхаля (Str).

Кроме этого в гидромеханике часто используют ряд других критериев:

• критерий Галилея, характеризующий соотношение сил моле­кулярного трения и сил тяжести,

• критерий Архимеда, характеризующий соотношение сил Тя­жести, подъемной силы и сил трения,

где ρ_ч – плотность частиц.

Гидродинамические режимы вязкой жидкости

В зависимости от характера движения различают ламинарный и турбулентный режимы течения жидкостей. Установлено, что численная характеристика режима течения может быть осуществлена с использованием критерия Рейнольдса , где в качестве характерного линейного размера используется диаметр трубопровода d.

Ламинарный режим (от лат. lamina – пластинка, полоска) наблюдается при малых скоростях или высокой вязкости жидкости.

Характерной особенностью такого течения является движение слоев жидкости параллельными струйками, не смешивающимися друг с другом, причем скорость каждой из них постоянна и направлена вдоль общего течения. Ламинарный режим течения жидкостей наблюдается в трубах при значениях Re < 2300.

При турбулентном режиме (от лат. turbulentus – бурный, беспорядочный) движение в жидкости носит хаотический характер, слои постоянно перемешиваются. Частицы перемещаются с различными скоростями по неопределенно искривленным траекториям, в то время как вся масса жидкости движется в одном направлении. Устойчивый турбулентный режим течения в трубах наблюдается при значениях Re > 10000.

В пределах значений Re от 2300 до 10000 турбулентное движение является неустойчивым (переходная область).

При анализе движения жидкости по трубопроводам сложной конфигурации в критерии Re в качестве характерного линейного размера используют эквивалентный диаметр

где F — площадь сечения канала; П — периметр канала, смочен­ный жидкостью.

Гидравлическое сопротивление трубопроводов

При движении реальной жидкости по трубопроводам происходит потеря напора или давления, о6условленНая сопротивлением трения и местными сопротивлениями, возникающими при изменении направления или скорости потока (сужения, расширения, вентили, изгибы и т.д.).

Потери на трение имеют место по всей длине трубопровода и определяются по уравнению Вейсбаха-Дарси

где w_ср – средняя скорость течения жидкости по трубопроводу; λ – коэффициент гидравлического сопротивления, зависящий от режима течения потока. При турбулентном движении λ зависит от шероховатости стенок трубы, которая оценивается величиной относительной шероховатости

где Δ – средняя высота выступов на внутренней поверхности трубы диаметром d.

Исследования сопротивления трения шероховатых труб, выполненные Никурадзе (рис. 1.2), показали, что наблюдаются три характерные области изменения а, в зависимости от режима движения и шероховатости труб:

• ламинарный режим, при котором λ = f(Re) и λ = 64/Re;

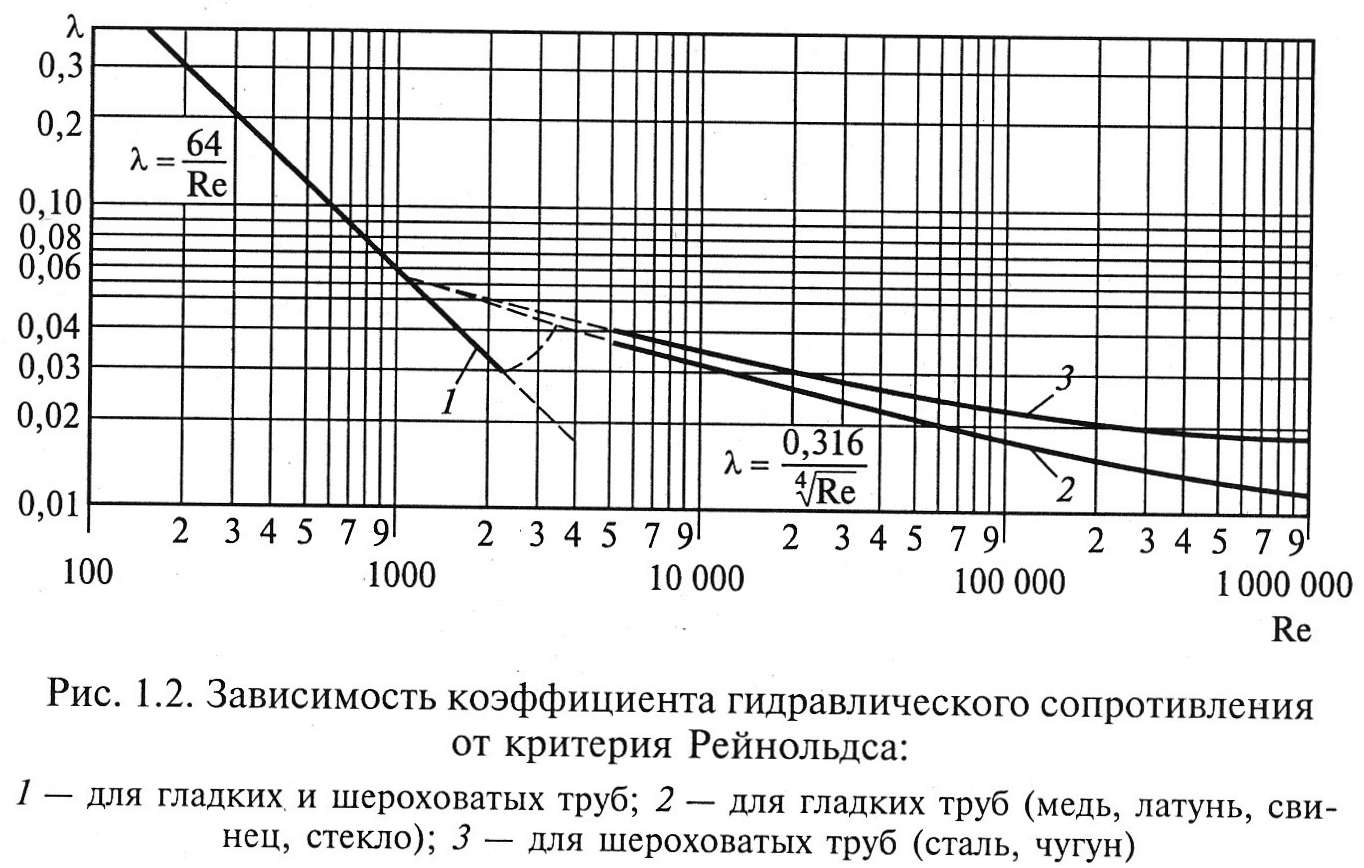
турбулентный режим, где λ=f(Re, ε) для гидравлически гладких труб

λ = 0,316/Re0,25;

автомодельная область по отношению к критерию Re (т. е. не зависящая от значения Re) = ƒ(ε).

Потери давления в местных сопротивлениях Δp_м.с выражают как

Δр_м.с = ζρw_ср²/2,

где – ζ коэффициент местного сопротивления.

Движение жидкости через неподвижные, пористые и зернистые слои

Многие гидромеханические процессы связаны с движением капельных жидкостей или газов через неподвижные слои твердых материалов, состоящих из отдельных элементов.

К основным характеристикам такого движения относятся:

• гидравлическое сопротивление слоя Δр_сл которое можно рас­считать по уравнению, сходному с выражением (1.13),

где l_к – длина каналов в слое; w – средняя (истинная) скорость потока в канале; d_экв – эквивалентный диаметр каналов; λ = f(Rе_сл) – коэффициент гидравлического сопротивления слоя;

• порозность, или объемная доля пор в слое,

где V – объем пористого слоя; V_тв – объем твердой фазы в слое;

• истинная и фиктивная скорости – для удобства расчета в уравнении (1.14) часто используется не w (истинная скорость в каналах слоя), а w_Ф – фиктивная скорость потока, отнесенная к сечению аппарата, в котором размещен слой.

Связь между средней и фиктивной скоростью определяется уравнением неразрывности

wf_k = w_Фf,

где f_k, f сечения каналов и аппарата, соотношение между кото­рыми легко определить как

откуда

где Н - высота зернистого слоя;

• эквивалентный диаметр каналов в зернистом слое

где а = S_K/V – удельная поверхность частиц в слое, величину которой для слоя с частицами одинакового размера можно рассчитать по зависимости

где ψ =f_Ш/f -фактор формы, представляющий отношение поверхности шарообразной частицы f_Ш, имеющей тот же объем, что и рассматриваемая частица с поверхностью f; d – диаметр частиц в слое;

• длина каналов l_К с учетом коэффициента извилистости каналов k может быть записана как

где Н – высота зернистого слоя.

При подстановке зависимостей (1.15)-(1.18) в уравнение (1.14) получим

Одновременно коэффициент гидравлического сопротивления может быть рассчитан для всех режимов течения по эмпиричес­кой зависимости

Гидродинамика псевдоожиженного слоя

При пропускании потока газа или жидкости через слой зернистого материала со скоростью w_Ф < w_кp1 слой остается неподвижным, газ (жидкость) фильтруется через него, не нарушая общей структуры. Сопротивление слоя при этом возрастает пропорционально увеличению скорости потока.

При достижении скорости w_кp1 вес зернистого материала в слое уравновешивается силой трения потока о поверхности частиц, которые переходят во взвешенное состояние и впоследствии приобретают возможность перемещения друг относительно друга. Скорость w_кp1 называется первой критической скоростью или скоростью начала псевдоожижения, а слой, находящийся в таком состоянии, называется псевдоожиженным, т. е. обладает свойствами, близкими к жидкости. Слой в этом случае приобретает текучесть, принимает форму аппарата, в котором находится, характеризуется вязкостью, на погруженные в него тела действует сила Архимеда. При дальнейшем увеличении скорости газа (жидкости) слой расширяется, его порозность и интенсивность движения частиц увеличиваются. Поскольку вес слоя при этом не изменяется, его сопротивление потоку остается неизменным.

При достижении w_Ф = w_кp2 начинается разрушение однородности слоя и унос из него частиц. Скорость w_кp2 называется второй критической скоростью или скоростью уноса.

Широкое использование аппаратов с псевдоожиженным слоем в промышленном производстве объясняется такими его свойствами, как выравнивание полей температур и концентраций компонентов в объеме технологических аппаратов; максимальное развитие поверхности взаимодействия между ожижающим агентом и зернистыми материалами (поверхности фазового контакта); возможность транспортировки зернистых материалов в псевдоожиженном состоянии; незначительное гидравлическое сопротивление слоя во всем диапазоне скоростей псевдоожижения; простота конструктивного оформления технологических аппаратов с псевдоожиженным слоем и возможность автоматизации их работы.

Наряду с перечисленными достоинствами псевдоожиженному слою свойственны некоторые недостатки: уменьшение движущей силы процесса, вызванное выравниванием концентрационных и температурных полей; возможность проскока значительных количеств газа без достаточного контакта с твердым материалом; возможность эрозионного изнашивания при трении твердых частиц о стенки аппаратов; возникновение электростатических зарядов при трении диэлектрических частиц друг о друга; необходимость дополнительной установки мощных газоочистных устройств и т. д.

Основной характеристикой псевдоожиженного слоя является кривая псевдоожижения, представляющая собой зависимость между его гидравлическим сопротивлением и фиктивной скоростью ожижающего агента (рис. 1.3).

Кривая, показанная на рис. 1.3, а, называется кривой идеального псевдоожижения монодисперсного слоя твердых частиц, т. е. частиц одинакового размера. В зависимости от значений скорости w_Ф на ней различают области фильтрации ожижающего агента через неподвижный слой (0 < w_Ф < w_кp1), псевдоожижения (w_кp1 < w_Ф < w_кp2), Уноса (w_Ф > w_кp2).

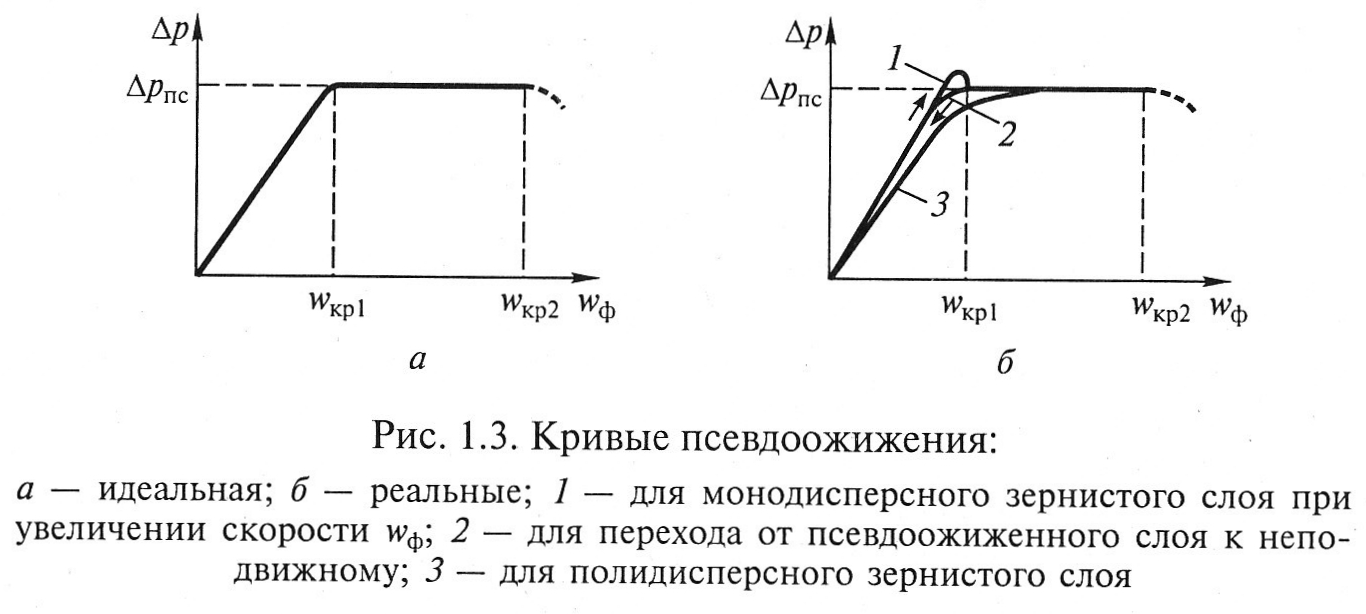
Реальная кривая псевдоожижения (рис. 1.3, б) монодисперсного зернистого слоя (слоя с частицами одинакового размера) отличается от идеальной тем, что в момент перехода в псевдоожиженное состояние имеет место скачок давления (кривая 1), что вызвано необходимостью преодоления сил сцепления частиц. Величина этого пика зависит от формы и состояния поверхности твердых частиц, а также плотности их упаковки. В случае снижения скорости w_Ф переход от псевдоожиженного слоя к неподвижному происходит по кривой 2, на которой пик отсутствует.

В случае псевдоожижения полидисперсного зернистого слоя (слоя с частицами разного размера) четко выраженная скорость w_{КР 1} отсутствует (кривая 3), так как переход слоя в псевдоожиженное состояние происходит постепенно (пофракционно) – от мелких к крупным частицам.

Скорость начала псевдоожижения w_KP1 может быть определена исходя из того, что она принадлежит как областям фильтрования, так и псевдоожижения.

В первом случае перепад давлений может быть определен по зависимости (1.19), записанной для данных условий в виде

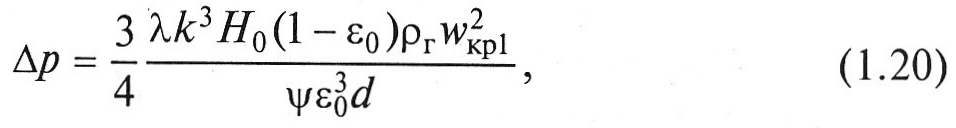
где Н₀, ε₀ - высота и порозность неподвижного слоя соответственно; ρ_г – плотность газа (псевдоожижающего агента).

Во втором случае перепад давлений может быть определен исходя из того, что гидравлическое сопротивление слоя равно весу слоя G_сл за вычетом действующей на него силы Архимеда G_А и отнесено к площади сечения аппарата f

или

Поскольку Δp = Δр_пс, приравняв зависимости (1.20) и (1.21), получим скорость начала псевдоожижения для частиц диаметром d рассматриваемой фракции (ψ = 1)

При ламинарном режиме течения ожижающего агента между частицами слоя (Re < 35)

λ= А/Re,

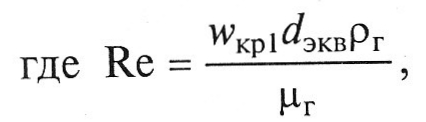
или, учитывая зависимости (1.15) - (1.17),

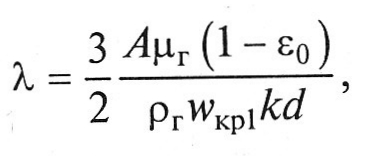
уравнение (1.22) перепишется как

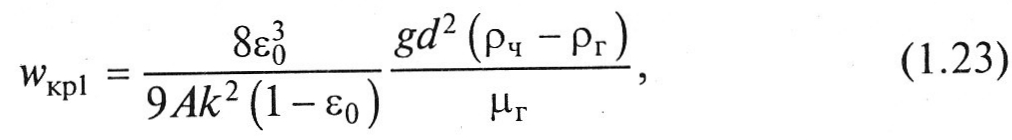
где ε₀ – порозность неподвижного слоя; g – ускорение свободного падения; А – коэффициент пропорциональности; k – коэффициент извилистости каналов.

Обозначив первый сомножитель как В и умножив правую и левую части уравнения (1.23) на комплекс получим

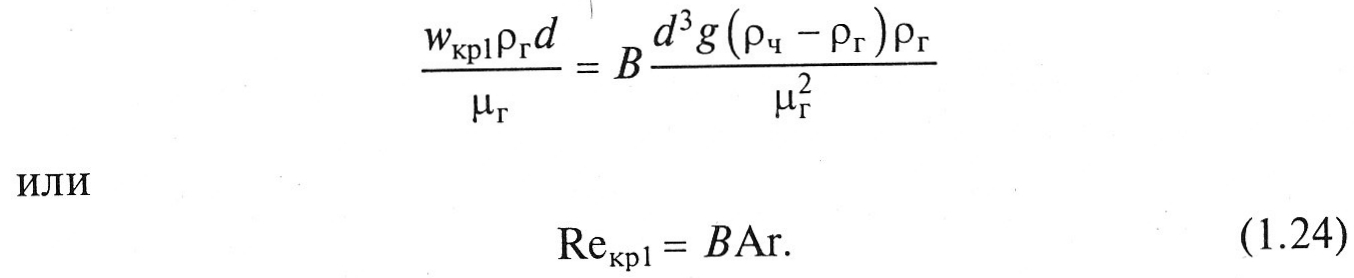
Уравнение (1.24) показывает возможность экспериментального определения скорости начала псевдоожижения в соответствии с правилами теории подобия через критерии Рейнольдса и Архимеда.

Контрольные вопросы

1. Что является предметом изучения гидромеханики?

2. Какими основными свойствами и параметрами характеризуется реальная жидкость?

3. Какими видами энергии обладают покоящиеся и движущиеся жидкости?

4. Какие критерии относятся к критериям гидродинамического подобия и каков их физический смысл?

5. Какие гидродинамические режимы течения вязкой жидкости различают?

6. Как определяется гидравлическое сопротивление трубопровода?

7. Какими параметрами характеризуется движение жидкости через неподвижные, пористые и зернистые слои?

8. Что характеризует кривая псевдоожижения?