9. Общая схема методов 2-го порядка. Метод Ньютона

Рассмотрим задачу:

(1)

В методах 2-го порядка на -ой итерации по известному приближению решается задача

(9)

– квадратичная аппроксимация. Если окрестность строится с помощью линейных ограничений, то (9) – задача квадратичного программирования, её решение – .

Различные способы задания окрестности задают различные методы. Будем решать (9) в 2 этапа:

I этап: , . Тогда придём к задаче:

, (10)

Решение этой задачи принимается за – направление итерации. Шаг выбирается одним из 3-х способов (из 3.3)

Пример. Пусть в задаче (1) выполняется условие

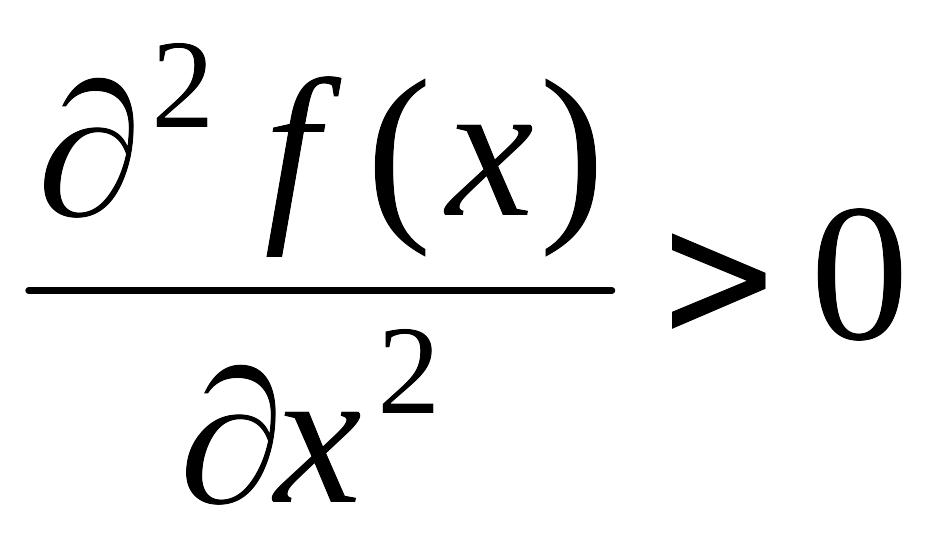(11)

то есть функция является строго выпуклой.

Замечание. Условие (11) может выполняться в некоторой окрестности решения задачи, тогда и функция строго выпукла . Задача (10) имеет решение, даже если положить и будет находиться в стационарной точке .

Положим в (10) и составим уравнение стационарности

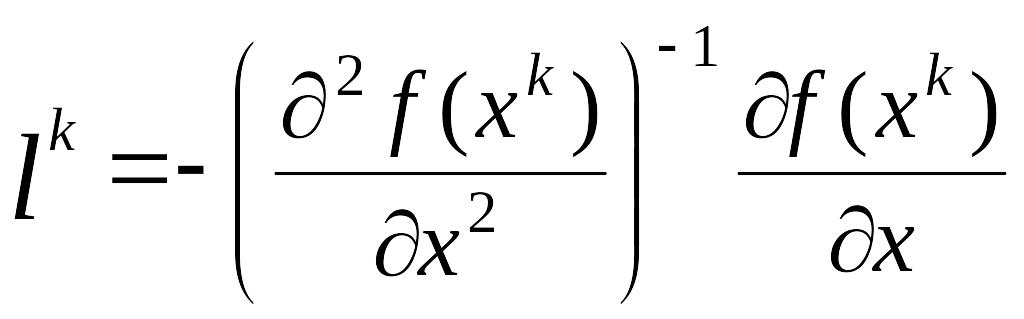(12)

Направление итерации, которое выбирается по формуле (12) называется направлением Ньютона, а методы, основанные на таком либо подобном направлении, называется ньютоновскими. В частности. Если положить , то получим классический метод Ньютона.

Геометрическая интерпретация направлений Ньютона: в к линии уровня строим касательный эллипс: . Направление Ньютона ведёт в центр эллипса (матрица 2-го порядка (12) как бы поворачивает антиградиент в сторону оптимального плана и нормализует его длину (формирует шаг)). Поэтому методы 2-го порядка более точные и быстрее сходятся.

12.Другие методы. О выборе метода

Для задачи (1) популярны методы многомерного поиска. Самый простой из них метод покоординатного спуска: на первой итерации в качестве направления выбирается 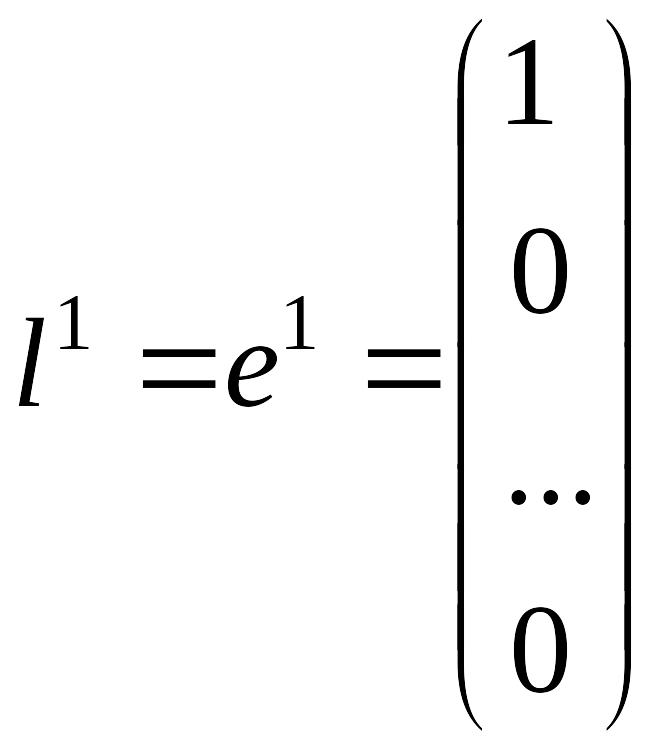, затем подбирается шаг с помощью решения задачи:

(13)

Замечание. В этом методе шаг может быть и отрицательный. Затем полагаем . На 2-ой итерации в качестве направления снова решается задача (13), находится шаг и строится , и так далее. На -ой итерации выбирается 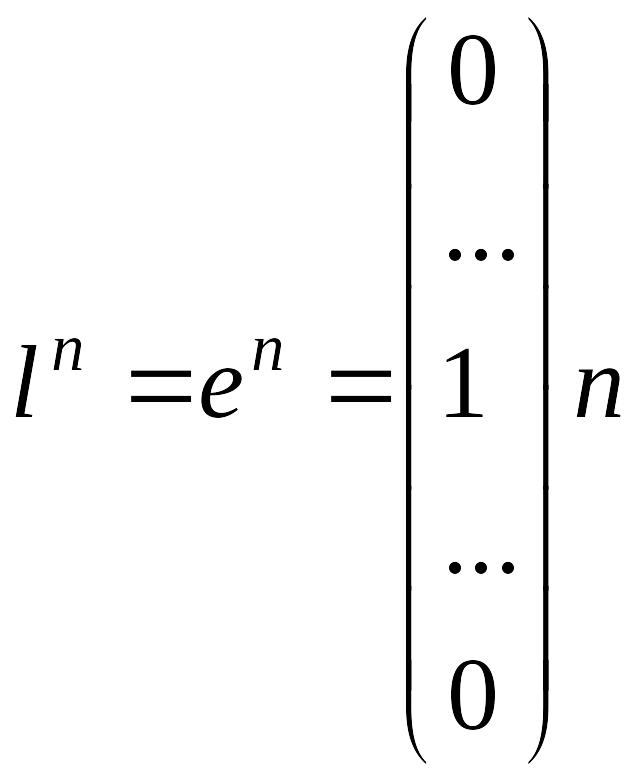решается задача (13) и получаем . Задача (13) решается методом последовательного подбора .

Первые итераций метода дают его полный цикл, если нас не удовлетворяет, то можно совершить ещё один цикл. В методе покоординатного спуска на каждой итерации решается одномерная задача минимизации (13) (можно использовать метод золотого сечения, Фибоначчи) и на каждом шаге улучшается лишь одна компонента плана.

Метод случайного поиска

В этом методе на -ой итерации по известному приближению в качестве выбирается некоторый случайный вектор единичной длины, . При этом используются механизмы теории вероятности (датчик случайных чисел). После того, как направление выбрано, проверяется, является ли оно подходящим. Если выполняется , для некоторого малого, то выбирается в качестве направлений итерации и осуществляется итерация, шаг выбирают по 3-ему способу. Если , то шаг изменяется на противоположный либо выбирается по-новому.

Замечание. Не всегда противоположное направление оказывается подходящим. (Если в качестве случайного направления выбрано касательное, то и противоположное не будет подходящим.)

Один из самых популярных методов 1-го порядка, который по сходимости близок к методу 2-го порядка – метод сопряжённого градиента.

При выборе метода для решения конкретной задачи надо учитывать всю информацию, тип целевой функции, её гладкость, форму поверхности уровня, кривизну и так далее.

Общая рекомендация: первые итерации лучше проводить грубыми методами (метод поиска), затем переходить к методу 1-го порядка, а затем в малых окрестностях решения можно использовать метод Ньютона (так как там обычно выполняется неравенство (12)).

10. МЕТОДЫ УСЛОВНОЙ МИНИМИЗАЦИИ. Случай линейных ограничений

Пусть дана задача:

(1)

Пусть требуется решить задачу:

(2)

где – множество простой структуры, которое задаётся с помощью ограничений на одну переменную вида .

В методах 1-го порядка на -ой итерации по известному решается задача

(3)

Как правило, окрестность в (3) формируется с помощью линейных ограничений. Поэтому задача (3) представляет из себя задачу линейного программирования, её решение принимается за .

Если в задаче (3) вначале искать направление итерации и положить , то в результате придём к задаче

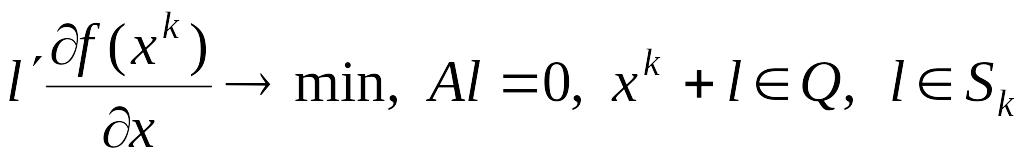(4)

Решение этой задачи принимается за . Задача (4), как правило, линейная задача. После определения направления итерации шаг выбирают одним из описанных 3-х способов.

Пример 1. Положим в (4), тогда получим задачу:

(5)

Решение этой задачи называется направлением условного градиента. Это направление даёт наибольшую проекцию на антиградиент и не выводит за пределы .

Пример 2. Положим , тогда получим задачу:

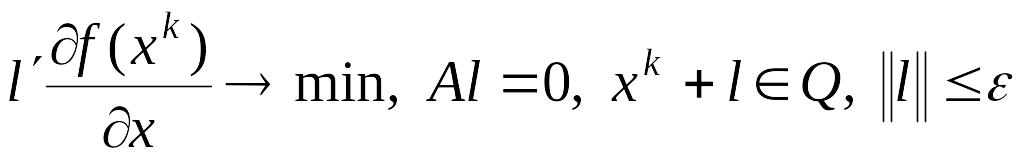(6)

а) . В этом случае совпадает по направлению с антиградиентом и имеет длину , (то есть в этом случае используется классический градиентный метод).

б) , значит, антиградиент проектируется на и имеет длину .

Если в (3) вместо использовать , то для задачи (2) получаем метод Ньютона.