6.Методы минимизации унимодальных функций. Метод Фибоначчи
Методы двухточечного поиска
Методы основаны на следующем свойстве унимодальных функций: знание функции в 2-х внутренних различных точках [ ] позволяют уменьшить интервал локализации точки минимума.
Пусть
даны
,
тогда если:
1
,
то
2
,
то
3
,
то
Поскольку 3-е условие на практике не встречается, то его для определённости включают в 1-ое условие.
В 2-х
точечных методах на нулевой итерации
полагаем
где
.
В этом
случае
лежат симметрично (равноудалено от
концов отрезка [
]).
Метод определяет
.
Используя основное свойство, уменьшаем отрезок локализации:
1 если
то полагаем
2 если
то
Переходим к первой итерации.
Опишем
-ую
итерацию: пусть дан отрезок
,
симметричные точки
тогда возможны 2 случая:
1 если
то
2 если
то
.
И так далее.
Если
то
задача локализации решена. В противном
случае переходим к
-ой
итерации.
Двухточечные методы позволяют значительно сокращать объём перебираемых планов, в них на 1-ой итерации функция вычисляется в 2-х точках, а на последующих итерациях в одной дополнительной точке.
Метод Фибоначчи
Этот метод наилучший из 2-х точечных методов в том смысле, что даёт минимальное количество точек перебора.
Задача: пусть на [ ] позволяется вычислить значение целевой функции не более чем в точках. Требуется так их разместить, чтобы в результате получить интервал локализации наименьшей длины. Эту задачу решает метод Фибоначчи.
Введём числа Фибоначчи:
Существуют
специальные таблицы чисел Фибоначчи,
где
.
В методе Фибоначчи на нулевой итерации
полагают
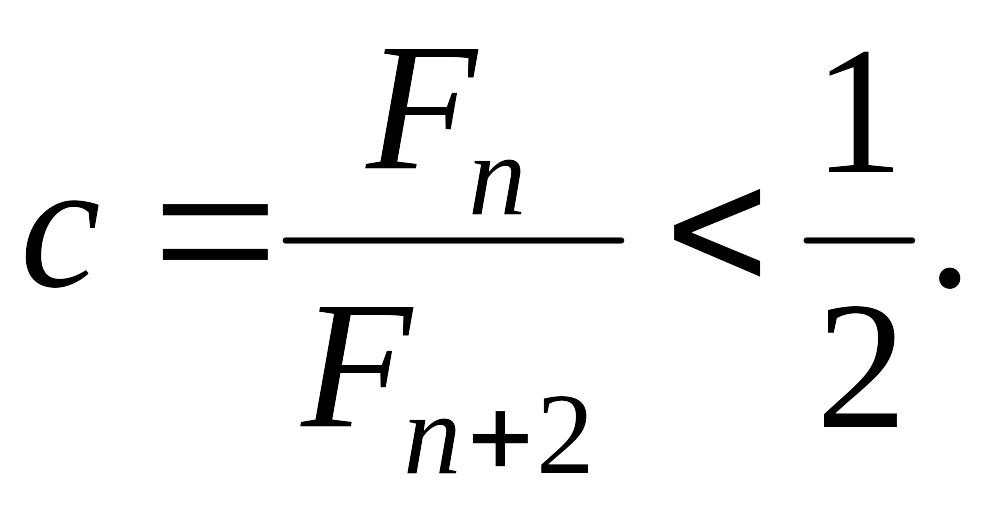
В дальнейшем используется общая схема двухточечных методов.
7.Методы минимизации унимодальных функций. Метод золотого сечения
Методы двухточечного поиска
Методы основаны на следующем свойстве унимодальных функций: знание функции в 2-х внутренних различных точках [ ] позволяют уменьшить интервал локализации точки минимума.
Пусть даны , тогда если:
1 , то 2 , то
3 , то
Поскольку 3-е условие на практике не встречается, то его для определённости включают в 1-ое условие.
В 2-х точечных методах на нулевой итерации полагаем где .
В этом случае лежат симметрично (равноудалено от концов отрезка [ ]). Метод определяет .
Используя основное свойство, уменьшаем отрезок локализации:
1 если то полагаем
2 если то
Переходим к первой итерации.
Опишем -ую итерацию: пусть дан отрезок , симметричные точки тогда возможны 2 случая:
1 если то
2 если то .
И так далее.
Если то задача локализации решена. В противном случае переходим к -ой итерации.
Двухточечные методы позволяют значительно сокращать объём перебираемых планов, в них на 1-ой итерации функция вычисляется в 2-х точках, а на последующих итерациях в одной дополнительной точке.
Метод золотого сечения
Определение.
Говорят, что точка
осуществляет
золотое сечение
[
]
на две неравные части. Если длина меньшего
отрезка так относится к длине большего
отрезка, как длина большего отрезка
относится к длине [
],
то есть если выполняется:
Найдём
расположение
,
для этого подставим
и найдём значение
:
;
,
,
В методе золотого сечения на нулевой итерации каждая из точек осуществляет золотое сечение [ ] (с разных сторон), в дальнейшем применяется общая схема двух точечных методов.