47. Модель прогнозирования отраслевых цен в системе моб

Базовая прогнозная модель нах примен при оценке разл эл-ов стоим-ой стр-ры пр-ва. В рамках данной модели б. полагать, что инфляц процесс хар-ся кол-но индексами среднеотрасл-ых цен р_i . Через q_i обозн индекс измен добавл ст-ти, обуслов-го влиянием ценового ф-ра при условиинеизмен реальн объемов пр-ва и стр-ры межотраслевого обмена. С 1м и 3м квадрантом получим след табл:

Отрасли-произ-ли	Отрасли-потреб
1	X11*p1	X12*p1	X13*p1
2	X21*p2	X22*p2	X23*p2
3	X31*p3	X32*p3	X33*p3
	∑хi1* pi	∑хi2* pi	∑хi3* pi
	Z1*p1	Z2*p2	Z3*p3
Вал.выпуск	X1*p1	X2*p2	X3*p3

Базовая прогнозн модель для оценки последствия инфляций запис в след виде:

х11р1+х21р2+х31р3+z1q1=x1p1

x12p1+x22p2+x32p3+z2p2=x2p2 (1)

x13p1+x23p2+x33p3+z3p3=x3p3

Если в рав-ве (1) замен отраслевые поставки. Ур-ие (1) примет след вид: x_ij=a_ijX_j , а11Х1р1+а21Х1р2+а31Х1р3+z1q1=X1P1 (2). Рав-во (2) кажд из ур-ий делят на соотв объем валового выпуска, тогда обознач ч-з _I отнош z_i /x_i : _I = z_i /x_i (3), т.е. отнош добавл ст-ти к валов выпуску и наз его нормой добавл ст-ти, соотн (2) мы запишем в матричн ф-ме: P=А^ТР+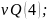 P= ; = ; Q= [q1, q2, q3]. А^Т – транспонир матр прямых материал затр мы получим вектор с, он м.б. опред из рав-ва:

р= (Е- А^Т)^-1 Q (5).

48. Понятие производственной функции (пф) одной и нескольких переменных

ПФ – ф-ция, выраж. Величину объема выпуска пр-ции в зав-ти от объемов затрач ресурсов. В самом общем виде ф-ция имеет вид: у=f(x) (1). x=(х₁, х₂,…,х_n) – вектор ресурсов.

у≥0, х_j≥0, j=1, n. Для связи вектора х д. ? вектор пар-ров: а=(а₁, а₂,…,а_n) – вектор пар-ров.

y=f(a,x) (1.1). Смысл. понятия ПФ завис от масштаба обл эк-ки. В микроэ-ке счит, что это макс возмож выпуск пр-ции при зад ресурсах. В макроэк производ ф-ия отраж стат устойчив связь м-ду затратами ресурсов и выпуском пр-ции для сущ сист форм собств-ти и управл. Самой простейшей ф-ей явл-ся

у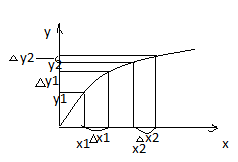 =а₀Х^а1 (2), где х – затрачив ресурс, у – объем выпуск пр-ции. Вследствие закона убывающей эф-ти 0<a₁<1; а₀>0.

По з-ну убывающ эф-ти справедливо:

x₂ >х₁

∆x₁=∆x₂

∆y₂<∆y₁

Показатели производ ф-ции м измер-ся натур ед-ми или стоимост, т.к. эти ф-ции явл-ся малыми (макро)эк-ми моделями, в осн использ стоимост показ-ли. Для перемен произв ф-ях использ след обознач:

У – эндогенные перемен совокуп пр-т, объем пром. пр-ва в неизменных ценах.

Экзогенные: К-объем использ капит, L – кол-во ед-ц живого труда.

Если К и L рассм за год и не вкл в себя ф-р врем, то модель наз стат-ой. Если время выступ в кач-ве самост перемен, то в модель ввод ф-р, учит влияние НТП, то такая модель динамическая.