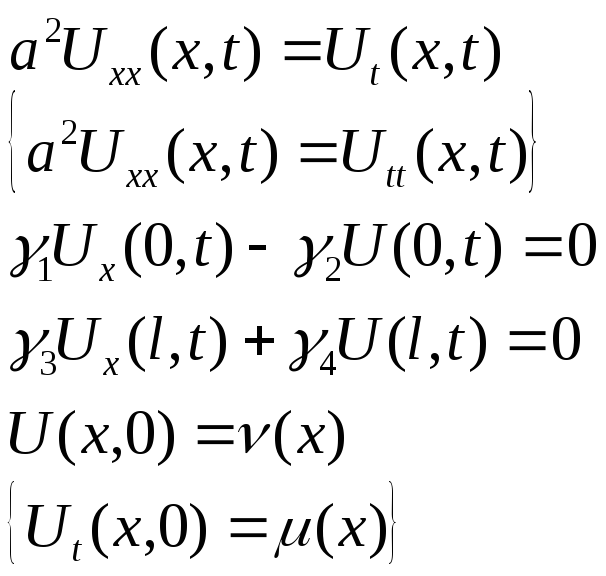как научиться решать урматы за 1 день до зачета!!! / шпоры / решения уравнений матфизики!

Однородные уравнение и краевые условия

Уравнение и краевые условия однородны

начальные условия могут быть произвольны

Метод Фурье: Ищем U(x,t) в виде:

Для Φ(x) получаем задачу Штурмана-Лиувиля (метод разделения переменных)

, С_n, D_n находим из начального условия

Примечание №1: для нахождения A_n или B_n требуется знать, что: Если Φ_n(x) ортогональная система функций:

Стационарная неоднородность в уравнении или краевом условии

Стационарная неоднород-

ность (не зависит от t) в уравнении или краевом условии, начальные условия - произвольны

Выделяем стационарное решение, т. е. ищем решение в виде:

Неоднородности общего вида

I)Начальные и краевые условия нулевые.

Ищем собственные функции соответствующие однородной задаче: Φ_n(x) (см. метод разделения переменных), решение U(x,t) раскладываем в ряд по собственным функциям по теореме Стеклова:

тогда для Ψ_n(t) получаем задачу Коши:

Примечание №2: В ряде случаев неоднородность можно разложить в ряд по тем же собственным функциям задачи Штурмана-Лиувиля: коэффициенты f_n(t) находим обычным способом (см. примечание №1), тогда решение находим следующим способом:

Нахождение частного решения неоднородного дифференциального уравнения: P_s, Q_s – полиномы степени «s».

то частное решениеимеет следующий вид:

,если не корень; ,если корень кратности «к».

Нахождение общего решения однородного дифференциального уравнения:

I)Линейное однородное уравнение первого порядка:

решается методом разделения переменных.

II)Линейное однородное уравнение второго порядка:

ищем решение в виде: тогда получаем характеристическое уравнение :

1) 2)

3) или

II)Не нулевые начальные условия.

Ищем решение в виде:U(x,t)=υ(x,t)+ω(x,t)

III)Не нулевые краевые условия

Подбираем υ(x,t) такое, чтобы оно удовлетворяло краевым условиям, и ищем решение в виде: , g(x,y) – новая неоднородность