16)Вычисл. Пи-1

Если S задана ур-ем F(x,y,z)=0, то вектор нормали любой точки этой пов-ти имеет коорд. (F’_x ,F’_y ,F’_z). ₀= = ; ₀(cos α,cos β,cos γ). Если взять бесконечно малый эл-нт площади ds и проецировать его на коор-ые плоскости, то площади этих проекций будут равны: xOy:dydz=cosαds; xOz:dxdz=cosβds; yOz=dxdy=cosγds

1)Пусть пов. S задана ур-ем: z=z(x,y), то пов-т проец-ся на xOy, то вектор нормали: z-z(x,y)=0. (-z’_x ,-z’_y ,1); ;

ds= = . Пусть D_xy–проекция пов-ти S на пл-ть =

2) и 3) по аналогии.

19)Векторное поле. Поток векторного поля

Если в кажд. т. М прост-ой обл-ти М V опр-ён вектор (М),то обл-ть V–векторное поле M(x,y,z).

Поток векторного поля через ориентированную поверхность S –величина П_S( = )ds, –вектор нормали, единичный, на выбранной стороне поверхности . Пусть поле –поле скоростей частиц несжимаемой жидкости которая протекает через некот. ориентров. пов-ть S. Тогда поток поля через пов-ть S - это кол-во жидкости, протекающей в ед-цу времени через пов-ть S в сторону вектора П_S( =

20.Числ. Ряды и его сумма.Св-ва сход. Рядов

Рассм.числ. посл-ть а₁ , а₂ , а₃ ,…, а_n ,… а_n

Опр.1. Выр-е вида (1) наз-ся числ. рядом

а₁ , а₂ ,… - члены ряда

а_n - общий член ряда

Опр.2. Сумма наз-ся n-й частичной суммой ряда.

Опр.3. Если сущ. конечный предел посл-ти частичных сумм (т.е. ), то это число S наз-ют суммой числ. ряда 1 и говорят при этом, что ряд сходится.

Если предел не сущ. или равен , то ряд 1 расходится.

Св-ва сход. рядов

1. сходимость ряда не нарушится, если произвольным образом изменить (добавить, отбросить, перестав. местами) конечное число членов ряда

2. Сход. ряд можно почленно умножить на любое число, при этом если сумма ряда равна S, то сумма ряда с членами будет

Общий множитель можно вынести за знак суммы 3. Сход.ряды можно почленно складывать и вычитать

Если , , то оба ряда должны сходиться.

21. Необход. Усл-е сход-ти ряда. Гармонич. Ряд

Т.1.Необход. усл-е сх. ряда. Если ряд (1) сход., то .

Док-во. Пусть (1) сх.

Следствие.Если , то (1) – расх.

Пр.1. - расх.

Пр.2. - гармонич. ряд

Опр.1. Остатком ряда 1 наз-ся выр-е

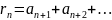
Если ряд сх, то .

Т.2. Ряд (1) сх.

Док-во.

(1) сх.

установим расх. гарм. ряда

ряд расх.

22. Признаки сравнения сх. Рядов с положит. Членами.

,

Т1. Числ. Ряд с полож. Членами сх. тогда, когда посл-ть его частичных сумм ограничена.

Т2.(признак сравнения) Пусть даны 2 ряда с полож. членами (1), (2)

, 0< тогда: 1.если (2) сх.

2.если (1) расх.

Т3. Предельный признак сравнения. Пусть для рядов (1) и (2) с полож. членами сущ. Конечный предел Тогда ряды (1), (2) ведут себя одинаково в смысле сходимости.

Опр.1 Пусть ряд (2)сх.,тогда

тоже сх. сх. по признаку сравнения

Опр.2 Пусть (2) расх. (1) расх.по признаку сравнения.