1.Двойной интеграл, геометр. и физ. смысл.

Пусть ограниченная ф-ия z=f(x,y) определена в некоторой замкнутой области D плоскости xOy.

1.Разобьём область D произвольно на конечное число n элементарных областей (ячеек) D₁,D₂,…,D_n ,не имеющих общих внутренних точек, и обозначим площади этих ячеек Δσ₁, Δσ₂,…, Δσ_n, а диаметры ячеек (максимальное расстояние между двумя точками на границе ячейки) d₁, d₂,…,d_n.Пусть d ­– наибольший из диаметров ячеек.

2.Выберем в каждой из этих ячеек D_i произвольную точку M_i(x_i,y_i)

и вычислим значение f (x_i , y_i) (i = ) .

3.Составим сумму вида , которая называется интегральной суммой для функции f(x,y) по области D.

Предел интегральной сумы при d→0 (n→∞) называется двойным интегралом по области D от функции f(x,y) и обозначается так: или , т.е. = = , (1) где D–область интегрирования.

Если ф-я f(x,y) непрерывна в замкнутой области D, то двойной интеграл существует (т.е. существует предел интегральной суммы) и не зависит от способа дробления области D на элементарные ячейки D_i и выбора точек M_i(x_i,y_i) в них (теорема существования двойного интеграла).

Геометрический смысл двойного интеграла: если f(x,y)≥0 в области D, то двойной интеграл (1) численно равен объёму цилиндрического тела Q с основанием D и образующей, параллельной оси Oz, которое ограничено сверху поверхностью z=f(x,y). В частном случае, когда f(x,y)=1, двойной интеграл (1) равен площади области D,т.е.

.

Физический смысл двойного интеграла: если область D–плоская пластинка, лежащая в плоскости xOy, с поверхностной плотностью γ(x,y), то массу пластинки находят по формуле

m=

2.Основные свойства дв. Интегралов

1.Линейность.

2.D=D₁ D₂ D1 D₂ не имеют общих внутренних точек, то dxdy

3.Если f(x,y)≥ 0, в D=>

4.Если f(x,y) ≥g(x,y) в D =>

5.Пусть ф-я f(x,y) непрер. в огранич. замкн. области D и m=

M= f(x,y), m· ≤ ≤M·

6.Теорема о среднем .Если ф-я f(x,y) непрер. в огранич. замкн. обл. D, то в этой обл. найд-ся такая точка (x₀,y₀) с D, что =f(x₀,y₀)· . Величина назыв-ся средним знач-ем ф-ии f(x,y) в обл. D.

3.Вычисл. Дв. Интегр. В прямоуг. Коорд.

Опр. Обл. D назыв-ся стандартной относит-но оси Oy, если она ограничена слева и справа прямыми х=a и х=b, а сверху и снизу графиками непр. ф-ий y=y₂(x) (сверху, линия выхода) и y=y₁(x) (снизу, линия входа). Эти графики не пересекаются. Если обл. D явл-ся стандартной для Oy, то (1). Интегральное равенство (1) (справа) называется повторн. интегралом, а – внутренним интегралом.

Вычисление повторного следует начинать с вычисления внутреннего, в котором переменную x надо принять при интегрировании за постоянную величину. Рез-тат интегр-ия будет некоторой ф-ией от х, кот-ая интегрируется затем по отрезку [a,b]. В рез-те получается некоторое постоянное число.

Если область D явл-ся стандартной относительно Ox, двойной интеграл вычисляется по формуле =

4.Криволин. Коорд. На плоск-ти. Замена перем-ых в дв. Коорд.

Пусть в обл. D на плоскости xOy заданы 2 непр. ф-ии и пусть систему (1) можно однозначно разрешить относительно x,y. Если между областями D и D*, лежащими в плоскостях xOy и uO₁v, установлено соотношениями (2) взаимно однозначное отображение, причём ф-ии (2) имеют непрерывные частные производные первого порядка в обл. D* и якобиан преобразования в обл. D* не обращается в нуль, т.е. , то имеет место след-ая формула замены переем-ых в дв.интеграле: = , где выражение называется элементом площади в криволинейных координатах.

5.Вычисление дв. Интегр. В полярн. Коорд.

В полярных коорд. формулы имеют вид: x=rcosφ; y=rsinφ (1). Формулы (1) связывают прямоугольные координаты x,y с полярными коорд. r, φ при условии, что полюс помещён в начало координат и полярная ось направлена вдоль оси Ox. В этом случае якобиан преобразования J= -r. Следовательно, , и поэтому формула =

примет вид rsinφ)rdrdφ.

Переход к полярн. координатам: 1)Изображаем пл. D на обл. xOy

2)Записываем ур-ия линий, огранич-их обл. D, в палярн. координатах. А также записываем подынтегральн. ф-ии в полярных координатах.

3)Определяем границы φ₁ и φ₂ изменения палярного угла.

4)Определяем нижний и верхний пределы изменения переменной r. Из начала коорд. через обл. D проводим луч.Линия через котор. мы входим в обл. D –r_н= r_н(φ), когда выходим, то r_в= r_в(φ). Если начало коорд. лежит в обл. D или на её границе, то r_н=0.

5)Сводим двойной интеграл к повторному по формуле: = .

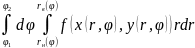Замечание: если среди линий, ограничивающих обл. D имеются эллипсы , k N, то переходим к обобщённым полярным координатам.

Обобщёнными полярными координатами называют переменные r и φ, связанные с прямоугольными координатами x и y формулами: x=ar ·cosφ; y=br·sinφ, где r≥0; 0≤φ≤2π; a>0; b>0; a≠b.

Для обобщённых полярных коорд. , =abr и формула (2) принимает вид = ab .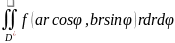

6)3-ой интеграл и его физич. смысл.

1)Разобьём область V некоторыми поверхностями на n элементарных ячеек.

2)Выберем в каждой i-ой элемент. ячейке точу (x_i,y_i,z_i).

3)Составим сумму вида ,где (i = ) –объёмы элементарных областей V_i , на которые разбита обл. V .

Опр.1Сумма (1) назыв-ся интегральной суммой от f(x,y,z) по обл. V. Обозначим через d наибольший из диаметров элементарных областей. Опр2. Если сущ-ет бесконечн. предел интегральн. суммы (1), котор. не зависит ни от способа разделения обл. Vна элементарн. ячейки, ни от способа выбора точек в них, то этот предел называется 3-ным интегралом по обл. V от ф-ии f(x,y,z) и обозначается = , dv–элемент объёма.

Физ. смысл.: Если в простр. облл. V распределена некоторая масса m с плотностью ρ(x,y,z), то масса тела, занимающего обл. V, будет равна .