28. Регрессионные модели с переменной структурой (фиктивные переменные).
. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иныецифровые метки, т.е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Рассмотрим
применение фиктивных переменных для
функции спроса. Предположим, что по
группе лиц мужского и женского пола
изучается линейная зависимость
потребления кофе от цены. В общем виде
для совокупности обследуемых уравнение
регрессии имеет вид: 
,
где y – количество потребляемого
кофе; x– цена.
Аналогичные
уравнения могут быть найдены отдельно
для лиц мужского пола: 
и
женского пола: 
.
Различия
в потреблении кофе проявятся в различии
средних 
и 
.
Вместе с тем сила влияния 
на 
может
быть одинаковой, т.е. 
.
В этом случае возможно построение общего
уравнения регрессии с включением в него
фактора «пол» в виде фиктивной переменной.
Объединяя уравнения 
и 
и,
вводя фиктивные переменные, можно прийти
к следующему выражению:
,
где 
и 
–
фиктивные переменные, принимающие
значения:
29. Экономическая интерпретация многофакторной регрессионной модели.
на
основе коэффициентов регрессии нельзя
сказать, какой из факторных признаков
оказывает наибольшее влияние на
результативный признак, так как
коэффициенты регрессии между собой
несопоставимы, поскольку они измерены
разными единицами. Чтобы иметь возможность
судить о сравнительной силе влияния
отдельных факторов и о тех резервах,
которые в них заложены, должны быть
вычислены частные коэффициенты
эластичности 
,
а также бета-коэффициенты 
.
частных коэффициентов эластичности, которые рассчитывают по формуле:
Частный коэффициент эластичности показывают, на сколько процентов в среднем изменяется признак-результат Y с изменением признака-фактора Х на один процент от своего среднего уровня при фиксированном положении других факторов модели
Для определения факторов, в развитии которых заложены наиболее крупные резервы улучшения изучаемого показателя, необходимо учесть различия в степени варьирования вошедших в уравнение факторов. Это можно сделать с помощью β-коэффициентов, которые вычисляют по формуле:
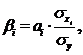
где 
- среднее
квадратическое отклонение i-го фактора;
-
среднее квадратическое отклонение
показателя.
30. Понятие мультиколлинеарности, ее значение при отборе факторов.
Мультиколлениарность факторов – тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат, которая затрудняет оценивание регрессионных параметров
Причинами возникновения мультиколлинеарности между признаками являются:
1. Изучаемые факторные признаки, характеризуют одну и ту же сторону явления или процесса.;
2. Использование в качестве факторных признаков показателей, суммарное значение которых представляет собой постоянную величину;
3. Факторные признаки, являющиеся составными элементами друг друга;
4. Факторные признаки, по экономическому смыслу дублирующие друг друга.
5. Одним из индикаторов определения наличия мультиколлинеарности между признаками является превышение парным коэффициентом корреляции величины 0,8 (rxi xj) и др.
Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон, и в результате нельзя будет оценить воздействие каждого фактора в отдельности.