11. Первичная статистическая обработка при построении эконометрической модели.

В большинстве случаев обработку целесообразно начать с составления таблиц (сводных таблиц) полученных данных. В таблицу можно свести не только числовые данные. К данным качественного характера также могут быть применены простейшие способы количественной обработки. Для всей выборки и отдельных подвыборок могут быть подсчитаны частоты встречаемости (количество случаев появления события), а затем и частости (относительные частоты, т.е. частоты, деленные на количество испытаний) интересующих вас индикаторов, проявлений некоторого вида. В виде чисел в таблицу можно вписать информацию и о тех параметрах выборки, которые предположительно могут оказаться значимыми факторами, но имеются у вас в качественных показателях. Наиболее простыми операциями могут быть: числовое кодирование и перевод качественных показателей в ранги. После создания таблицы на бумаге или компьютере необходимо проверить качество полученных данных. Для этого часто достаточно внимательно осмотреть массив данных. Начать проверку следует с выявления ошибок (описок), которые заключаются в том, что неправильно написан порядок числа. 

12. Построение двухмерной линейной модели корреляционно-регрессионного анализа.

Линейная регрессия сводится к нахождению уравнения вида   Построение линейной регрессии сводится к оценке ее пара­метров а и b. МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений ре­зультативного признака (у) от расчетных (теоретических)  ми­нимальна: 

Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минималь­ной:

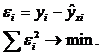
Решается система нормальных уравнений:

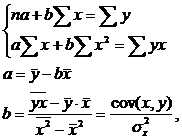
где   ,   и    - средние значения факторов Х, Y и их произведения;

         cov(x,y) – ковариация признаков.

При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэф­фициента корреляции.

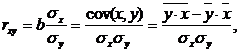
13. Проверка значимости коэффициентов простой линейной регрессии и адекватности регрессионной модели.

1. F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы H(нулевой) 0 остатистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт  и критического (табличного) Fтабл значений F-критерия Фишера. Fфактопределяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

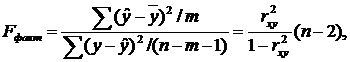
где   n – число единиц совокупности;

        m – число параметров при переменных x.

Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a. Уровень значимости a  –  вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a принимается равной 0,05 или 0,01.

Если  Fтабл< Fфакт, то H0  – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если  Fтабл> Fфакт, то H0 – гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.

2.  t-критерий Стьюдента используется для оценки статистической значимости коэффициентов регрессии и коэффициента  корреляции.

В качестве основной гипотезы вы­двигают гипотезу H0 о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции.

Фактические значения t-критерия определяются по формулам:

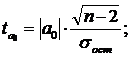
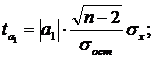
где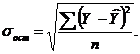   

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

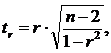
где r - оценка коэффициента корреляции, полученная по наблюдаемым данным. tтабл  остается прежним.