
- •Атмосферный воздух. Классификация, история и
- •1.1. Атмосферный воздух и его компоненты
- •1.2. Стандарты основных продуктов разделения воздуха
- •1.3. Области применения продуктов разделения воздуха
- •1.4. Классификация воздухоразделительных установок (вру)
- •1.5. Основные элементы и блоки вру
- •1.6. Краткая история развития воздухоразделительных установок
- •1.7. Особенности современных воздухоразделительных установок (вру)
- •2.2. Потери холода в криогенных циклах
- •2.3. Криогенные циклы
- •2.3.1. Криогенный дроссельный цикл
- •Криогенный дроссельный цикл с предварительным внешним охлаждением
- •2.3.3. Детандерный криогенный цикл высокого давления Гейляндта
- •2.3.4. Детандерный криогенный цикл среднего давления Клода
- •2.6. Детандерный криогенный цикл низкого давления Капицы
- •2.7. Детандерный криогенный цикл двух давлений
- •2.8. Детандерный криогенный цикл низкого давления с совмещенным циркуляционным контуром
- •2.9. Примеры расчета эффективности работы различных криогенных циклов
- •2.10. Анализ результатов расчета различных криогенных циклов
- •3.2. Физические основы разделения воздуха.
- •3.2.1. Упругость насыщенных паров кислорода и азота
- •3.2.2. Экспериментальные кривые равновесия
- •3.2.3. Диаграмма равновесных кривых х-у смеси кислород – азот при различных давлениях
- •3.2.4. Номограмма т-p-I-х-у Герша-Цеханского для системы кислород – азот
- •3.2.5. Диаграмма I - X для системы кислород-азот
- •3.3. Ректификация воздуха, принцип ректификации
- •3.4. Колонны для разделения воздуха
- •Колонна однократной ректификации
- •Колонна двукратной ректификации
- •3.5. Расчет числа теоретических тарелок в ректификационных колоннах
- •Методом Мак-Кэба и Тиле
- •3.6. Графические расчеты процессов ректификации и определение числа теоретических тарелок при помощи I -х диаграммы (метод Пуаншона)
- •В колонне в I-х диаграмме
- •Пример расчета числа теоретических тарелок в колонне двукратной ректификации с помощью у-х и I-х диаграмм
- •4. Принципиальные технологические схемы современных вру
- •4.1. Особенности разработки технологических схем современных вру
- •4.2. Вру большой производительности низкого давления нового поколения
- •4.3. Вру среднего давления
- •4.4. Вру двух давлений
- •4.5. Вру высокого давления
- •4.6. Вру низкого давления малой и средней производительности с совмещенным циркуляционном контуром для выдачи жидких продуктов или газообразных под высоким давлением
- •4.7. Технологическая схема аргонного блока вру с получением чистого аргона методом низкотемпературной ректификации
- •4.8. Получение чистых криптона и ксенона в вру
- •5. Основные блоки и аппараты вру
- •5.1. Блок очистки и осушки воздуха
- •5.1.1. Методы очистки и осушки воздуха
- •5.1.2. Очистка воздуха от двуокиси углерода с помощью сорбентов
- •5.1.3. Очистка воздуха от примесей ацетилена
- •5.1.4. Комплексная очистка воздуха от примесей , и
- •5.1.5. Схема и устройство блока комплексной осушки и очистки воздуха (бкоо)
- •5.1.6. Методика расчета адсорбционного блока осушки и очистки воздуха от примесей паров влаги, углекислоты и ацетилена
- •Расчет процесса десорбции
- •5.2. Определение основных конструктивных размеров ректификационных колонн вру
- •Бинарной смеси
- •Тарелки; 3 – наружная обечайка; 4 - люк
- •Устройствами различных типов:
- •5.3. Определение основных конструктивных размеров конденсаторов-испарителей
- •С внутритрубным кипением
- •Р ис. 5.9. Зависимость кратности циркуляции от различных факторов:
3.5. Расчет числа теоретических тарелок в ректификационных колоннах
Для определения числа теоретических тарелок в ректификационных колоннах применяются несколько методов, но наибольшее распространение получили графические методы Мак-Кэба и Тиле, и Пуаншона, которые отличаются своей простотой и наглядностью. При графическом расчете методом Мак-Кэба и Тиле пользуются диаграммой равновесных состояний х-у, но при этом делают допущение, что скрытые теплоты парообразования для одного моля обоих компонентов равны между собой. Это позволяет принимать, что количества поднимающихся паров G и стекающей жидкости-флегмы g по высоте колонны остаются постоянными величинами.
Определение числа теоретических тарелок в нижней концентрационной
колонне методом Мак-Кэба и Тиле
Нижняя концентрационная (укрепляющая) колонна предназначена для получения нижекипящего компонента. Процесс ректификации в нижней колонне протекает при определенном избыточном давлении.
Пусть
в нижнюю часть концентрационной
колонны (рис. 3.8) непрерывно подается
сжатый частично ожиженный воздух в
количестве М
под давлением
![]() .
Доля жидкости,
подаваемой в насыщенном состояние,
составляет
.
Доля жидкости,
подаваемой в насыщенном состояние,
составляет
![]() с концентрацией
с концентрацией
![]() нижекипящего
компонента, доля пара в равновесном
состоянии с жидкостью составляет
нижекипящего
компонента, доля пара в равновесном
состоянии с жидкостью составляет
![]() с концентрацией
с концентрацией
![]() нижекипящего
компонента.
нижекипящего
компонента.
Из
верхней части колонны непрерывно
отводится нижекипящий компонент Д
с концентрацией
![]() ,
называемый
дистиллятором. Пары, поднимающиеся
по колонне в количестве G
и уходящие
из колонны в верхней части, полностью
конденсируются в конденсаторе К.
Часть
сконденсированной жидкости в
количестве g
с концентрацией
возвращается
в колонну и в качестве флегмы стекает
по колонне. Другая часть в количестве
Д
и концентрацией
отводится
в виде продукта.
,
называемый
дистиллятором. Пары, поднимающиеся
по колонне в количестве G
и уходящие
из колонны в верхней части, полностью
конденсируются в конденсаторе К.
Часть
сконденсированной жидкости в
количестве g
с концентрацией
возвращается
в колонну и в качестве флегмы стекает
по колонне. Другая часть в количестве
Д
и концентрацией
отводится
в виде продукта.
В
нижней части колонны из нее непрерывно
отводится жидкая смесь в количестве R
и концентрацией
![]() нижекипящего
компонента, называемая кубовой
жидкостью.
нижекипящего
компонента, называемая кубовой
жидкостью.
Для определения числа теоретических тарелок и концентрации уходящих жидкостей-продуктов разделения составим материальные балансы:
1) в отношении общего количества, поступающего на разделение смеси;
2) в отношении нижекипящего компонента – азота:
с одной стороны, для входящей смеси:
![]() , (3.10)
, (3.10)
![]() .
(3.11)
.
(3.11)
С другой стороны, для продукта разделения:
![]() ,
(3.12)
,
(3.12)
для любого сечения колонны:
![]() ,
(3.13)
,
(3.13)
![]() , (3.14)
, (3.14)
![]() , (3.15)
, (3.15)
![]() ,
(3.16)
,
(3.16)
![]() .
(3.17)
.
(3.17)
Отношение
![]() называется флегмовым числом.
называется флегмовым числом.
Из (3.14) и (3.15) найдем соотношение:
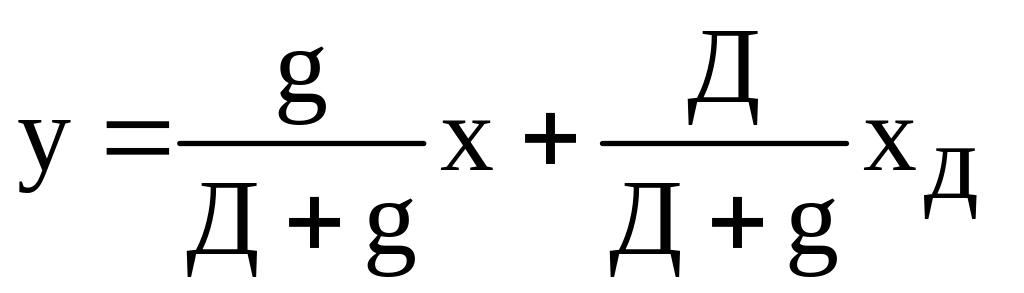 .
(3.18)
.
(3.18)
Разделив числитель и знаменатель на величину Д, получим
![]() .
(3.19)
.
(3.19)
Из
последнего уравнения величины
![]() и
и
![]() являются постоянными, поэтому в системе
координат
являются постоянными, поэтому в системе
координат
![]() оно представляет собой уравнение прямой
линии. Здесь х – концентрация низкокипящего
компонента – азота в жидкости в молевых
процентах, откладывается по оси абсцисс,
а у – концентрация низкокипящего
компонента – азота в паре в молевых
процентах, откладывается по оси ординат.
оно представляет собой уравнение прямой
линии. Здесь х – концентрация низкокипящего
компонента – азота в жидкости в молевых
процентах, откладывается по оси абсцисс,
а у – концентрация низкокипящего
компонента – азота в паре в молевых
процентах, откладывается по оси ординат.
Эта
прямая при х = 0 имеет координату
![]() при х =
из уравнения (3.19) следует, что у =
.
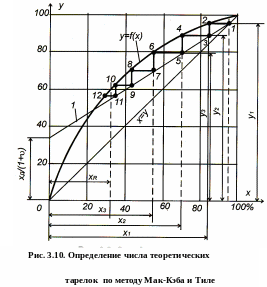
Построение этой линии изменения рабочей
концентрации показано на рис. 3.10.
при х =
из уравнения (3.19) следует, что у =
.
Построение этой линии изменения рабочей
концентрации показано на рис. 3.10.
Прямая
1, построенная по уравнению (3.19), и кривая
равновесного состояния у = f(х)
при давлении в колонне показывают
составы пара и жидкости в любом поперечном
сечении колонны при данной флегме
![]() и для количества дистиллята Д с содержанием
нижекипящего компонента
,
то есть определяют содержание азота в
жидкости, стекающей с тарелки, и в паре,
поднимающемся на данную тарелку с
нижерасположенной тарелки.
и для количества дистиллята Д с содержанием
нижекипящего компонента
,
то есть определяют содержание азота в
жидкости, стекающей с тарелки, и в паре,
поднимающемся на данную тарелку с
нижерасположенной тарелки.
Если
предположить, что в конденсаторе не
происходит изменения концентрации, то
есть содержание азота в жидкости
-дистилляте
и пара, поднимающегося с верхней тарелки
,
одинаковы,
то на рис. 3.10 их составы обозначаются
т.1 Составу пара, уходящего с верхней
тарелки с концентрацией
,
соответствует
равновесное содержание жидкости с
концентрацией
![]() ,
стекающей
с верхней тарелки в т.2 на кривой равновесия
,
стекающей
с верхней тарелки в т.2 на кривой равновесия
![]() .
Составу
жидкости, стекающей с первой на вторую
тарелку, и пара, выходящего со второй
тарелки, соответствует на прямой линии
концентрации т.3.
.
Составу
жидкости, стекающей с первой на вторую
тарелку, и пара, выходящего со второй
тарелки, соответствует на прямой линии
концентрации т.3.
Т.4, лежащей на кривой равновесия и имеющей ординату т.3, соответствует пар, выходящий со второй тарелки, и жидкость, стекающая на третью тарелку.
Продолжая
построение указанным выше способом,
можно найти число
ступеней
между прямой, проведенной по уравнению
(3.19) и кривой равновесия до абсциссы,
соответствующей кубовой жидкости
![]() .
.
Число полученных ступеней дает число теоретических тарелок, полученных из условия достижения равновесия между паром и жидкостью на каждой тарелке, то есть при коэффициенте обогащения S = 1.
|
(3.20) |
Коэффициент
обогащения равен отношению разности
действительной концентрации
нижекипящего компонента, поступающего
и уходящего пара с тарелки, к разности
концентраций пара, находящегося в
равновесном состоянии с уходящей
жидкостью
![]() и поступающего пара
.
и поступающего пара
.
Под коэффициентом обогащения S = 1 понимают коэффициент, когда пар, прошедший через тарелку, будет находиться в равновесии со стекающей жидкостью.
Уравнения
(3.10)-(3.13) позволяют определить концентрацию
![]() выходящей
кубовой жидкости при заданных концентрациях
,
выходящей
кубовой жидкости при заданных концентрациях
,![]() ,
,![]() и
и
![]() .
.
Определение числа теоретических тарелок в верхней колонне двукратной
ректификации, состоящей из концентрационной и отгонной секций, методом мак-кэба и тиле
С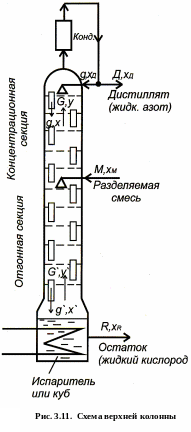 хема
верхней колонны, состоящей из
концентрационной и отгонной секции,
показана на рис. 3.11. В среднюю часть
ректификационной колонны поступает
разделительная смесь в количестве
М
и
концентрацией
(в
случае разделения воздуха в колонне
двукратно ректификации в качестве
такой разделительной смеси является
кубовая жидкость, поступающая из куба
нижней колонны).
хема
верхней колонны, состоящей из
концентрационной и отгонной секции,
показана на рис. 3.11. В среднюю часть
ректификационной колонны поступает
разделительная смесь в количестве
М
и
концентрацией
(в
случае разделения воздуха в колонне
двукратно ректификации в качестве
такой разделительной смеси является
кубовая жидкость, поступающая из куба
нижней колонны).
Из
верхней части колонны отводится
газообразный нижекипящий компонент-азот
в количестве G
и концентрацией
![]() ,
который
конденсируется в конденсаторе К,
и часть его
возвращается в колонну в количестве
g
и концентрацией
и стекает
по тарелкам колонны в качестве флегмы,
а другая часть отводится в качестве
продукта-дистиллята (жидкий азот) в
количестве Д
и концентрацией
.
,
который
конденсируется в конденсаторе К,
и часть его
возвращается в колонну в количестве
g
и концентрацией
и стекает
по тарелкам колонны в качестве флегмы,
а другая часть отводится в качестве
продукта-дистиллята (жидкий азот) в
количестве Д
и концентрацией
.
Из нижней части колонны отводится остаток - жидкий кислород в количестве R
и концентрацией .
, |
где
![]() - флегмовое число для концентрационной
части колонны.
- флегмовое число для концентрационной
части колонны.
Проведя по этому уравнению прямую линию в диаграмме состояния х-у и проделав соответствующие построения в ней, как на рис. 3.10, определим число теоретических тарелок в концентрационной части колонны (рис.3.12).
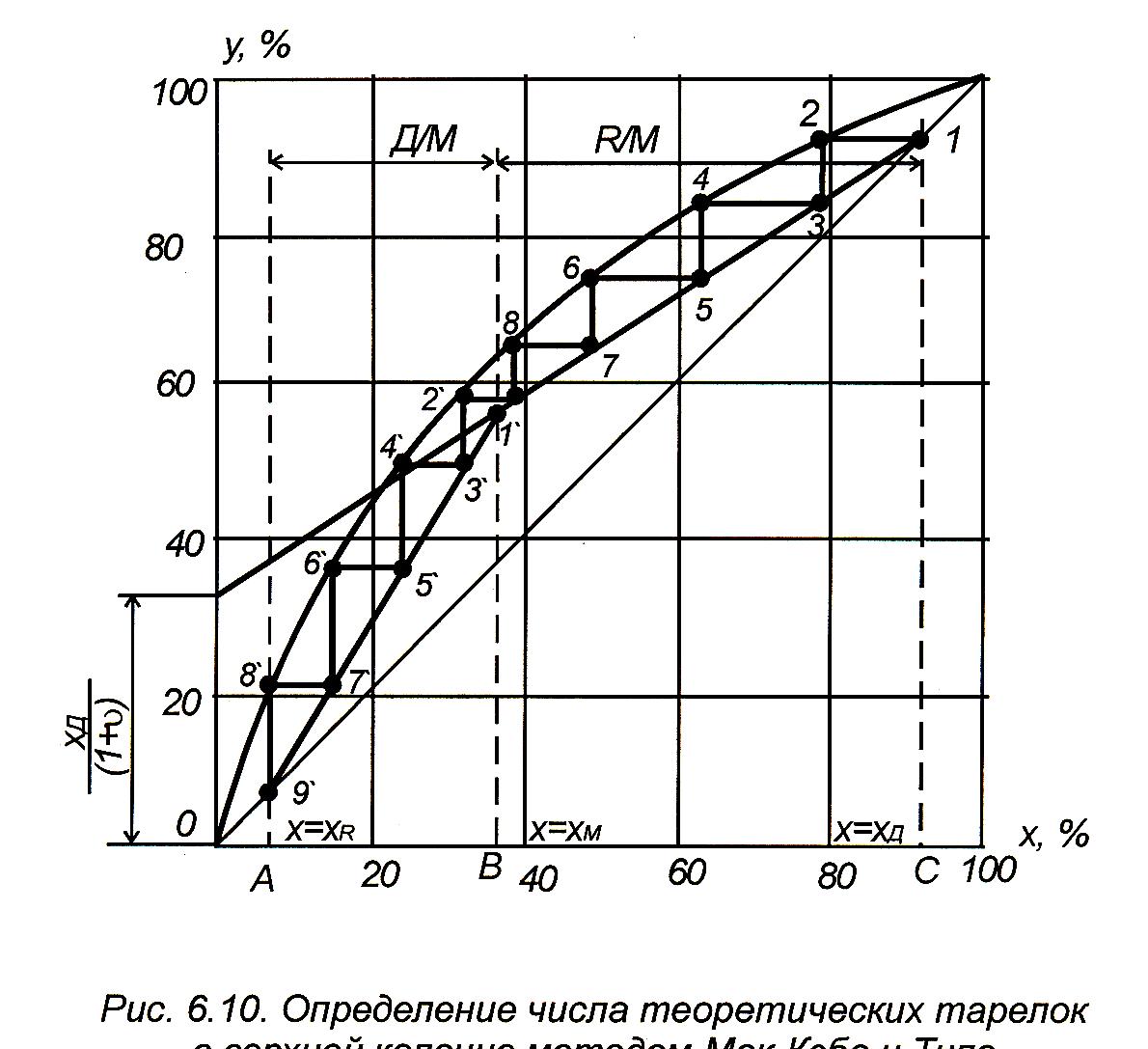
Рис. 3.12. Определение числа теоретических тарелок в верхней колонне

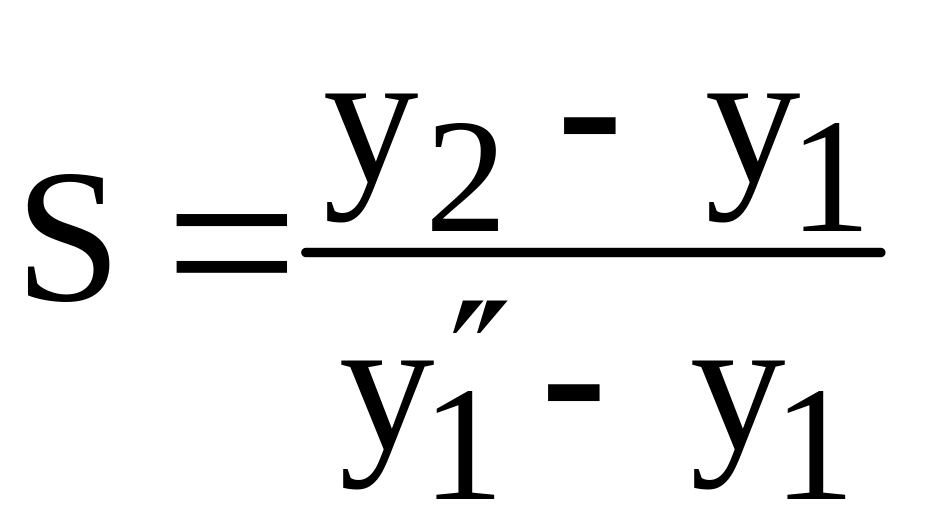 .
.