54. Теорема Ролля
Теорема: Пусть на [a, b] определена функция f(x), причем:
f(x) непрерывна на [a, b];
f(x) дифференцируема на (a, b);
f(a) = f(b).
Тогда существует точка C(a, b), в которой f ’(c) =0.
Док-во: Так как функция f(x) непрерывна на [a, b], то она достигает на этом отрезке максимальное значение M и минимальное значение m, т. е. существуют такие точки X1, X2[a, b], что f(X1) = m, f(X2)=M , и выполняется неравенство m f(x) M.
Возможны 2 случая: 1) m=M ; 2)m<M.
В первом случае f(x) = const = m = M. Поэтому производная f ’(x) = 0 в любой точке [a, b], и теорема доказана.
Во втором случае так как f(a) = f(b), то хотя бы одно из двух значений M и m, не принимается на концах отрезка [a, b], т. е. существует точка C(a, b), в которой функция f(x) принимает наибольшее или наименьшее значение на интервале (a, b). В этом случае, так как f(x) дифференцируема в точке C, то (по Т Ферма) f ’(x) =0.
Геометрический смысл: Между двумя точками кривой, заданной уравнением (где функция f(x) непрерывна на [a, b], дифференцируема внутри этого отрезка), с равными ординатами всегда найдется, по крайней мере, одна точка, в которой касательная к кривой параллельна оси ОХ.
55. Теорема Лагранжа
Теорема: Пусть на [a, b] определена функция f(x), причем:
f(x) непрерывна на [a, b];
f(x) дифференцируема на (a, b).
Тогда существует точка C(a, b) такая, что справедлива формула (f(b) – f(a))/(b – a) = f ’(c).
Док-во: Введем в рассмотрение вспомогательную функцию на [a, b].
Функция F(x) удовлетворяет всем трем условиям теоремы Ролля:
F(x) непрерывна на [a, b] (как разность непрерывных функций f(x) и линейной функции
F(x) дифференцируема на (a, b), т. е. внутри [a, b] имеет производную, равную
F(a) =0 и F(b) =0, т. е. F(b) = F(a).
(По
Т Р) Существует точка C(a,
b)
такая, что F’(c)
=0, т. е.
.
Отсюда получаем
Геометрический смысл: На кривой, являющейся графиком функции Y=f(x), удовлетворяющей условиям теоремы Лагранжа, существует точка (по крайней мере, одна), в которой касательная параллельна хорде АВ.
56. Теорема Коши
Теорема: Пусть функции f(x) и g(x) непрерывны на [a, b] и дифференцируемы на (a, b). Пусть, кроме того, g’(x) 0. Тогда существует точка C(a, b) такая, что справедлива формула
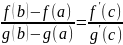
Док-во: Докажем сначала, что g(b) – g(a) 0, т. е., что формула имеет смысл. Действительно, если допустить, что g(b) = g(a), то (по Т Р) для функции g(x) точка (a, b), в которой g’()=0.А это противоречит условию, что g’(x) 0 на (a, b).
Докажем формулу. Рассмотрим на [a, b] вспомогательную функцию
Нетрудно заметить, что на удовлетворяет условиям теоремы Ролля:
F(x) непрерывна на [a, b];
дифференцируема на (a, b), кроме того, F(b) = 0 и F(a) = 0, т. е. F(a) = F(b) (по Т Р) для функции F(x) точка C, a<C<b, такая, что F’(c) = 0.
Так
как
, то
Учитывая, что g’(x) 0, получаем формулу .
. Правило Лопиталя
Теорема:
Пусть функции f(x)
и g(x)
определены и дифференцируемы в некоторой
окрестности точки a,
за исключением, быть может, самой точки
а.
Пусть, далее,
и g(x)≠0
в указанной окрестности точки а.
Тогда, если существует предел отношения
производных
(конечный или бесконечный), то существует
и предел
,
причем справедлива формула
Док-во:
Пусть {
}
— произвольная последовательность
значений аргумента, сходящаяся к точке
а,
причем
.
Доопределим функции f(x)
и g(x)в
точке а,
положив их равными нулю, т.е. f(a)=g(a)=0.
Тогда, очевидно, функции f(x)
и g(x)
непрерывны на
,
дифференцируемы на (
Таким образом, для f(x)
и g(x)
выполнены все
условия теоремы Коши на
,
т.е. внутри
существует точка
такая,
что
По доопределению, f(a)=g(a)=0, следовательно,
(1)
Пусть
теперь в формуле (1)
.
Тогда, очевидно,
при
.
Так как
Следовательно, при
существует предел и левой части формулы
(1), причем
.
Так как { } — произвольная последовательность значений аргумента, сходящаяся к а, то отсюда заключаем, что существует и