Монотонная функция

f(x) c D монотонно возрастает (не убывает), если

∀ x₁,x₂ ϵ D x₁ <(≤ ) x₂ ==> f(x₁) <(≤ ) f(x₂)

D_a⁺ = {x ϵ D : x > a} D_a^– = {x ϵ D : x < a}

правая предельная точка левая предельная точка

всякая предельная точка является либо правой предельной точкой,

либо левой предельной точкой, либо сразу и той, и другой.

f/_Da+ = f_a⁺(x) f/_Da– = f_a^–(x)

lim_x→a+0 f(x) = lim_x→a f_a⁺(x) lim_x→a-0 f(x) = lim_x→a f_a^– (x)

f(x) D, f(x) D,

∀ x f(x) ≤ M < +∞ ∀ x f(x) ≥ M > –∞

a – левая предельная точка a – правая предельная точка

∃ lim_x→a-0 f(x) = sup_Da– f(x) ∃ lim_x→a+0 f(x) = inf_Da+ f(x)

A – ℰ < f(x_ℰ) ≤ f(x) A ==> |f(x) – A| < ℰ

|f_a^–(x) – A| < ℰ

{x_n} c D, x_n ≠ a, x_n → a

{x_n} c D, x_n → +∞

lim_n→∞ f(x_n) = A

∀ ℰ > 0 ∃ M_ℰ : x ϵ D, x > M ==> |f(x) – A| < ℰ

{x_n} c D, x_n → –∞

lim_n→∞ f(x_n) = A

∀ ℰ > 0 ∃ M_ℰ : x ϵ D, x < M ==> |f(x) – A| < ℰ

{x_n} c D, x_n → +∞

lim_n→∞ f(x_n) = +∞

∀ M ∃ δ>0 : x ϵ D, x≠a, |x – a|< δ ==> f(x) > M

{x_n} c D, x_n → –∞

lim_n→∞ f(x_n) = –∞

∀ M ∃ δ>0 : x ϵ D, x≠a, |x – a|< δ ==> f(x) < M

∀ M D ∩ (M , ∞) or ∀ M ∃ x ϵ D : x > M

состоит из бесконечного числа элементов

f(x), g(x) D, a – предельная точка

∃ lim_x→af(x) = A, lim_x→ag(x) = B

f(x) D, a ϵ D

1. a – изолированная точка множества D ==> f непрерывна в точке a

2. a – предельная точка D ==> f непрерывна в точке a <==> ∃ lim_x→af(x) = f(a)

Функция Дирихле:

1 – x рациональный,

f(x)

0 – x иррациональный.

Определение непрерывности в точке a:

∀ ℰ>0 ∃ δ>0 : xϵD, 0<|x-a|<δ ==> |f(x)-f(a)| < ℰ ,

здесь требование x ≠ a излишне:

∀ ℰ>0 ∃ δ>0 : x ϵ D, |x-a|<δ ==> |f(x)-f(a)| < ℰ

В терминах последовательности:

∀ {x_n} c D, x_n → a ==> f(x_n) → f(a)

Пусть D, f(x), g(x) – непрерывны в точке a ϵ D. Тогда непрерывны в точке a:

1. f(x) ± g(x)

2. f(x) ⋅ g(x)

3. f(x)/g(x) (g(a) ≠ 0)

4. |f(x)|

Любой полином будет непрерывной функцией:

f(x) = x:

x² = x⋅x

x³ = x⋅x²

…

xⁿ = x⋅x^n-1

_k=0Σⁿ a_k⋅x^k = P(x)

P(x)/Q(x)

|sinx| ≤ |x|, |x| ≤ π/2

k ≤ |x|,

|sinx| ≤ k ≤ |x|

lim_x→asinx = sina

0 ≤ |sinx – sina| = |2⋅sin[(x-a)/2]⋅cos[(x+a)/2]| ≤ 2⋅|(x-a)/2|⋅1 = |x-a|

0 ≤ |sinx – sina| ≤ |x-a|

f(x), D g(y), Δ

f[D] c Δ

h(x) = g(x), D

Если f непрерывна в точке a ϵ D g непрерывна в точке b = f(a) ϵ Δ, тогда h(x) непрерывна в точке a.

∀ ℰ>0 ∃ σ>0 : y ϵ Δ, |y-b| < σ ==> |g(y)–g(b)| < ℰ

Доказательство:

ℰ>0 ∃ σ>0 : y ϵ Δ, |y-b| < σ ==> |g(y)–g(b)| < ℰ

σ>0 ∃ δ : xϵD, |x-a|<δ ==> |f(x)–f(a)| < σ

∀ ℰ>0 ∃ δ>0 : xϵD, |x-a|<δ ==> |f(x)–f(a)| < σ ==> |g(f(x))–g(b)| < ℰ

|f(x)–b| |h(x)–h(a)| (т.к. g(b)=g(f(a))=h(a) )

f(x), D

g(y), Δ h(x)=g(f(x))

f[D] c Δ

f непрерывна в точке a, g непрерывна в точке b=f(a) ==> h(x) непрерывна в точке a

lim_x→ag(f(x)) = g(lim_x→af(x)). Доказано.

Теорема о пределе суперпозиции

f(x), D

g(y), Δ

f[D] c Δ , a – предельная точка D

∃ lim_x→af(x) = b ϵ Δ, g непрерывна в точке b ==> ∃ lim_x→ag(f(x))=g(b)

limg_x→a(f(x)) = g(b) = g(lim_x→af(x))

f’(x) непрерывна в точке a, f(a) = b, g непрерывна в точке b

f(x), x ≠ a

f’(x) =

b, x = a

f’(x) на Dv{a}

lim_x→af’(x) = lim_x→af(x) = b = f’(a) ==> f непрерывна в точке a

Теорема Вейерштрасса

Если функция непрерывна на каком-то множестве, то она непрерывна в каждой точке этого множества.

f(x) [a,b], f непрерывна на [a,b], f(x) ограничена на [a,b]

∀ x ϵ [a,b] |f(x)| ≤ M, 0 < M < ∞

1. x₁ ϵ [a,b] |f(x₁)| > 1

2. x₂ ϵ [a,b] |f(x₂)| > 2

3. x₃ ϵ [a,b] |f(x₃)| > 3

…

14. x_n ϵ [a,b] |f(x_n)| > n

{x_n} c [a,b] {x_nk} : lim_x→∞x_nk = x₀

a ≤ x_n ≤ b a ≤ x_nk ≤ b ==> a ≤ x₀ ≤ b

lim_x→xof(x) = f(x₀)

lim_k→∞f(x_nk) = f(x₀)

|f(x_nk)| > n_k –_k→∞→ ∞

-∞ < inf_[a,b]f(x) ≤ sup_[a,b]f(x) < +∞, sup_[a,b]f(x) = A

∃ x₀ ϵ [a,b] : f(x₀) = A

A-1 ∃ x₁ ϵ [a,b] : A-1 < f(x₁) ≤ A

A-½ ∃ x₂ ϵ [a,b] : A-½ < f(x₂) ≤ A

. . .

A-1/n ∃ x_n ϵ [a,b] : A-1/n < f(x_n) ≤ A

∃ {x_nk} : lim_x→∞x_nk = x₀ ϵ [a,b]

f(x₀) = lim_k→∞f(x_nk) = A = sup_[a,b]f(x)

A – 1/n_k < f(x_nk) ≤ A

Теорема Больцано-Коши:

f, [a,b] – непрерывна, f(a) ⋅ f(b) < 0 (разных знаков) ==> ∃ c ϵ (a,b) : f(c) = 0

Доказательство:

Пусть f((a+b)/2) ≠ 0.

[a₁,b₁], f(a₁)⋅f(b₁) < 0.

Снова разделим пополам данный промежуток.

[a₂,b₂], f(a₂)⋅f(b₂) < 0.

Снова разделим пополам промежуток. Так, продолжая этот процесс, мы либо найдём точку c, где f(c)=0, либо такую точку не найдём, тогда последовательность

[a_n,b_n], f(a_n)⋅f(b_n) < 0,

[a_n,b_n] c [a_n-1,b_n-1],

b_n-a_n = (b-a)/2ⁿ

стремится к нулю lim_n→∞ (b-a)/2ⁿ = 0.

{c} = ∩^∞_n=1 [a_n,b_n]

x_n – конец промежутка [a_n,b_n], f(x_n) > 0

y_n – другой конец [a_n,b_n], f(x_n) < 0

x_n → c, f(x_n) > 0 lim_n→∞f(x_n) = f(c) ≥ 0

==> ==> f(c) = 0.

y_n → c, f(y_n) < 0 lim_n→∞f(x_n) = f(c) ≤ 0

Вывод из теоремы: если функция принимает на концах интервала [a,b] два значения одного знака, рассмотрим функцию y = ξ : f(a) < ξ < f(b). Тогда ∃ c : f(c) = ξ.

Доказательство:

f(a) < f(b), f(a) < ξ < f(b) ==> ∃ c ϵ (a,b) : f(c) = ξ

g(x) = f(x) – ξ, g(a) = f(a) – ξ < 0,

g(b) = f(b) – ξ > 0;

∃ c : g(c) = 0 ==> ∃ c : f(c) – ξ = 0.

<a,b> – некоторый промежуток, т.е.: (a,b), (a,b], [a,b), [a,b].

Пусть f(x) определена и непрерывна на <a,b>. Тогда образ этого промежутка f[<a,b>] – тоже промежуток (это не означает, что функция непрерывна на этом промежутке, если только она не монотонна).

Доказательство:

Пусть A = inf_<a,b> f(x), B = sup_<a,b> f(x). Доказать, что (A,B) c f[<a,b>].

Возьмём ξ ϵ (A,B), ∃ c ϵ <a,b> : f(c) = ξ, т.к.:

A < ξ < B ==> ∃ x₁ ϵ <a,b> : f(x₁) < ξ;

∃ x₂ ϵ <a,b> : f(x₂) > ξ;

Пусть x₁ < x₂. Тогда [x₁,x₂] c <a,b>, f(x) непрерывна на [x₁,x₂], f(x₁) < ξ, f(x₂) > ξ, ==>

==> по т. Больцано-Коши ∃ c ϵ (x₁,x₂) : f(c) = ξ.

Теорема: f определена на <a,b> и монотонна, если область значений f является промежутком, то f – непрерывна.

Доказательство:

Предположим, это не так. Тогда функция имеет разрыв.

Пусть функция возрастет: x₁ < x₂ ==> f(x₁) ≤ f(x₂), c ϵ (a,b) – точка разрыва. Тогда ∃ f(c-0), f(c+0):

f(c–0) = sup_a<x<cf(x) ≤ f(c) x < c ==> f(x) ≤ f(c)

==> ==> f(c-0) ≤ f(c) ≤ f(c+0), т.е. функция в точке c

f(c+0) = inf_c<x<bf(x) ≥ f(c) x > c ==> f(x) ≥ f(c) непрерывна, разрыва нет, противоречие.

f(x) = x^h

f^-1(y) = y^1/n =

Предположим, имеется число a > 0, a^r, r ϵ ℚ. Пусть r = ,

1. a^r = (a^1/n)^m = (a^m)^1/n = a^m/n

2. a^r1⋅a^r2 = a^r1+r2

3. a^-r = 1/a^r

4. r₁ < r₂ ==> a^r1 < a^r2, a > 1

5. r₁ < r₂ ==> a^r1 > a^r2, 0 < a < 1

a > 1, a^r /`

^r = ∞ n = [r], a = 1 + λ, λ > 0

n → ∞, a^r = (1 + λ)² > (1 + λ)ⁿ = 1 + n⋅λ + … > 1 + n⋅λ → ∞

^r = ^-r = ^p = 0, p = -r.

0 < a < 1 :

1. a^r = 1/(1/a^r) = 1/(1/a)^r → 0

2. 1/a > 1, (1/a)^r → ∞

3. (a^r1)^r2 = a^r1⋅r2

a > 1 :

a^1/n – 1 = – 1

= 1 + λ, λ > 0 :

a = (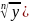 ⁿ = (1 + λ)ⁿ = 1 + n⋅λ + … > 1 + n⋅λ ==> a-1 > n⋅λ ==> λ < (a-1)/n ==> – 1 < (a-1)/n

a^1/n – 1 < (a-1)/n

0 < r < 1:

1/(n+1) < r ≤ 1/n

a^r – 1 ≤ a^1/n – 1 < (a-1)/n = (n+1)/n ⋅ (a-1) ⋅ 1/(n+1), (n+1)/n = 1ⁿ+1/n ≤ 2

(a-1)/n < 2⋅(a-1)⋅r

-1 < r < 0:

0 < -r < 1

0 < 1 – a^r = 1 – a^r = 1 – 1/a^-r = (a^-r – 1)/a^-r < a^-r – 1 < 2⋅(a-1)⋅(-r)

0 < 1 – a^r < a^-r – 1 < 2⋅(a-1)⋅(-r)

|r| < 1 ==> |a^r – 1| ≤ 2⋅(a-1)⋅|r|

Неравенство Бернулли

a > 1, a^r/`

c ϵ ℚ

r,p ϵ ℚ, r,p < c

|r - p| < 1,

|a^r - a^p| = a^p⋅|a^r-p - 1| < a^c⋅|a^r-p - 1| ≤ a^c⋅2⋅(a-1)⋅|r-p| = M_c⋅|r-p|, M_c = a^c⋅2⋅(a-1)

ax, x notϵ ℚ, c > x, c ϵ ℚ. r_n ϵ ℚ, r_n → x, r_n < c

∃ lim_n→∞a^rn = a^x

Доказательство:

r_n, r_m

∃ N : |r_n - r_m| < 1 для n,m > N

|a^rn - a^rm| < M_c⋅|r_n - r_m| < M_c⋅(ℰ/M_c) = ℰ ==> критерий Коши доказан, предел существует

r_n → x, p_n → x

0 ≤ |a^rn - a^pn| < M_c⋅|r_n - p_n| → 0

|a^rn -a^x| < M_c⋅|r_n - x| ==> справедливо как для ℚ, так и для иррац.

|a^x - a^y| c > x,y, c ϵ ℚ, r_n ϵ ℚ r_n → x, r_n < c

p_n ϵ ℚ p_n → y, p_n < c

|a^rn - a^pn| < M_c⋅|r_n - p_n|

lim_x→y a^x = a^y

x < y ==> a^x < a^y

a^x = lim_n→∞ a^rn, r_n → x, r_n ϵ ℚ

a^y = lim_n→∞ a^pn, p_n → x, p_n ϵ ℚ

∃ N : n > N ==> r_n < p_n ==> a^rn < a^pn

↓ ↓

a^x ≤ a^y

x < λ < μ < y, λ,μ ϵ ℚ

r_n > λ , p_n > μ ,

a^rn < a^λ < a^μ < a^pn

ax ≤ aλ < aμ

ay ≤ aλ < aμ

ax < ay

a^x⋅a^y = a^x+y:

r_n → x, p_n → y

a^rn⋅a^pn = a^rn+pn → a^x⋅a^y = a^x+y

x_n → ∞ a^xn → +∞ lim a^x = +∞

[x_n] → ∞ a^xn ≥ [a^xn] → ∞

lim_x→–∞ a^x= 0

(a^x)^y = a^xy:

x < 0:

0 < b < 1, b = 1/a, a > 1

b^y = (1/a)^y = 1/a^y

x,y, ϵ ℕ:

y = m

(a^x)^m = a^x⋅a^x⋅…⋅a^x = a^x⋅m

y < 0:

–m > 0

(a^x)^m = 1/a^x(–m) = 1/a^-xm = a^xm

y = 1/n:

(a^x)^1/n = ⁿ√a^x

(a^x/n)ⁿ = a^(x/n)⋅n = a^x ==> a^x/n = ⁿ√a^x = (a^x)^1/n

(ax)1/n = ax/n

y = m/n:

(a^x)^m/n = ((a^x)^1/n)^m = (a^x/n)^m = a^(x/n)⋅m = a^x⋅(m/n)

p_n → y, p_n ϵ ℚ:

(a^x)^pn = a^x⋅pn

x⋅pn → x⋅y

(a^x)^pn → (a^x)^y = a^x⋅pn → a^x⋅y

log_ax, x^α

a > 1: 0 < a < 1: a = 1:

a^x

a^x 1 log_ax 1 a^x

1. 1

log_a (xy) = log_a x = log_a y:

aα = aβ ==> α = β

a^{loga (xy)} = x⋅y:

a^{loga x + loga y} = a^{loga x} ⋅ a^{loga y} = x⋅y

log_a x = log_b x/log_b a;

log₁x

a = e = lim (1+1/n)ⁿ

e ^x = exp(x)

log_e x = ln x

x^α :

α = m/n:

x^m/n = (x^1/n)^m .

x^α = e ^{α⋅ln x} , x > 0

x^α – непрерывная функция, т.к. e ^y – непрерывная.

(x⋅y)^α = x^α ⋅ y^α :

(x⋅y)^α = e ^{α⋅ln (xy)} = e ^{α⋅ln x} ⋅ e ^{α⋅ln y} = x^α ⋅ y^α

x^α = e ^{α⋅ln x} = a^{α⋅log a x}