
Математический анализ (Белоносов В.С.)
книжка Никольского – Матан
задачник Демидовича
Высказывание – повествовательное предложение, которое может быть либо истинным, либо ложным. Пример: сейчас 9 часов 2 минуты.
Правила высказываний:
A, B – высказывание
A˄B (A и B) – истинно, когда оба истинны (конъюнкция)
A˅B (A или B) — истинно, когда хотя бы одно из них истинно (дизъюнкция)
¬A (не A) – истинно, когда A ложно (отрицание)
A=>B (A следовательно B) – ложно, когда первое истинно и второе ложно, в остальных случаях истинно (импликация)
A<=>B (A эквивалентно B) – истинно, когда оба высказывания имеют одинаковые значения, доказать: [A=>B ˄ B=>A] = [A<=>B] (эквивалентность)
Кванторы:
∀ – всеобщность (для всех, для каждого, for All)
∃ – существование (существует, найдётся, есть такой, Exist)
: или | – (такой/такие, что)
МНОЖЕСТВА
Задать множество – указать все элементы ему принадлежащие
x ϵ A – множество А включает элемент x
Ø – пустое множество, не содержащее ни одного элемента, является подмножеством любого другого.
A c B – A есть подмножество множества B [x ϵ A => x ϵ B]
A = B – два множества явл. равными, состоят из одних и тех же элементов, доказательство:
[(A c B) ˄ (B c A)] = [(x ϵ A => x ϵ B) ˄ (x ϵ B => x ϵ A)]
Объединение
A ∪ B – объединение двух множеств, элемент принадлежит объединению тогда и только тогда, когда он принадлежит хотя бы одному из объединенных множеств.
A ∪ A = A
A ∪ Ø = A
Пересечение
A ∩ B – общая часть двух множеств, элемент принадлежит пересечению тогда и только тогда, когда он принадлежит одновременно обоим множествам.
A ∩ A = A
A ∩ Ø = Ø
Разность
A \ B – исключение из множества A множества B, элемент принадлежит разности тогда и только тогда, когда он принадлежит A и не принадлежит B.
A \ A = Ø
A \ Ø = A
Дистрибутивный закон
Пусть имеются три множества A, B, C.
(A ∪ B) ∩ C = (A ∪ C) ∪ (B ∪ C) (1)
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C) (2)
(A \ B) ∩ C = (A ∩ C) \ B (3)
Доказательство (1):
1. x ϵ (A ∪ B) ∩ C ==> (x ϵ A ∪ B)∩(x ϵ C) ==> [(x ϵ A)∪(x ϵ B)]∩(x ϵ C) ==>
==> [(x ϵ A)∩(x ϵ C)] ∪ [(x ϵ B)∩(x ϵ C)] = [x ϵ A ∩ C] ∪ [x ϵ B ∩ C] ==>
==> x ϵ (A ∩ C) ∪ (B ∩ C).
2. x ϵ (A ∩ C)∪(B ∩ C) ==> … ==> x ϵ (A ∪ B) ∩ C.
Доказательство (3):
1. x ϵ (A \ B) ∩ C ==> [x ϵ A\B] ∩ [x ϵ C] ==> [x ϵ A] ∩ [x notϵ B] ∩ [x ϵ C] ==>
==> [x ϵ A∩C] ∩ [x notϵ B] ==> x ϵ (A ∩ C) \ B.
2. x ϵ (A ∩ C) \ B ==> … ==> x ϵ (A \ B) ∩ C.
x ϵ ((A\B)∩C) = x ϵ (A∩C)\(B∩C)
Дополнение к B до AB c A, A\B = CAB
Закон двойственности:
Пусть имеются два множества B,D c A. Тогда
1. CA (B^D) = (CAB)v(CAD);
2. CA(BvD) = (CAB)^(CAD).
Доказательство (1):
x ϵ CA(BD) ==> (x ϵ A) ^ (x notϵ BD) ==> (x ϵ A) ^ [(x notϵ B) v (x notϵ D)] ==>
==> [(x ϵ A)^(x notϵ B)] v [(x ϵ A)^(x notϵ D)] ==> [x ϵ CAB] v [x ϵ CAD] ==>
==> x ϵ (CAB)v(CAD)
Доказательство (2): сами.
Λ λ – лямбды
{Aλ}λϵΛ – семейство множеств А с индексом лямбда.
An = множество всех натуральных чисел, кратных n.



Aλ Aλ – семейство множеств, проецируемых в лямбду.








 λ (P,r)
= λ, Aλ=A(P,r)
λ (P,r)
= λ, Aλ=A(P,r)

A = UλeΛ Aλ = {x : ∃ λ ϵ Λ | x ϵ Aλ}
Отображение множеств
A,B – произвольные множества
отображения из A в B (A→B)
Отображения – сопоставление чисел с днями недели, человеков с фамилиями, студентов со стульями и т. д.
A –F→ B
F: A → B
F: x → y
F(x) = y,
y – образ элемена x
x – прообраз элемента y
Те элементы х, для которых есть образ у, называются областью определения (ОМЕГА)
Те элементы у, для которых есть прообраз х, называются областью значения (ДЕЛЬТА)
х ϵ ΩF <=> ∃ y ϵ B: F(x) = y
y ϵ ΔF <=> ∃ x ϵ A: y = F(x)
Пусть D с A. Рассмотрим совокупность образов всех элементов D. Это образ множества D при отображении F.
F[D] = {y ϵ B : ∃ x ϵ D | y = F(x)}
Пусть Е с В. Прообразом множества D отображения F явл. Множество всех элементов множества E. Это полный прообраз.
F-1[E] = {x ϵ A : F(x) ϵ E}
Совокупность всех х, таких, что F(x) = y.
F-1[y]
Если множество Е и область определения не пересекаются, то полный прообраз множества Е есть пустое множество.
F-1[E] = 0
D1,D2 c A
F[D1 v D2] = F[D1] v F[D2]
F[D1 ^ D2] c F[D1] ^ F[D2]
E1,E2 c B
F-1[E1v E2] = F-1[E1] v F-1[E2]
F-1[E1^ E2] = F-1[E1] ^ F-1[E2]
x ϵ F-1[E1v E2] <=> F(x) ϵ E1v E2 <=> F(x) ϵ E1 v F(x) ϵ E2 <=> (x ϵ F-1[E1])v (x ϵ F-1[E2]) <=>
<=> x ϵ F-1[E1]v F-1[E ].
A,B,C
F: A → B, G: B → C.
x ϵ ΩF ; y = F(x), y ϵ ΩG ; z = G(y).
Суперпозиция (композиция) GoF
z = G(y) = G(F(x))
(GoF)(x) = G(F(x))
ΩgoF = F-1[ΩG]
x e ΩGoF <=> F(x) e ΩG <=> x e F-1[ΩG]
ΔF = ??? []
Взаимное отображение
Отображение называется взаимно однозначным, если для всех элем области B прообраз состоит не более, чем из одного элемента, т. е. y=F(x) имеет единственное решение.
∀ y ϵ B : F-1[y]
∀ y ϵ ΔF : F-1[y]
(F(x1) = y) ^ (F(x2) = y → x1=x2
F(x1) = F(x2) ↔ x1=x2
Пусть имеется взаимно однозначное отображение F: A ↔ B. Тогда ∀ y ϵ ΔF ∃! x ϵ ΩF : y = F(x).
y –F-1–> x. x = F-1(y), x – значение обратного отображения на элемент у.
x ϵ ΩF , F-1(F(x)) = x; y ϵ ΔF , F(F-1(y)) = y
Множесво А отображается в множество B, если область значений А совпадает со всем множеством B.
F: A в B ΩF = A
Множество А отображается на множство В, если область определений А совпадает с множеством Вю
F: A на B ΔF = B
В гости к одному человеку пришло бесконечное количество гостей. Каждый из них приел в шляпе и повесил её на вешалку. Уходя, первый гость надел шляпу второго. Второй – третьего, и так далее. В итоге каждый гость ушёл в шляпе, а одна осталась у хозяина.
Множества равномощные, если существет взаимно однозначное отображение одного на другое.
F: A на B
F-1: B на A
Отобразить все натуральные числа на чётные:
k → 2k
Отобразить все натуральные числа на нечётные:
k → 2k – 1
Пусть A,B,C – множества
F: A → C
G: B → C => G-1: C → B
G-1o F: A → B
Множество A более мощное, чем B, если A и B не эквивалентны и множество B эквивалентно С : СсA
Какое бы множество мы не взяли, если мы рассмотрим множество всех его подмножеств, то их мощность окажется больше изначального множества.
А счётно тогда и только тогда, когда существует взаимнооднозначное отображение с множеством натуральных чисел.
Свойства счётных множеств:
1. все подмножества тоже счётны;
пусть все элементы А пронумерованы а1,а2,... двигаясь по ряду, проверяем, попадает ли элемент в В, если да – присваиваем ему первый номер, потом второй и т. д.. В итоге получим бесконечное количество пронумерованных элементов множества А
2. у любого бесконечного множества есть счётное подмножество;
пусть b1,b2,b3 – элементы A. Возьмём произвольный элемент и назовём его b4. Среди оставшихся евозьмём любой произвольный снова и т.д.. Объединив все b в множество B, получим счётное B.
3. счётное семейство счётных множеств. Представим себе последовательность множеств A1,A2,A3,...,An,... каждое из которых счётно (∀ k Ak счётно) ({Ak}kϵN). Uk=1 Ak = UkϵN Ak – счётно.




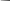

 A1 a11
a12
a13
a14
…………
A1 a11
a12
a13
a14
…………
 A2 a21
a22 a23
a24 ………… каждый
элемент стоит на какой-то диагонали,
если мы будем
A2 a21
a22 a23
a24 ………… каждый
элемент стоит на какой-то диагонали,
если мы будем
A3 a31 a32 a33 a34 ………… двигаться по схеме, давая номера, то пронумеруем все
 ……………………………… элементы.
……………………………… элементы.
………………………………
4. пусть есть два счётных множества A,B. Тогда декартово произведение AxB тоже счётно. Из последовательности a1,a2,a3,... и b1,b2,b3,... возьмём (am,bn). Декартово произведение есть упорядоченные пары произвольного элемента из А с произвольным элементом из В. AxB = {(am,bn)}m,n=1

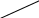



 (a1,b1)
(a1,b2) (a1,b3) …………
(a1,b1)
(a1,b2) (a1,b3) …………
(a2,b1) (a2,b2) (a2,b3) …………
(a3,b1) (a3,b2) (a3,b3) …………
5. множество всех десятичных дробей несчётно. Пусть 0,α1,α2,α3, … – десятичные дроби.
α1 = α11 α12 α13 α14 …………
α2 = α21 α22 α23 α24 …………
α3 = α31 α32 α33 α34 …………
……………………………….
……………………………….
Действительные числа
Аксиомы сложения, умножения, сравнения действительных чисел для ∀ a,b,c ϵ Q:
1. ∃! a+b: m/n + p/q = (mq+np)/nq ;
2. a + b = b + a ;
3. (a + b) + c = a + (b + c) = a + b + c ;
4. a + 0 = a ;
5. ∃! (-a) : a + (-a) = 0 , a + (-b) = a – b ;
6. ∃! a∙b ;
7. a∙b = b∙a ;
8. (a∙b)∙c = a∙(b∙c) ;
9. a∙1 = a ;
10. ∃! a-1 ≠ 0 : a∙a-1 = 1 ;
11. a∙(b+c) = a∙b + a∙c ;
12. 0 ≠ 1 ;
13. либо a > b, либо a < b, либо a = b ;
14. a < b, b < c => a < c ;
15. a < b => a+c < a+b ;
16. a < b, c > 0 => ac < bc ;
17. ∀ a ϵ Q ∃ n ϵ N : a < n (аксиома Архимеда).
Всякое поле, в котором выполняется аксиома Архимеда, называется упорядоченным архимедовым полем.
Док., что a(-b) = -ab:
0 = a⋅0,
0 = a(b + (-b)) = ab + a(-b),
a(-b) = -ab. Чтд.
[] <ДОМАШКА>
Док., что:
∀ a ≠ 0 a⋅a>0
a > 0 => a-1 > 0
a < 0 => a-1 < 0
a < 0, b < 0 => ab > 0
1 > 0
[] </ДОМАШКА>
Следствие 1:
a ϵ Q, ∀ n ϵ N a < (1/n = n-1) ==> a ≤ 0.
if a > 0 then 1/a > 0. ∃ m ϵ N :
1/a < m,
1 < am,
1/m < a – false (a < n-1) => a ≤ 0
Следствие 2:
a ϵ Q, A > 1
∀ n ϵ N a < A-n ==> a ≤ 0.
If A-n = 1/An = 1/A⋅A⋅A⋅...⋅A
A > 1 => A = 1+b, b > 0;
An = Σk=0n cnkbk > cn1b1 = nb,
An = (1+b)n > nb,
1/An < 1/nb => A-n < 1/nb => a < 1/nb => ab < 1/n => ab ≤ 0 => a ≤ 0
a |a| = (a, a ≥ 0) OR (-a, a ≤ 0)
∀ a,b ϵ Q |a+b| ≤ |a| + |b| (неравенство треугольника)
| |a| - |b| | ≤ |a – b|
Рациональные числа
m/n ↔ (m,n) ϵ Z×N
(Декартово произведение целых и натуральных чисел даёт множество всех пар рациональных чисел)
Десятичное представление рациональных чисел:
α0,α1α2...αn = α0 + α1α2...αn/10n
Дробь можно перевести в десятичную, если знаменатель можно представить в виде 2n5m.
⅓ = 0,333333333...
1/9 = 0,111111111...
½ = 0,500000000...
α0 ≤ a < α0 + 1, α ϵ N, a ϵ Q.
α0 – целая часть числа a,
α0,α1 ≤ a < α0,α1 + 0,1
α1 – десятая часть a,
α0,α1,α2 ≤ a < α0,α1,α2 + 0,01
α2 – сотая часть a,
. . .
α0,α1...αn ≤ a < α0,α1...αn + 10-n
a = p/q
α0,α1...αn ≤ p/q < α0,α1...αn + 10-n;
α0,α1...αn ⋅q ≤ p⋅10n < α0,α1...αn ⋅q + q
0 ≤ p⋅10n - α0,α1...αn⋅q < q
qn+1 = p⋅10n+1 - α0,α1...αnαn+1⋅q = p⋅10n+1 – α0α1...αn⋅10⋅q – αn+1⋅q = 10 [10np – α0α1...αn⋅q] – αn+1q;
qn+1 = 10⋅qn – αn+1⋅q
10qn = αn+1⋅q + qn+1
0 ≤ qn+1 < q
10qn+1 = αn+2⋅q + qn+2
qk = qk+t
10⋅qk = αk+1⋅q + qk+1
10⋅qk+t = αk+t+1⋅q + qk+t+1
αn = αn+t , n > k.
FUCK THAT SHIT
x = 0,α1α2...αn
10nx = α1α2...αn,α1α2...αn = α1α2...αn + 0,α1α2...αn = α1α2...αn + x;
x = (α1α2...αn)/(10n-1), т. е. целое число разделить на n девяток.
α0,α1...αk αkn...αk+t = α0,α1...αk + 0,01...0k αkn...αk+t = α0,α1...αk + 10-k⋅0,(k)/(αk+1-αk+t ) =
= α0 + (α1...αk)/10k + ( (1/10k) ⋅ ((αk+1-αk+t )/(10t-1)) )
Подобрать обыкновенную дробь, равную:
1) 0,222...
2) 0,444...
3) 0,555...
4) 0,666...
5) 0,777...
6) 0,888...
a > b <=> ∃ k ≥ 0 : α0 = β0, α1 = β1, …, αk-1 = βk-1, αk > βk,
x2 = 2 ; x = m/n – несократимая дробь;
m2/n2 = 2
m2 = 2n2 => m = 2p => 4p2 = 2n2 => 2p2 = n2 => n = 2q.
Значит, m/n = 2p/2q (сократима) – противоречие.
Бесконечная непериодическая дробь – иррациональное.
рациональные U иррациональные = действительные, вещественные.
ПАНКИ ХОЙ!
Лемма о плотности:
1. Плотность – между любыми двумя действительными числами a и b лежит бесконечное количество действительных (рац. и нерац.) чисел c таких, что a < c < b.
2. a > b, если a = a0,a1,a2,...,an, a > 0,
b = b0,b1,b2,...,bn, b > 0,
ai = bi, i = (1...m),
am+1 > bm+1 .
Грани
Верхних/нижних граней может быть бесконечно много, и среди них есть только одна точная верхняя/нижняя грань.
Теорема о существовании точной грани: всякое непустое, ограниченное сверху/снизу множество вещественных чисел имеет точную верхнюю/нижнюю грань.
«Весь анализ стоит на грани».
Доказать существование точной верхней (нижней) грани.
Арифметические действия с вещественными числами
Лемма о единственности:
Пусть даны два вещественных числа a и b. Если для любого рационального числа e>0 числа a и b могут быть заключены между одними и теми же рациональными границами s и s' : s ≤ a ≤ s', s ≤ b ≤ s', разность между которыми s' – s можно сделать меньше e, то числа a и b необходимо равны (a = b).
Доказательство:
Предположим, a < b. Тогда между этими двумя числами можно вставить два рациональных числа a < r < r1 < b, то s < r < r1 < s' => s – s' > r1 – r > 0, то есть мы не можем сделать разность s' – s сколь угодно малой, что противоречит условию.
Определение:
Пусть даны два вещественных числа α,β. Их суммой α + β = γ назовём такое вещественное число, что a + b < γ < a' + b' , такие, что a < α < a', b < β < b' , причём a' – a = e , b' – b = e.
Произведение вещественных чисел
a < α < a', b < β < b', существует такое вещественное число γ=αβ, что ab < γ < a'b'.
1. γ = sup{ab}, ab < a'b'. α < a0' , β < b0', a'<a0', b' < b0',
2. a'b' – ab = a'(b'–b) + b(a'–a) <= (a0'+b0')((b'–b) + (a'–a)).
Определение предела последовательности
Определение предела последовательности на языке неравенств.
Число а называется пределом последовательности xn, ЙЭЭсли для любого ℰ > 0 существует такой номер N, что при всех n > N выполняется неравенство |xn – a| < ℰ.
Число а называется пределом последовательности xn, ЙЭЭсли для любого ℰ > 0 все числа (точки) xn принадлежат интервалу (a–ℰ, a+ℰ) при n > N.
a – ℰ < xn < a + ℰ
a = lim xn xn → a
Последовательность имеет предел, если она сходящаяся.
Любой интервал (c,d), содержащий а, называется окрестностью точки а.
ААпределЕЕЕние на языке окрестностей
Точка а называется пределом последовательности xn, ЙЭЭсли вне любой окрестности точки а содержится конечное или пустое множество точек последовательности.
Последовательность сохраняет знак с некоторого N.
Определение
Говорят, что xn → ∞, n → ∞, если для любого Е > 0 ∃ N : xn > E ∀ n > N.
Любой интервал (M, ∞) является окрестностью бесконечности.
Пусть последовательность имеет два предела a, b, a < b, т. е. а = lim xn, b = lim xn. Возьмём ℰ = (b–a)/4. Тогда в окрестностях (a–ℰ, a+ℰ), (b–ℰ, b+ℰ) конечное количество точек; a+ℰ > b–ℰ если они не пересекаются; a+ℰ < b–ℰ если они пересекаются.
∀ ℰ > 0 ∃ N : |xn – a| < ℰ ∀ n > N
|xn| > |a|/2.
ℰ = |a|/2 ≠ 0 |a| – |xn| ≤ |xn – a| < |a|/2
Теорема (переход к пределам в неравенствах)
Если xn→ a, yn→ b и ∀ n xn ≤ yn , то a ≤ b.
Арифметические свойства последовательностей:
lim xn/yn = lim xn / lim yn, lim yn ≠ 0
lim xn = a, lim yn = b : b ≠ 0
xn/yn – a/b = (xn – a)/yn – a(yn – b)/ynb
∃ N1 : |yn| > |b|/2 (∀ n > N1)
|xn/yn – a/b| < (2|xn–a|) / |b| + |yn–b| (2|a|) / b2 (∀ n > N2)
∀ ℰ>0 ∃ N2 : |xn–a|<ℰ (∀ n > N2)
N = max(N1,N2,N3)
|xn/yn – a/b| < ℰ1 (∀ n > N) => ℰ1 = 2ℰ/|b| + (2ℰ|a|)/b2
|xn/yn – a/b| < 2ℰ/|b| + (2ℰ|a|)/b2 (∀ n > N), правая часть может быть сколь угодно малой, но больше нуля.
Определение:
Переменная величина xn называется бесконечно малой, ЙЭЭСЛИ при n→∞lim xn = 0, т. е.
∀ ℰ>0 ∃ N : |xn|<ℰ ∀ n > N.
Переменная величина yn называется бесконечно большой, если при n→∞lim yn = ∞, т. е.
∀ E>0 ∃ N : |yn|>E ∀ n > N.
(1) |xn| ≤ M ∀ n, yn → ∞ => lim xn/yn = 0
(2) |xn| ≥ m>0 ∀ n, yn → 0, yn ≠ 0 => lim xn/yn = ∞
(3) Сумма любого конечного числа бесконечно малых величин xn, yn является бесконечно малой величиной xn+ yn.
(4) Произведение ограниченной переменной xn на бесконечно малую величину yn есть бесконечно малая величина xnyn.
Последовательность x1,x2,...,xn называется монотонно убывающей (невозрастающей), если xn+1 ≥ xn.
Последовательность x1,x2,...,xn называется монотонно возрастающей (неубывающей), если xn+1 ≤ xn.
Теорема (о существовани предела у монотонной последовательности):
Пусть дана неубывающая (монотонно возрастающая) последовательность. Если она ограничена сверху, то она необходимо имеет конечный предел. Иначе xn → +∞.
Пусть дана невозрастающая (монотонно убывающая) последовательность. Если она ограничена снизу, то она необходимо имеет конечный предел. Иначе xn → –∞.
a = sup{xn} :
1) a ≥ xn ∀ n
2) ∀ ℰ>0 ∃ N : xn>a–ℰ
Любое иррациональное число есть предел последовательности рациональных чисел.
rn → α, α>0
rn = α0,α1α2...αn
Число e
yn+m – yn = 1/(n+1)! + 1/(n+2)! + … + 1/(n+m)! = 1/(n+m)! ⋅ (1 + 1/(n+2) + 1/(n+2)(n+3) + … + 1/(n+2)..(n+m)) < 1/(n+1)! ⋅ (n+2)/(n+1)
(n+2)/(n+1)2 < 1/n
limm yn+m = e => 0 < e – ym < 1/(n!⋅n)
z = (e – yn)(n!⋅n)
0 < z < 1
z < zn
e = ym + z/(n!⋅n)
n = 5: z/(n!⋅n) < 1/(1⋅2⋅3⋅4⋅5⋅5) = 1/600
0 < e – y5 < 1/600;
n = 5: z/(n!⋅n) < 1/(1⋅2⋅3⋅4⋅5⋅6⋅6) = 1/4320
0 < e – y6 < 1/4320.
Критерий Коши:
Для того, чтобы последовательность x1,x2,...,xn имела предел, необходимо и достаточно, чтобы для любого ℰ > 0 сущeствовал такой номер N, что |xn – xm| < ℰ для всех n,m > N.
∀ ℰ > 0 ∃ N : |xn – xm| < ℰ ∀ n,m > N
1) xn → a
|xn – a| < ℰ/2 n>N
|xn – xm| = |xn – a – (xm– a)| <= |xn– a| + |xm– a| < ℰ/2 + ℰ/2 = ℰ n,m>N
Пусть выполнен критерий Коши. Тогда
A = {α ϵ R | ∃ N : xn > α ∀ n>N}
A' = {α' ϵ R | ∃ N : xn < α' ∀ n>N}
A U A' = O
α э A, beta < α => beta э A
xm – ℰ < xn < xm + ℰ
xm – ℰ ϵ A
xm + ℰ ϵ A'
α < α'
Пусть a = sup {α} = sup A
α ≤ a ≤ α
xm – ℰ ≤ a ≤ xm + ℰ
|xm – a| ≤ ℰ ∀ m>N ==> lim xm = a
Лемма о вложенных отрезках:
an = a1,a2,a3,...,an
bn = b1,b2,b3,...,bn
an < bn ∀ n
an+1 ≥ an ∀ n
bn+1 ≤ bn ∀ n ==> bn – an → 0 (n → ∞)
an ≤ bn ≤ b1 ==> lim an = c
bn ≥ an ≥ a1 ==> lim bn = c'
0 = lim(bn – an) = lim bn – lim an = c' – c ==> c' = c
Пусть имеется бесконечная последователность вложенных друг в друга отрезков так, что каждый последующий отрезок соержится в предыдущем, причём с возрастанием номера длины отрезков стремятся к нулю. Тогда концы отрезков an и bn стремятся к общему пределу, который является точкой, общей для всех пределов.
