Действия с линейными преобразованиями. Произведение линейного преобразования на число.
Пусть
– линейное преобразование линейного
пространства L над
полем
и k – любое число из
.
Линейное преобразование
произвольному вектору
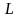ставит в соответствие единственный
вектор
.
Вектор k∙
.
Если вектору
поставить в соответствие вектор k∙
,
то имеем преобразование пространства
:
k∙
=
(
).
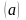Это
преобразование пространства
называют произведением преобразования
на число
и обозначают
:
( ) = ( )=
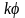Теорема 1. Если линейное преобразование линейного пространства над полем и – любое число из , то есть линейное преобразование линейного пространства .
Теорема 2.
Если
– матрица линейного преобразования
линейного пространства L
в базисе
,
то матрица линейного преобразования
в базисе
есть kA.
Пример 1.
Пусть
матрица линейного преобразования
линейного пространства
над полем
в базисе
=(
,
).
Найти матрицу преобразования 2
;
Решение.
Матрица преобразования 2
есть 2A=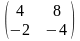
.
Сложение и вычитание линейных преобразований.
Пусть даны линейные преобразования
и
линейного пространства
.
Если
любой вектор из
,
то
=
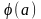и
=
‑ векторы из
.
Если вектору
поставим в соответствие единственный
вектор
из
,
то получим преобразование линейного
пространства
.
Оно называется суммой линейных
преобразований
и
и обозначается
+
.
Итак, по определению
(
+
)
=
+
=
+
.
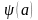Аналогично определяется разность линейных преобразований
( – ) = ‑ = ‑ ..
Теорема 3. Если и – линейные преобразования линейного пространства , то преобразования + и – линейного пространства являются линейными.
Теорема 4. Если
и
– матрицы, соответственно, линейных
преобразований
и
линейного пространства L
в базисе
,
то матрицы
+
,
–
являются соответственно матрицами
линейных преобразований
+
и
–
в том же базисе.
Пример 2. Пусть
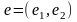базис линейного пространства
,
,
– его линейные преобразования и их
матрицы соответственно
.
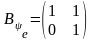Найти матрицy линейных
преобразований в базисе е:
2 +3 ;
3 – .
Решение.
1) 2A+3B=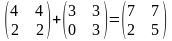
;
2) 3B–A=
.
Умножение линейных преобразований.
В линейном пространстве
даны линейные преобразования
и
.
Результат последовательного выполнения
линейных преобразований
и
является преобразованием линейного
пространства
.
Оно называется произведением
линейных преобразований
и
и обозначается
Теорема 5. Произведение линейных преобразований и линейного пространства является линейным преобразованием этого пространства.
Теорема 6. Если
и
,
соответственно, матрицы линейных
преобразований
и
линейного пространства
в базисе
,
то матрица линейного преобразования
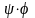линейного пространства
в базисе
есть
.
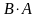Пример 3. Пусть
,
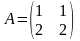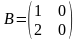матрицы линейных преобразований
соответственно
и
линейного пространства
в базисе
.
Найти матрицы преобразований в базисе
.
1) ;
2) ;
3) ( + ) ;
Решение.
1)
.
2)
.
3)
.
Свойства линейных операций над матрицами
Операции сложения матриц и умножения матрицы на число называются линейными операциями над матрицами. Непосредственно из определений вытекают следующие свойства линейных операций.
Для
любых матриц 
одинаковых
размеров и любых чисел 
справедливы
равенства:
1. 
(коммутативность
сложения);
2. 
(ассоциативность
сложения);
3. существует
нулевая матрица 
(тех
же размеров, что и 
): 
4. существует
матрица 
,
противоположная матрице 
5. 
;
6. 
;
7. 
;
8. 
.
№28
Собственные векторы и собственные значения линейного оператора
Ненулевой
вектор 
называется
собственным вектором линейного
оператора 
,
если 
(
для
комплексного 
),
такое, что 
Число 
называется
собственным числом (собственным
значением) оператора f,
соответствующим этому собственному
вектору.
Если
в некотором базисе оператор f имеет
матрицу А и
в том же базисе вектор
имеет
координатный столбец X,
то 
или 
Собственные
числа
линейного
оператора
-
корни характеристического уравнения 
,
где 
-
матрица оператора f, 
-
символ Кронекера.
Для
каждого собственного значения 
соответствующие
собственные векторы могут быть найдены
из матричного уравнения 
или
соответствующей ему системы линейных
уравнений
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
где 
-
соответствующие собственные значения.
№29
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:
(x, y) = (y, x),
(α·x, y) = α·(x, y),
(x + y, z) =(x, z) + (y, z),
(x, x)> 0 при x ≠ 0, (0, 0) = 0,
то в пространстве L определено скалярное произведение (x, y).
Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.