
- •12. Анализ цепи с последовательным соединением активного сопротивления, индуктивности и емкости
- •24. Соединение приемников трехфазной цепи треугольником.
- •29.Влияние индуктивности и емкости на форму несинусоидального тока и напряжения.
- •36.Магнитные цепи. Основные законы магнитных цепей.
- •41.Вольт-амперная характеристика катушки с ферромагнитным сердечником. Влияние немагнитного зазора на вах
- •47.Причины возникновения переходных процессов в электрических цепях. Законы коммутации.
- •50.Отключение цепи с индуктивностью от источника постоянного напряжения.
- •51.Включение r,l на синусоидальное напряжение.
- •57.Переходные процессы при включении цепей на синусоидальное напряжение.
- •64.Система уравнений электромагнитного поля в дифференциальной форме.
- •65. Система уравнений электромагнитного поля в дифференциальной форме.
- •66.Электростатическое поле. Основные задачи электростатики.
- •69. Вычисление емкости. Емкость двухпроводной линии передач.
- •71.Рассчет индуктивности двухпроводной линии.
- •75.Длинна волны. Глубина проникновения. Экранирование в переменном электромагнитном поле.
50.Отключение цепи с индуктивностью от источника постоянного напряжения.
Рассмотрим
отключение цепи R, L от источника
постоянного напряжения. Пусть в
электрической цепи (рис. 3.3) в момент
времени t=0
переключатель переключается из положения
1 в положение 2. После коммутации
электрическое состояние цепи описывается
уравнением
![]()
Характеристическое
уравнение:
![]() ,
,
корень
характеристического уравнения
![]() .
На основании (3.4) свободный ток
.
На основании (3.4) свободный ток
![]() ,
,
где
![]() – постоянная времени.
– постоянная времени.
Установившийся ток iy(t)=0, тогда согласно (3.5), переходный ток
![]() .
.
По первому закону коммутации: i(0-)=i(0+). Т.к. i(0-)=I0, где I0=U/Rк – ток в цепи до коммутации, следовательно,
![]() . (3.8)
. (3.8)
На рис. 3.4 показана зависимость переходного тока от времени при отключении R, L цепи от источника постоянного напряжения.
51.Включение r,l на синусоидальное напряжение.
u = Umsin(ωt + ψ),
то установившийся ток
iу = Um / Z sin(ωt + ψ - φ),
где:
![]() –
полное сопротивление цепи;
φ = arctg(ω
L/R) - угол сдвига фаз между напряжением
и током.
–
полное сопротивление цепи;
φ = arctg(ω
L/R) - угол сдвига фаз между напряжением
и током.
С вободный
ток определяется
вободный
ток определяется
iсв = A e-t/τ.
Суммируя установившуюся и свободную составляющие, получим выражение для переходного тока:
i = iу + iсв = Um / Z sin(ωt + ψ - φ) + A e-t/τ.
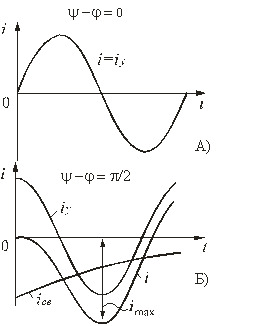 Рис.
5.7
Рис.
5.7
используя независимые начальные условия при t = 0
i(0-) = i(0+) = 0,
находим постоянную интегрирования:
A = -Um / Z sin(ψ - φ).
Тогда переходный ток:
![]() .
.
Зависимости переходного тока от времени при различных значениях разностей ψ - φ показаны на рис. 5.7. Их анализ позволяет сделать следующие выводы.
Если в момент включения установившийся ток равен нулю (ψ - φ = 0 или ψ - φ = π), то свободной составляющей тока не возникает и в цепи сразу возникает установившийся режим:
i = iу = Im sin(ωt) = Um / Z sin(ωt).
Если в момент включения установившийся ток имеет наибольшее значение (ψ - φ = π / 2), свободный ток достигает максимального по модулю значения приблизительно через половину периода, однако ни при каких условиях он не может превышать удвоенной амплитуды установившегося тока (рис. 5.7 б).
5 2.Переходные
процессы при включении R,C
на постоянное напряжение.
Предположим, что в момент времени
t=0 цепь, состоящая
из сопротивления R и
емкости С, включенных последовательно,
включается на постоянное напряжение U
(рис. 3.5). По второму закону Кирхгофа
2.Переходные
процессы при включении R,C
на постоянное напряжение.
Предположим, что в момент времени
t=0 цепь, состоящая
из сопротивления R и
емкости С, включенных последовательно,
включается на постоянное напряжение U
(рис. 3.5). По второму закону Кирхгофа
uR+uc=U.
Так
как
![]() ,
,
![]() ,
уравнение будет иметь вид
,
уравнение будет иметь вид
![]() .
.
Характеристическое уравнение:
RCp+1=0
имеет
один корень
![]() .
Тогда, на основании (3.4), можно записать
выражение для свободного напряжения
на емкости
.
Тогда, на основании (3.4), можно записать
выражение для свободного напряжения
на емкости![]() ,
,
где τ=RC – постоянная времени.
Емкость не проводит
постоянный ток, поэтому в установившемся
режиме icус(t)=0
ucус(t)=U.
Тогда, согласно (3.4),![]() .
(3.9)Постоянная
интегрирования А находится из
начальных условий (второй закон
коммутации). До момента включения
конденсатор был не заряжен, поэтому при
t=0 uc=0
из (3.9) при нулевых начальных условиях
следует0=U+A,
откуда A= U.Следовательно,
.
(3.9)Постоянная
интегрирования А находится из
начальных условий (второй закон
коммутации). До момента включения
конденсатор был не заряжен, поэтому при
t=0 uc=0
из (3.9) при нулевых начальных условиях
следует0=U+A,
откуда A= U.Следовательно,![]() .
(3.10)
.
(3.10)
Ток
в цепи во время переходного процесса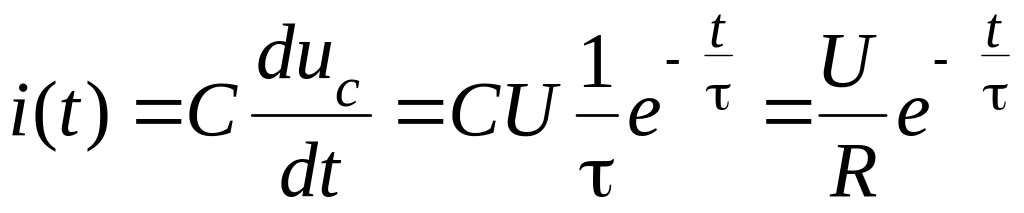 .
(3.11)
.
(3.11)
Г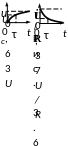 рафики
изменения напряжения и тока при включении
R, C
цепи на постоянное напряжение показаны
на рис. 3.6.
рафики
изменения напряжения и тока при включении
R, C
цепи на постоянное напряжение показаны
на рис. 3.6.
53.переходные
процессы при разрядке через сопротивление
заряженного конденсатора.
Пусть емкость, заряженная до
напряжения U, в момент
t=0 подключается к
сопротивлению R (рис.
3.7). Переходный процесс описывается
дифференциальным уравнением![]() .
.
Установившееся напряжение на емкости ucу(t)=0. Поэтому, согласно (3.4),
![]() .
(3.12)
.
(3.12)
Постоянная
А находится из второго закона
коммутации (3.2). Тогда при t=0
из (3.12) следует U=A.![]() ,
(3.13)
,
(3.13)
а переходный ток в цепи
![]() ..
(3.14)
..
(3.14)
К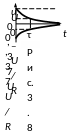 ривые
изменения напряжения и тока при разряде
емкости показаны на рис. 3.8.
ривые
изменения напряжения и тока при разряде
емкости показаны на рис. 3.8.
55.Переходные
процессы при включении цепи R,L,C
на постоянное напряжение(колебательные
процесс)Случай 1.
![]() ,
т.е.
,
т.е.
![]() (колебательный процесс).
(колебательный процесс).
Корни
характеристического уравнения комплексные
и сопряженные:![]() и
и
![]() ,
,
и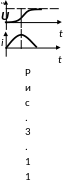 ли
ли
![]() ,
,
![]() ,
(3.25)
,
(3.25)
где
![]() .
(3.26)
.
(3.26)
Подставляем
(3.25) в (3.23) и (3.24). Произведя преобразования,
получим![]() ,
(3.27)
,
(3.27)![]() ,
(3.28)
,
(3.28)
где
![]() ;
;
![]() –
волновое сопротивление цепи.
–
волновое сопротивление цепи.
Выражения
(3.27) и (3.28) описывают затухающие колебания
с угловой частотой
![]() и коэффициентом затухания
и коэффициентом затухания![]() .
При
.
При
![]() >>
выражения(3.27) и (3.28) упрощаются:
>>
выражения(3.27) и (3.28) упрощаются:![]() ,
(3.29)
,
(3.29)![]() .
(3.30)Кривые
.
(3.30)Кривые
![]() и
i(t)
для случая
>>
приведены на рис.3.10. При этом наибольший
переходный ток в цепи
и
i(t)
для случая
>>
приведены на рис.3.10. При этом наибольший
переходный ток в цепи
![]() ,
а наибольшее переходное напряжение на
емкости
,
а наибольшее переходное напряжение на
емкости
![]() .
Длительность переходного процесса
определяется коэффициентом затухания
.
Длительность переходного процесса
определяется коэффициентом затухания
![]() .Быстрота
затухания колебаний тока определяется
его декрементом затухания – отношением
двух амплитуд, отличающихся на период,
т.е.,
.Быстрота
затухания колебаний тока определяется
его декрементом затухания – отношением
двух амплитуд, отличающихся на период,
т.е.,
где
![]() является периодом затухающих
колебаний.Н
является периодом затухающих
колебаний.Н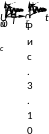 атуральный
логарифм декремента затухания
атуральный
логарифм декремента затухания
![]() называется логарифмическим декрементом
затухания.
называется логарифмическим декрементом
затухания.
56.Переходные
процессы при включении цепи R,L,C
на постоянное напряжение(апериодический
процесс и критический случай).
Случай 2.![]() ,
т.е.
,
т.е.
![]() (апериодический процесс). Согласно
(3.18) корни характеристического уравнения
p1 и p2 являются
вещественными, но различными по значению.
(апериодический процесс). Согласно
(3.18) корни характеристического уравнения
p1 и p2 являются
вещественными, но различными по значению.
Выражение
(3.24) для переходного тока в этом случае
может быть преобразовано в гиперболическую
форму:![]() .
.
На
рис. 3.11 показаны зависимости
и
![]() при
апериодическом процессе. Длительность
переходного процесса в этом случае
определяется наименьшим корнем
характеристического уравнения.Случай
3.
при
апериодическом процессе. Длительность
переходного процесса в этом случае
определяется наименьшим корнем
характеристического уравнения.Случай
3.
![]() ,
т.е.
,
т.е.
![]() (критический случай). Согласно (3.18) корни
характеристического уравнения одинаковы:
(критический случай). Согласно (3.18) корни
характеристического уравнения одинаковы:
![]() Выражения
(3.23) и (3.24) для переходного напряжения
на емкости и переменного тока в цепи
могут быть приведены к виду
Выражения
(3.23) и (3.24) для переходного напряжения
на емкости и переменного тока в цепи
могут быть приведены к виду![]() ,
,![]() .Кривые
тока i(t) и
напряжение
аналогичны
кривым, приведенным на рис. 3.11.
.Кривые
тока i(t) и
напряжение
аналогичны
кривым, приведенным на рис. 3.11.
