1.Электрическая цепь. электрический ток и напряжение. Эл. Цепь это совокупность устр-в и эл-в, предназн. Для получения и преобр. Эл. Энергии. Преобразование электрической энергии осущ. При протек. Эл. Тока. Эл. Ток – упорядоченное движение заряженных частиц. Для количественной оценки вводят силу тока. i=dq\dt – заряд проходит через нек. Поверхн. В единицу времени. Важное значение имеет направление тока. за направление тока выбирается движение положительных зарядов. Напряжение на участке цепи – разность потенциалов между крайними точками участка цепи.u=f1-f2. Напряжение на участке цепи равно работе кулоновских сил по перемещению единичного положительного заряда на участке цепи.

2.Идеализированные элементы электрических цепей – сопротивление, емкость, индуктивность. В схемах замещения используются идеализированные элементы. Эти элементы делят на пассивн. И актив. Пасс.- элементы напряжение на которых сущ. Только при протекании эл. Тока в них. Актив.- источники электр. Энергии. СОПРОТИВЛЕНИЕ. – идеал. Эл-т. Приближенно заменяет резистор в котором протекает необратимый процесс преобразования. Эл. Энергии в тепло. Под термином сопротивления понимают как сам идеализ. Элемент так и количественные оценки(для всех).R=U\i;R=ρ*l\s;G=1\R(проводимость.(сименс(см))). ИНДУКТИВНОСТЬ. Идеализир. Элемент приближенно заменяющий катушку индуктивности, в которой может накапливаться энергия м.п. U=L*di\dt(Гн).ЕМКОСТЬ.Ид.эл-т.замен.конденсатор.в кот. Может накапливаться энергия эл-го поля. C=q\u(farad). I=Cdu\dt; U=1\C∫idt.

3.Задача анализа электрических цепей. Законы кирхгофа. Осн. Топологические понятия теории эл.цепи: схема эл. Цепи – показывает соединение элементов электр. Цепи с помощью уловных графических символов., без их относительного положения в пр-ве. Ветвь – участок электрической цепи, обтекаемый одним и темже током. Узел – место соединения 3-х и более ветвей. Контур – любой замкнутый путь в электрической цепи проходящий, через последовательность нескольких ветвей и узлов, при этом каждая ветвь должна обходится не более 1 раза. Независимый контур – это контур в который входит хотябы 1 нов. Ветвь. 2-х полюсник – часть электрической цепи с двумя выводами, зажимами, полюсами. Линейные электрические цепи – эл-я цепь называется линейной если все элементы этой цепи – линейны, если хотябы один элемент нелинеен то цепь нелинейна.Задача анализа: необходимо в данной схеме найти параметры всех пассивных элементов, направления и величины всех источников э.д.с. и тока. необходимо рассчитать токи во всех ветвях эл-й цепи.Законы кирхгофа: 1.- алгебраическая сумма мгновенных значений сил тока сходящихся в узле равна 0.(в узлах эл. Цепи заряд не накапливается. 2- алгебраическая сумма напряжений на пассивных элементых любого контура цепи равна алгебраической сумме мгн-х значений э.д.с. действующих в этом контуре.

4.Применение законов к. для анализа цепей.1)произвольно выбир. Положительное направление тока в ветви.2)сост для н-1 ветвей ур-е по 2-му з.К,4) решая полученную систему относительно неизв токов. Если в результате расчета какойто тока оказался отрицательным. Это означает, что его действительное направление противоположно условно положительному.1.I1-I3-I5=0 2..(R1+R2)*I1+R5*I5=E1+E5. 3. –R5I5+(R3+R4)I3=-E5-E3.Решив систему можно настии токи

6.Метод контурных токов. Следует из законов кирхгофа и принципа наложения, этот метод позволяет уменьшить число решаемых уравнений по сравнению с методом основ. На зак-х Кирхгофа. В м.к.т. – число уравнений равно числу уравнений, которое можно составить для данной цепи по 2 закону кирхгофа. М.к.т предполагает, что в кажд. Независ. Контуре протекает свой контурный ток, в результате расчета находится токи в ветвях, через контурные токи.Токи в ветвях связ. След. Соотношением: I1=I11; I3=I22; I5=I11-I22. Тогда система уравнений полученная по закону к. может быть заменена: 1..(R1+R2)*I11+R5*(I11-I22)=E1+E5. 2. –R5I11+(R3+R4+R5)I3=-E5-E3.

7.Метод эквивалентного генератора. мостовая схема. Часто требуется рассчитать ток в одной ветви. Остальная эл-я цепь может быть представлена в виде активного двухполюсника.

В свою очередь активный двухполюсник можно представить в виде 2-х элементов. Получившаяся электрическая цепть может быть рассчитана по закону О. I=Eэкв.\R+Rв. Такую замену позволяет сделать теорема о эквивалентном источнике Е (генератора). Ток в любой ветви ав линейной эл-й цепи на изменится если подключаемая к выводу ветви ав цепь заменить эквивалентным источником(генератором). Еэк которого равна напряжению на выводах ветви ав при разомкнутой ветви ав (напряжение холостого хода) а внутреннее сопр Rв входному сопротивлению пассивной электрической цепи ав. 1)размыкают ветвь ав и известными методами определяют напряжение холостого хода на разомкнутой ветви. 2. Удаляют из схемы все ист Е оставляя их внутренне сопротивление. Мостовая схема: Найти I5.

Размыкаем ав

Uxx= -R1I1+R2I2=E\(R1R2 +R4) - R1*E\(R1+R3)

Uxx= E(R2R3-R1R4)\(R1+R3)(R2+R4). Удаляем из схемы Е

Rвх=Rab=R1*R3\(R1+R3) +R2R4\(R2+R4); Eэк=Uxx Rb=R; I5=E\R5+Rb = E*(R2R3-R1R4)\(R1+R3(R2+R4)(R5+R1R3\(R1+R3)+R2R4\(R2+R4)); Условие равновесия моста: I5=0 => R2R3=R1R4.

8.Энергетические соотношения в цепях постоянного тока. Из закона сохранения энергии следует уравнение баланса мощности, которое выражает то, что в электрической цепи суммарная мощность генерируемая всеми источниками равна суммарной мощности потребляемой всеми приёмниками. Для электрической цепи в которой действует только Е источника может быть записано в виде: ∑EkIk=∑IkRk

Кпд η=Pн\Pu=Ph\Pн+ΔP

Pu=EI; Pн=I^2Rн; ΔP=I^2*Rв. Режимы работы 2-х полюсников.(акт+пасс).

Делятся на: 1.Режим ХХ.2.КЗ.3 согл режим.4.номинальный. 1.Осущетвляется отключением нагрузки от акт. В этом режиме ток в нагр. =0, напряжение на зажимаех акт 2-х полюсн. Равно эдс экв генер. Uxх=Еэк.2.Короткое замыкание возникает когда сопротивление нагрузки равно 0.

R=0; Uкз=0;Iкз=Eэк\Rв. 3.согласованный режим соответсвует случаю когда мощность выделяемой на нагрузке максимальна. ΔP =max η=0.5;Rн=Rв.4.Режим работы акт.и пасс. 2-х полюсника на которые они рассчитаны заводом изготовителем.

9.Синусоидальный ток. Это периодический(мгн значение которого удовл. Условию i(t+T)=i(t) ток, зависящий от времени. Т- период- минимальное время, через которое повторяется значение периодической функции. Мгновенное значение синусоидального тока: i(t)=Im*sin(ωt+ψi); (ωt+ψi) – фаза – определяет стадию колебательного процесса. Для 2-х син-х функций времени синусоидальной частоты, можно ввести понятие сдвига фаз. U(t)=Um*sin(ωt+ψu); φ=(ωt+ψu) - (ωt+ψi); φ= ψu –ψi; φ>0 – напряжение по фазе опережает ток φ<0 – напряжение по фазе отст. От тока, φ=0 напряжение по фазе совпадает с током.

10.Представление син-х ф-й времени с помощью комплексных чисел и вращающихся векторов. Гармонические ф-и могут быть представлены различным образом: с помощью диаграмм, комплексных чисел, вращающихся векторой, амплитудных и фазовых спектров. То или иное представление зависит от решаемых задач. Представление с помощью диаграмм при анализе электрических цепей пер-го тока, приводит к громоздким тригонометрическим преобразованиям. Поэтому в элт для обеспечения расчетов предст. Син-е функции при помощи комплексных чисел.

Если рассматривают синусоидальные функции времени один частоты, то вектора соотв. Этим функциям вращаются с одинаковой частотой. Для единообразия вектора изображаются в момент времени т=0. Правила соотв: 1.Длинна вектора равна амплитуде(действ. Знач. Син-й функции). 2. Угол с осью действительных чисел – начальной фазе син-й функции времени. Совокупность векторов соотв действ. Значениям называется векторной диаграммой.

11.Сопротивление индуктивность и емкость в цепи синусоидального тока. Термин сопротивление является недостаточным в случае цепи переменного тока т.к. на величину тока оказывает влияние не только элементы где элементарная энергия преобразовывается в тепло, но и элементы в которых электрическая энергия может накапливаться в виде электрического магнитного поля емкости и индуктивности. Такие элементы называют реактивными.

12. Анализ цепи с последовательным соединением активного сопротивления, индуктивности и емкости

При последовательном соединении пассивных элементов электрической цепи( рис.3) ток i во всех элементах одинаков, а напряжения различны.

Запишем второе уравнение Кирхгофа для мгновенных значений (1), учитывая, что роль ЭДС играет напряжение источника питания u, и выразим напряжение на элементах uR, uL, uC через ток (2):u_R + u_L + u_C = iR+ Ldi/dt+ u_C = 1/C∫idt= UПредположим, что по цепи протекает синусоидальный ток:i = sinωt. (3)Тогда мгновенные напряжения на элементах:^uR ^{=Ri = Rsinωt = URsinωt , (4)u}L^{=Ldi/dt= ωLcosωt= ULsin(ωt+π/2), 5)uc = 1/C∫idt = cosωt = Ucsin(ωt-π/2). (6)}Отсюда вытекают следующие формулы для определения действующих значений напряжений на элементах:

U_R= IR, U_L=IωL=IX_L, U_C=I/ωC=IX_C, (7)где X_L=ωL- индуктивное сопротивление, X_C=1/ωC- емкостное сопротивление.Как видно из (4), (5), (6), напряжения на элементах изменяются по синусоидальному закону. Сумма нескольких синусоид также является синусоидальной величиной, поэтому для напряжения питания можно записать: u= ^. (8)Графики мгновенных значений тока и напряжений, построенные по (3), (4), (6), (8), показаны на рис. 4.

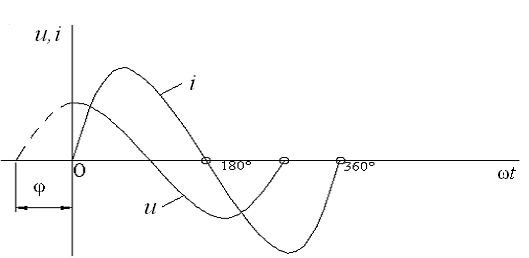
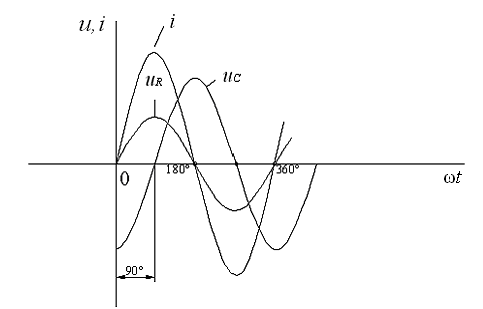
Рис.4. Графики мгновенных значений тока и напряжений для последовательной цепи.В выражении (8) для напряжения питания неизвестными величинами являются действующее значение U и сдвиг фаз φ. Наиболее легко эти величины определить из векторной диаграммы (рис.5).

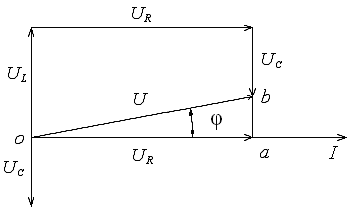
Рис.5. Векторная диаграмма для последовательной цепи при X_L > X_C Построение начинаем с вектора тока как общего для всех элементов. Затем строим векторы напряжений на сопротивлении U_R, индуктивности U_L и емкости U_C. Длины этих векторов определяются по формулам (7). Сдвиг фаз между этими векторами и вектором тока определяется из сравнения фаз тока и напряжений. Сравнивая фазы тока(3) и напряжения на сопротивлении (4), определяем, что в сопротивлении ток совпадает по фазе с напряжением. Сравнивая фазы тока (3) и напряжения на индуктивности (5), определяем, что в индуктивности ток отстает по фазе от напряжения на угол 90° или во временных единицах на четверть периода. Аналогично определяем, что в емкости ток опережает по фазе напряжение (6) на угол 90° или на четверть периода. В соответствии со вторым уравнением Кирхгофа в векторной форме вектор напряжения питания Ū равен сумме векторов напряжений на пассивных элементах: Ū= ŪR+ ŪL+ ŪC. Из диаграммы на рис. 5 можно выделить прямоугольный треугольник oab и применить к нему теорему Пифагора:^{U= =}

Из этого выражения получаем соотношение между действующими значениями тока и напряжения питания, аналогичные закону Ома:I= U/Z, (9)где ^{ž= =} . (10) Здесь ž - полное сопротивление цепи; R- активное сопротивление цепи; X- реактивное сопротивление цепи. Сдвиг фаз между током и напряжением питания φ находится из треугольника oab через тригонометрические функции: tgφ= (U_L- U_C)/UR= (X_L- X_C)/R, cosφ= R/ ž, sinφ= (X_L- X_C)/ ž. (11)

13. Анализ цепи с параллельнымсоединением Схема электрической цепи показана на рис. 8. При параллельном соединении напряжение одинаковое для всех ветвей, а токи разные. В схеме на рис. 8 активное сопротивление конденсатора принято равным нулю и учитывается только активное сопротивление индуктивной цепи( например сопротивление провода катушки индуктивности).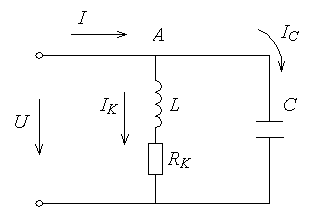

Запишем для узла А первое уравнение Кирхгофа в векторной форме:Ī= Ī_K+ Ī_C и построим векторную диаграмму, используя связи между токами и напряжениями в сопротивлении, индуктивности и емкости, установленными в разделе 3.3. Векторная диаграмма показана на рис. 9.

Рис. 9. Векторная диаграмма для цепи с параллельным соединением при Ip > IC На этой диаграммеI_C- ток в емкостной ветви;I_K- ток в индуктивной ветви;I_a- проекция вектора тока индуктивной ветви на вектор напряжения( активный ток);Ip- проекция вектора тока индуктивной ветви на ось, перпендикулярную вектору напряжения(реактивный ток);Из прямоугольного треугольника oab:^{I= ,} (12)^{где IC=U/ XC Ia= IK∙cosφk= , Ip= IK∙sinφk= .}

Сдвиг фаз между током I и напряжением U находится через тригонометрические функции:tgφ= (Ip- I_C)/ I_a; cosφ= I_a /I.В данной цепи может наблюдаться режим, называемый резонансом токов, при котором φ = 0 и I_p= I_C. В этом режиме ток I (12) минимальный I_рез = I_a , а сопротивление цепи, соответственно, максимально. Определим резонансную частоту из условия I_p= I_C: ^{= ; = ωC ;ωрез= ,}где ρ = - волновое сопротивление цепи. Если R_K много меньше ρ, то резонансная частота определяется так же, как и в последовательной цепи. Токи в ветвях I_C и I_K могут превышать потребляемый ток I, если добротность больше единицы. На рис.10 построены частотные характеристики тока I и полного сопротивления всей цепи ž=U/I

14. Законы К, в комплексной форме. Метод комплексных амплитуд расчета цепей синусоидального тока. По 1 з-ну К. для линейных значений:

∑i_k=0 => Im*∑(Im(с тчк.)* e^jωt)=0; сокращая на e^jωt получим ∑(Im(с тчк.). Алгебраическая сумма комплексов(комплексных амплитуд) токов сходящихся в узле равна 0. 2 з-н К: ∑Zk*Imr=∑Emk; алгебраическая сумма комплексов (комплексных амплитуд) равна алгебраической сумме комплексов ЭДС действующих в контуре. По форме законы О. и К. записанные для комплексов совпадают с законами О.К. записанными для переходного тока.

15.Мощность цепи синусоидального тока. В электрических цепях переменного тока протекают два различных энергетических процесса. 1 процесс связан с поступлением энергии от источников в приемник с последующим преобразованием эл-й энергии в другую. Такой энергетический процесс характеризуется активной мощностью. Другой энергетический процесс связан с поступлением энергии в приемник, накопление её в виде электрических полей связанных с реактивными сопротивлением полей и последующим возвратом в её источник. Такой энергетический процесс носит колебательных характер и носит энергетический характер. Р – активная мощность среднее значение мгновенной мощности за время равное периоду.

P=1\T ∫l0-Tl UIcosφ. Реактивная мощность определяется как Q=UIsinφ. Коэффициент мощности и его технико-экономические значения. Коэф мощности есть отношение активной мощности к полной мощности. Cosφ=P\S коэффициент мощности показывает какая доля полной мощности преобразовывается в другие виды энергии.

16. Режим резонанса. Особенности резонансного напряжения. В электрической цепи на рис.3 может быть такой режим, когда, несмотря на наличие емкости и индуктивности, ток и напряжение питания совпадают по фазе, то есть цепь ведет себя как активное сопротивление. Такой режим называется резонансом напряжений. Условия резонанса:

φ=0, tgφ=0, X_L-X_C=0, X_L=X_C.

Отсюда получаем формулу для определения частоты тока, при которой наблюдается резонанс: ^ωрез= . Режим резонанса наиболее наглядно выделяется на частотных характеристиках. Если при неизменных напряжении питания U и параметрах R, L, C изменять частоту ω, то будут изменяться индуктивное X_L и емкостное X_C сопротивления, а вслед за ними полное сопротивление ž и ток в цепи. Частотные характеристики для сопротивлений приведены на рис.6. Кривая для ž построена по (10).

Активное сопротивление можно считать неизменным, не зависящим от частоты, если пренебречь поверхностным эффектом, который заметен при высоких частотах и массивных проводниках. Индуктивное сопротивление X_L прямо пропорционально частоте, а емкостное X_C- обратно пропорционально частоте. Если частота стремиться к нулю, то XC стремится к бесконечности, а X_L─ к нулю. Вслед за X_C к бесконечности стремится полное сопротивление ž. Если частота стремится к бесконечности, то X_L стремится к бесконечности, а X_C─ к нулю. Вслед за X_L к бесконечности стремится полное сопротивление ž. При X_L=X_C( резонанс) сопротивление ž минимально и равно ž = R. При ω<ωрез X_L<X_C и сдвиг фаз носит емкостный характер( ток опережает напряжение на угол φ), при ω>ω_рез X_L >X_C и сдвиг фаз носит индуктивный характер( ток отстает по фазе от напряжения на угол φ). На рис.7 приведены частотные характеристики цепи для тока и напряжений на индуктивности и емкости. В соответствии с (9) зависимость I=f(ω) обратна зависимости ž=f(ω). При резонансе ток в цепи максимален при неизменных значениях U, R, L, C. Зависимости U_L = f(ω) и U_C = f(ω) можно построить по формулам:U_C=I X_C = X_CU/ž; U_L=IX_L= X_LU/ž.

Как видим, напряжения UL и UC тоже достигают максимального значения, но это происходит при других частотах. В режиме резонанса X_L=X_C , поэтому U_L= U_C , то есть напряжения на емкости и индуктивности равны между собой.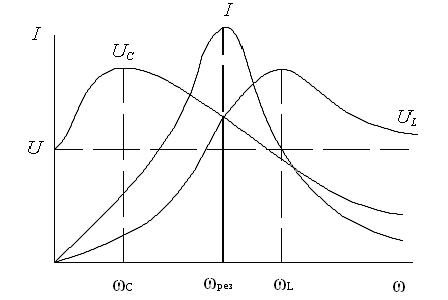

Определим индуктивное и емкостное сопротивления при резонансе:^{XLрез= XCрез= ωрезL=L = = ρ}Величина ρ зависит только от параметров цепи и называется волновым сопротивлением. Оценим величину напряжений на емкости и индуктивности в режиме резонанса:UL_рез= UC_рез= I_резXL_рез= ρU/R= UQ,где Q= ρ/R- добротность цепи.Если ρ>R, то Q>0 и UL_рез = UC_рез > U, то есть на емкости и индуктивности напряжение может значительно превышать напряжение питания.

18.Резонанс токов. Возможен в электрической цепи содержащей параллельно соединенные индуктивности и ёмкости.

В данной цепи может наблюдаться режим, называемый резонансом токов, при котором φ = 0 и I_p= I_C. В этом режиме ток I (12) минимальный I_рез = I_a , а сопротивление цепи, соответственно, максимально. Определим резонансную частоту из условия I_p= I_C:

^{= ; = ωC ;ωрез= ,}

где ρ = - волновое сопротивление цепи. Если R_K много меньше ρ, то резонансная частота определяется так же, как и в последовательной цепи. Токи в ветвях I_C и I_K могут превышать потребляемый ток I, если добротность больше единицы.

На рис.10 построены частотные характеристики тока I и полного сопротивления всей цепи ž=U/I

I(.)=YU;Y=g-jb;g-активная проводимость, b-реактивная проводимость g=1\R; b=b_L-b_C; В режиме Р. Токов на входе ток = 0, т.к. реактивная проводимость =0, полная проводимость в режиме резонанса токов будет минимальна. Следовательно сопротивление максимально. Потребляемые ток минимален.Imin=U\R=gU

19. Электрические цепи с индуктивно связанными элементами. Возникает явление взаимоиндукции. В данном контуре возникает ЭДС индукции при изменении тока в другом контуре. Явление взаимоиндукции это частный случай эл.м. индукции В качестве индуктивно свзяанных контуров как правило выступают катушки. Для расчета электрических цепей с индуктивной связанными элементами необходимо знать как ориентированы относительно друг друга.