Уравнения Эйлера для покоящейся жидкости.
Рассмотрим равновесие
жидкости (рис.11). Возьмем точку
и выделим около нее параллелепипед со
сторонами
,
,
.
Обозначим внешние силы, отнесенные к
единице массы через
.
Внешними силами здесь будут:
- объемные, пропорциональные массе параллелепипеда;
- силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.
Рассмотрим сначала силы, действующие на жидкий параллелепипед по оси X.
Проекция объемных сил
на ось X
будет равна:
;
Следовательно, проекции объемных сил на все оси:
Гидростатическое давление
в точке В обозначим
,
а в точке С - через
.
Если давление изменяется по линейному
закону и непрерывно, тогда:
;
где
- градиент гидростатического давления;
Р - давление в точке А.
Силы, действующие на грани равны:
;
Составим уравнение равновесия исследуемого нами жидкого объема относительно оси X:
Уравнение равновесия после подстановки и преобразования сможем записать в виде:
Окончательно уравнение равновесия относительно оси X будет иметь вид:
Аналогично получим уравнение равновесия относительно осей Y и Z и запишем полную систему уравнений, которые называются уравнениями Эйлера.
Впервые они были выведены в 1775 г. и выражают закон распределения гидростатического давления в дифференциальной форме.
Для дальнейшего преобразования, умножим каждое из уравнений системы на , , , соответственно
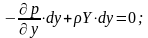
Основное уравнение гидростатики
Рассмотрим наиболее важный
для практики частный случай равновесия
жидкости, находящейся под действием
только сил тяжести. Давление на поверхности
будем считать известным и равным
,
отличным от атмосферного.
Так как на жидкость действует только сила тяжести то:
(ускорения по осям X
и Y
отсутствуют, а то оси Z,
ускорение свободного падения направлено
вниз, поэтому
).
Подставим X, Y, Z в уравнения Эйлера (первые два уравнения обращаются в нуль) и получим:
.
После интегрирования
.
Для вычисления постоянной
интегрирования С,
подставив граничные условия
и получим её значение:
а подставив С в полученное выше уравнение, запишем:
.
Уравнение выражает закон
сохранения энергии в
покоящейся жидкости.
Сумма удельной
потенциальной энергии положения Z
и удельной потенциальной энергии
давления
есть величина постоянная
во всех точках данной покоящейся
жидкости.
Распределение давления в покоящейся жидкости и газе (закон Паскаля).
.
А если учесть, что
,
то
,
где: h - глубина погружения точки в жидкости.
Это уравнение выражает закон Паскаля: давление, возникающее на граничной поверхности жидкости передается всем частицам жидкости по всем направлениям и без изменения.
Закон Паскаля используется при проектировании гидростатических машин, например, гидравлического пресса.