24. Лінійний обчислювальний процес

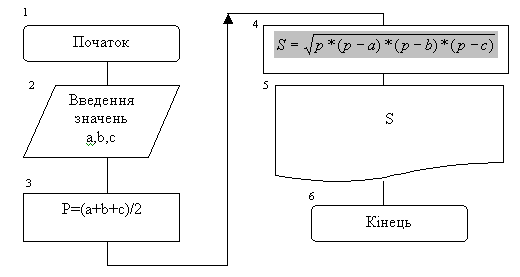
Лінійним називають такий обчислювальний процес, в алгоритмі якого використовується лише базова конструкція типу слідування. Це означає, що у процесі реалізації алгоритму лінійної структури дії виконуються один раз, а їх послідовність визначається номером блочного символу(блок із номером N завжди виконується після блоку з номером N–1, де N – натуральне число). Прикладом лінійного обчислювального процесу є обчислення площі S трикутника, якщо відомі значеннях його сторін а, b та с..

Блок-схема  алгоритму обчислення площі трикутника.

25. Розгалужений обчислювальний процес.

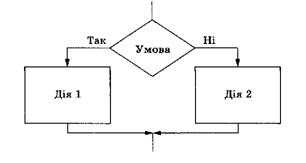
Розгалуженим називають такий обчислювальний процес, в алгоритмі якого передбачене розгалуження деякої послідовності дій на два (іноді три) напрямки залежно від результату перевірки заданої умови. В алгоритмах розгалуженої структури завжди присутній блочний символ "Вибір", після якого дії виконуються по одній із двох (трьох) гілок. Для подання розгалуженого обчислювального процесу використовується умовний оператор, схему якого наведено на рисунку:

Прикладом розгалудженого обчислювального процесу може слугувати обчислення значення наступної функції:

Блок-схема алгоритму обчислення значення y подана на рис.1.

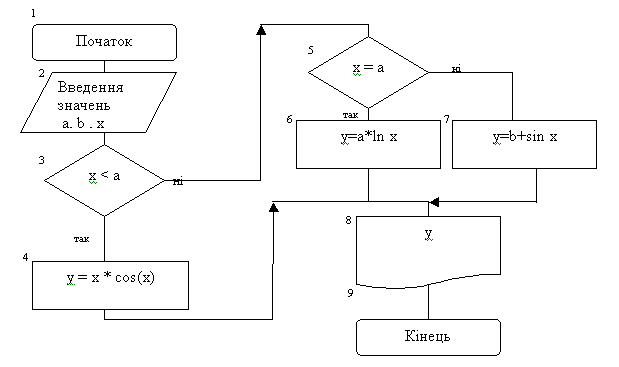
Рис.1. Схема алгоритму розгалуженої структури

26. Циклічний обчислювальний процес.

Циклічним називають такий обчислювальний процес, в алгоритмі якого деяка група блочних символів виконується багаторазово. Алгоритм циклічної структури застосовується як самостійно (наприклад, для обчислення значень функцій, для обробки масивів даних), так і в складі більш складних алгоритмів.

Для організації циклів необхідно: задати початкове значення змінної, що визначає цикл (параметр циклу), змінити цю змінну перед кожним повторенням циклу, перевірити умову продовження (закінчення) циклу. Умовою може бути: перевищення параметром циклу кінцевого значення, виконання заданого числа повторень, досягнення заданої точності обчислення.

У циклічних алгоритмах виконання деяких операторів (груп операторів) здійснюється багаторазово з тими ж або модифікованими даними.

Цикли бувають арифметичні та ітеративні. В арифметичних циклах число повторень визначається на основі зміни параметра циклу; в ітеративних циклах - цикл повторюється доти, доки не буде виконана умова виходу з циклу.

Залежно від способу організації кількості повторень циклу розрізняють три типи циклів:

1) цикл із заданою умовою закінчення роботи (ЦИКЛ - ДО);

2) цикл із зданою умовою продовження роботи (ЦИКЛ - ПОКИ);

3) цикл із заданою умовою повторень роботи (ЦИКЛ 3 ПАРАМЕТРОМ).

Прикладом циклічного обчислювального процесу є обчислення значень функції при зміні параметра х від початкового значення х₁ до кінцевого значення х₂ із кроком х₃. Один із варіантів алгоритму обчислення наведений на рис. 1.

Обчислення значень функції при зміні х від початкового до кінцевого значень із деяким кроком з виведенням величин х та y у вигляді таблиці називається табуляцією функції. В алгоритмі (рис. 1) процес безпосередньої табуляції виконується блоками 4-7. Застосування блоку "Модифікація" дозволяє зменшити кількість геометричних фігур при зображенні алгоритму циклічної структури. Варіант алгоритму табуляції функції з використанням блоку модифікації наведений на рис. 2.

Порівнявши алгоритми, наведені на рис. 1 та 2, відзначимо, що блок модифікації (третій блок на рис. 2) об`єднав у собі дії, які виконувалися блоками 3, 6 та 7 схеми рис. 1. Це зменшило кількість блоків на два, не змінивши сутності циклічного обчислювального процесу.

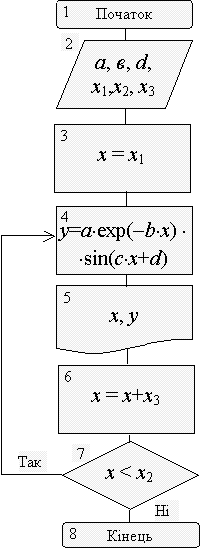
Рис. 1. Схема алгоритму циклічної структури

Рис. 2. Схема алгоритму циклічної структури з використанням блоку модифікації