
- •9. Радикальный признак Коши
- •18. Теорема Вейерштрасса
- •19. Равномерная сходимость
- •29. Вычисление р. Фурье для четных и нечетных функций
- •7. Признаки сходимости
- •14. Абсолютное условие сходимости Признаки абсолютной сходимости Признак сравнения
- •4. Знакоположительные ряды
- •26. Ряды Фурье
- •Сходимость ряда Фурье
- •1. Определение ряда
3. Геометрический ряд Так называется ряд (бесконечная сумма), члены которого образуют геометрическую прогрессию с первым членом а0 и знаменателем прогрессии, равным q.
Если |q| <
1, то существует предел суммы n первых
членов этой прогрессии при неограниченном
увеличении количества этих членов n:
![]()
В этом случае говорят о бесконечно убывающей геометрической прогрессии.
2. Числовые ряды
ЧИСЛОВОЙ РЯД –
бесконечная сумма членов бесконечной
числовой последовательности {an} называется
числовым рядом:
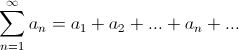 4.
Необходимые признаки сходимости ряда
4.
Необходимые признаки сходимости ряда
Теорема.
Если ряд сходится, то ![]() un=0.
un=0.
Доказательство.
Пусть ряд u1+u2+…+un… сходится,
то есть существует конечный предел ![]() =S.
Тогда имеет место также равенство
=S.
Тогда имеет место также равенство ![]() =S,
так как при n
=S,
так как при n![]() и (n-1)
. Вычитая
почленно из первого равенства
второе, получаем
и (n-1)
. Вычитая
почленно из первого равенства
второе, получаем ![]() -
=
-
= ![]() =
un=0,
что и требовалось доказать.
=
un=0,
что и требовалось доказать.
Следствие. Если ![]() un≠0,
то ряд u1+u2+…+un… расходится.
un≠0,
то ряд u1+u2+…+un… расходится.
9. Радикальный признак Коши
Снова
рассмотрим ряд ![]() с
положительными членами. Согласно
признаку Коши:
с
положительными членами. Согласно
признаку Коши:
Если ![]() ,
то ряд
сходится;
,
то ряд
сходится;
Если ![]() ,
то ряд
расходится;
,
то ряд
расходится;
Если ![]() ,
то вопрос о сходимости ряда
,
также как для признака Даламбера,
остается открытым.
,
то вопрос о сходимости ряда
,
также как для признака Даламбера,
остается открытым.
Интегральный признак Коши Пусть f (x) является непрерывной, положительной и монотонно убывающей функцией на промежутке [1, +∞). Тогда ряд
![]()
сходится, если сходится несобственный интеграл
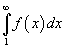 ,
и расходится, если
,
и расходится, если 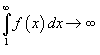 .
23.
Т-ма
Абеля
.
23.
Т-ма
Абеля
Теорема
Абеля —
результат теории степенных рядов,
названный в честь норвежского
математика Нильса
Абеля.
Пусть ![]() —
степенной ряд с комплексными коэффициентами
и радиусом сходимости
—
степенной ряд с комплексными коэффициентами
и радиусом сходимости ![]() .
.
Если
ряд ![]() является
сходящимся, тогда:
является
сходящимся, тогда:
![]() .
.
ДОКОЗАТЕЛЬСТВО
Заменой
переменных ![]() ,
можно считать
,
можно считать ![]() .
Также (необходимым подбором
.
Также (необходимым подбором ![]() )
можно предположить
)
можно предположить ![]() .
Обозначим
.
Обозначим ![]() частичные
суммы ряда
частичные
суммы ряда ![]() .
Согласно предположению
.
Согласно предположению ![]() и
нужно доказать, что
и
нужно доказать, что ![]() .
.
Рассмотрим ![]() .
Тогда (приняв
.
Тогда (приняв ![]() ):
):
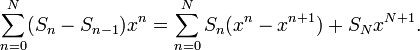
Отсюда
получается ![]() .
.
Для
произвольного ![]() существует натуральное
число
существует натуральное
число ![]() ,
что
,
что ![]() для
всех
для
всех ![]() ,
поэтому:
,
поэтому:
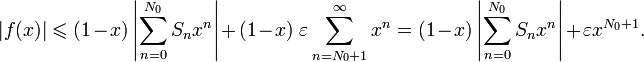
Правая
часть стремится к ![]() когда
когда ![]() пстремится
к 1, в частности она меньше
пстремится
к 1, в частности она меньше ![]() при
следовании
к
1.
при
следовании
к
1.
18. Теорема Вейерштрасса
Теорема (первая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она ограничена на нем. Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b] . Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈N найдется точка xn∈[a;b] , что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn)точек сегмента [a;b], для которых выполнено свойство f(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n... Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x0∈[a;b] : limk→∞xnk=x0 (1) Рассмотрим соответствующую последовательность (f(xnk)). С одной стороны f(xnk)>nk и поэтому limk→∞f(xnk)=+∞ (2), С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlimk→∞f(xnk)=f(x0) (3) Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д. Замечание 1 Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции. c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении функции своих граней. Замечание 2 Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)) , но функция не ограничена на этом интервале. Теорема (вторая теорема Вейерштрасса) Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения). Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой теореме Вейерштрасса c,d∈R . Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки x1,x2∈[a;b] , чтоf(x1)=c,f(x2)=d. Докажем, например, существование точки x2.
По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b]ограничена. Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем f(x)≤d−1M<d . Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.
Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c. Следствие Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок. Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.
27.
Ортогональная функция
Две
вещественные функции ![]() и
и ![]() на
интервале
на
интервале ![]() называются ортогональными,
если
называются ортогональными,
если
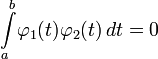
Для комплексных функций вводится комплексное сопряжение одной из функций под интегралом, для векторных — скалярное произведение функций под интегралом, а также интегрирование по отрезку заменяется на интегрирование по области соответствующей размерности.
Полезным
обобщением понятия ортогональности
является ортогональность с определённым
весом. Ортогональны с весом ![]() функции
функции ![]() и
и ![]() ,
если
,
если
![]()
где ![]() —
скалярное произведение векторов
—
скалярное произведение векторов ![]() и
и ![]() —
значений векторнозначных функций
и
в
точке
,
—
точка области
—
значений векторнозначных функций
и
в
точке
,
—
точка области ![]() ,
а
,
а ![]() —
элемент её объёма (меры).
Эта формула записана наиболее общим
способом по сравнению со всеми выше. В
случае вещественных скалярных
,
скалярное
произведение следует заменить на
обычное; в случае комплексных
скалярных
,
:
—
элемент её объёма (меры).
Эта формула записана наиболее общим
способом по сравнению со всеми выше. В
случае вещественных скалярных
,
скалярное
произведение следует заменить на
обычное; в случае комплексных
скалярных
,
: ![]() .
.
21. Радиус
сходимости степенного ряда
Так
называют радиус круга сходимости
степенного
ряда 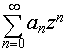 на
комплексной плоскости (или степенного
ряда
на
комплексной плоскости (или степенного
ряда 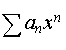 на
действительной числовой оси), т.е. такое
число r,
что ряд сходится при |z|
< r (соответственно
при |x|
< r)
и расходится при |z|
> r (соответственно
при |x|
> r).
На границе круга сходимости ряд может
как сходиться, так и расходиться.
на
действительной числовой оси), т.е. такое
число r,
что ряд сходится при |z|
< r (соответственно
при |x|
< r)
и расходится при |z|
> r (соответственно
при |x|
> r).
На границе круга сходимости ряд может
как сходиться, так и расходиться.
Для вычисления радиуса сходимости степенного ряда имеются несколько формул, например:
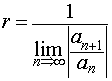 (Формула
Даламбера);
(Формула
Даламбера);
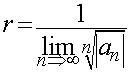 (Формула
Коши).
(Формула
Коши).
24. Ряд Тейлора и Макларена Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
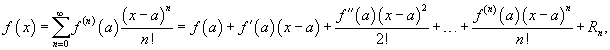
где Rn − остаточный член в форме Лагранжа определяется выражением
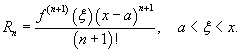
Если
приведенное разложение сходится в
некотором интервале x,
т.е. ![]() ,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
,
то оно называется рядом
Тейлора,
представляющим разложение функции f (x) в
точке a.
Если a
= 0,
то такое разложение называется рядом
Маклорена:
![]()
Разложение некоторых функций в ряд Маклорена
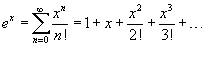
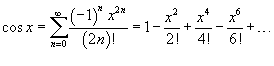
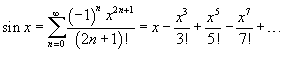
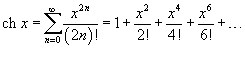
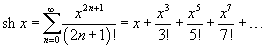
13. Т-ма Лейбница
Теорема формулируется следующим образом. Знакочередующийся ряд
![]() сходится, если
выполняются оба условия:
сходится, если
выполняются оба условия:
Из теоремы Лейбница вытекает следствие, позволяющее оценить погрешность вычисления неполной суммы ряда:
![]()
Остаток
сходящегося знакочередующегося
ряда ![]() будет
по модулю меньше первого отброшенного
слагаемого:
будет
по модулю меньше первого отброшенного
слагаемого:
![]()
ДОКАЗАТЕЛЬСТВО Допустим, что ряд начинается с положительного числа (в противном случае по приведённому ниже доказательству следует рассматривать сходимость ряда, начинающегося со второго члена).
2n-ая
частичная сумма данного ряда равна ![]() Так
как каждая сумма в скобках неположительна
и
Так
как каждая сумма в скобках неположительна
и ![]() то
отсюда следует ограниченность 2n-ой
частичной суммы сверху числом
то
отсюда следует ограниченность 2n-ой
частичной суммы сверху числом ![]()
Также
та же 2n-ая сумма равна ![]() Каждая
сумма в скобках неотрицательна. Отсюда
следует неубывание
последовательности
Каждая
сумма в скобках неотрицательна. Отсюда
следует неубывание
последовательности ![]() то
есть для любого
то
есть для любого ![]() выполняется
выполняется ![]()
Из
первого предложения доказательства
эта последовательность ограничена
сверху. Значит, существует такое число
s, что ![]()
Далее,
так как ![]() и
так как
и
так как ![]() то
то ![]() Сумма
данного ряда равна
Сумма
данного ряда равна ![]() где
где ![]() —
конечное число. Доказательство сходимости
завершено.
—
конечное число. Доказательство сходимости
завершено.
