Билет1

1.Граф, или неориентированный граф   — это упорядоченная пара  , для которой выполнены следующие условия:  — это непустое множество вершин или узлов,  — это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

В ершины и рёбра графа называются также элементами графа, число вершин в графе   — порядком, число рёбер   — размером графа. Дерево — это связный ациклический граф.^[1] Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути. Ориентированный граф (сокращённо орграф)   — это упорядоченная пара  , для которой выполнены следующие условия:  — это непустое множество вершин или узлов,  — это множество (упорядоченных) пар различных вершин, называемых дугами илиориентированными рёбрами. Дуга — это упорядоченная пара вершин  , где вершину   называют началом, а   — концом дуги. Можно сказать, что дуга   ведёт от вершины   к вершине  . Граф разреженный, если |E| << |V^2|

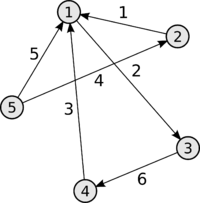
М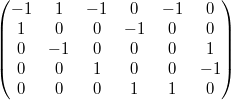 атрица смежности: Один из самых распространённых способов хранения графа - матрица смежности. Она представляет собой  двумерный массив. Если в клетке i, j (i – строка, j - столбец) установлено значение пусто (как правило, это очень большая величина или величина, которой заведомо не может равняться вес ребра), то дуги, начинающейся в вершине i и кончающейся в вершине j, нет. Иначе дуга есть. Если она есть, то в соответствующую ячейку записывают ее вес. Если граф не взвешенный, то вес дуги считается равным единице. Минус: много памяти (медленно работает и много памяти на разреженных графах)

Плюс: можно узнать за const есть ли ребро между 2 вершинами

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы соответствуют ребрам, строки — вершинам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В случае ориентированного графа каждому ребру <x,y> ставится в соответствие "-1" на позиции (x,y) и "1" на позиции (y,x); если связи между вершинами нет, то ставится в соответствие "0"

2.Алгоритм Рабина — Карпа — это алгоритм поиска строки, который ищет шаблон, то есть подстроку, в тексте, используяхеширование. Одно из простейших практических применений алгоритма Рабина — Карпа состоит в определении плагиата. Например, что студент пишет работу по Моби Дику. Коварный профессор находит различные исходные материалы по Моби Дику и автоматически извлекает список предложений в этих материалах. Затем, алгоритм Рабина — Карпа может быстро найти в проверяемой статье примеры вхождения некоторых предложений из исходных материалов. Для устранения чувствительности алгоритма к небольшим различиям, можно игнорировать детали, такие как регистр или пунктуация при помощи их удаления. Поскольку количество строк, которые мы ищем, k, очень большое, обычные алгоритмы поиска одиночных строк становятся неэффективными. Хэш-функция — это функция, которая преобразует каждую строку в числовое значение, называемое хэш-значение; например, мы можем иметь hash("hello")=5. Алгоритм использует тот факт, что если две строки одинаковы, то и их хэш-значения также одинаковы. Таким образом, всё что нам нужно, это посчитать хэш-значение той подстроки, которую мы ищем и затем найти подстроку с таким же хэш-значением.

Однако, существуют две проблемы связанные с этим. Первая, так как существует очень много различных строк, для того, чтобы иметь небольшие хэш-значения, мы должны иметь некоторые строки, хэш-значения которых совпадают. Это означает, что несмотря на то, что хэш значения совпадают, строки могут не совпадать; нам необходимо проверять что это действительно так, что занимает достаточно много времени для длинных подстрок. К удаче, хорошая хэш-функция обеспечивает нам то, что при достаточно хороших вводных значениях это не будет происходить очень часто, и в результате среднее время поиска мало.

Б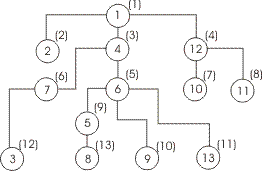 илет2

1.Поиск в ширину (breadth - first search) - один из базовых алгоритмов , лежащий в основе многих других алгоритмов для графов. Например, алгоритм Дейкстры для поиска кратчайших путей для заданной  вершины или алгоритм Примапоиска минимального покрывающего дерева являются обобщениями поиска в ширину.

Пусть задан граф G=(V, E) и начальная вершина s. Алгоритм поиска в ширину перечисляет все допустимые из s вершины в порядке возрастания расстояния от s. Расстоянием считается длина (число ребер) кратчайшего пути. В результате из графа выделяется часть, называемая "деревом поиска в ширину" с корнем s. В этом дереве путь из корняs в любую вершину будет одним из кратчайших путей из s в графе. Обход графа в ширину основывается на замене стека очередью. После такой модификации, чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди).

Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой непройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.

Алгоритм поиска в глубину

Пусть задан граф  , где   — множество вершин графа,   — множество ребер графа. Предположим, что в начальный момент времени все вершины графа окрашены в белый цвет. Выполним следующие действия:

И з множества всех белых вершин выберем любую вершину, обозначим её  .

Выполняем для неё процедуру DFS( ).

Повторяем шаги 1-3 до тех пор, пока множество белых вершин не пусто.

Процедура DFS (параметр — вершина  )

Перекрашиваем вершину   в черный цвет.

Для всякой вершины  , смежной с вершиной u и окрашенной в белый цвет, выполняем процедуру DFS(w).

2.Конечный автомат — абстрактный автомат без выходного потока, число возможных состояний которого конечно. Результат работы автомата определяется по его конечному состоянию.

Существуют различные варианты задания конечного автомата. Например, конечный автомат может быть задан с помощью пяти параметров:  , где:

Q — множество состояний автомата;

q₀ — начальное (стартовое) состояние автомата ()я ;

F — множество заключительных (или допускающих) состояний, таких что  ;

Σ — допустимый входной алфавит (конечное множество допустимых входных символов), из которого формируются строки, считываемые автоматом;

δ — заданное отображение множества   во множество   подмножеств Q:

(иногда δ называют функцией переходов автомата).

Автомат начинает работу в состоянии q₀, считывая по одному символу входной строки. Считанный символ переводит автомат в новое состояние из Q в соответствии с функцией переходов. Если по завершении считывания входного слова (цепочки символов) автомат оказывается в одном из допускающих состояний, то слово «принимается» автоматом. В этом случае говорят, что оно принадлежит языку данного автомата. В противном случае слово «отвергается».

Другие способы описания

Диаграмма состояний (или иногда граф переходов) — графическое представление множества состояний и функции переходов. Представляет собой нагруженный однонаправленный граф, вершины которого — состояния КА, ребра — переходы из одного состояния в другое, а нагрузка — символы, при которых осуществляется данный переход. Если переход из состояния q1 в q2 может быть осуществлен при появлении одного из нескольких символов, то над дугой диаграммы (ветвью графа) должны быть надписаны все они.

Таблица переходов — табличное представление функции δ. Обычно в такой таблице каждой строке соответствует одно состояние, а столбцу — один допустимый входной символ. В ячейке на пересечении строки и столбца записывается действие, которое должен выполнить автомат, если в ситуации, когда он находился в данном состоянии на входе он получил данный символ.

Алгоритм Бойера-Мура ( пример поиска подстрок )

1. Сканирование слева направо, сравнение справа налево. Совмещается начало текста (строки) и шаблона, проверка начинается с последнего символа шаблона. Если символы совпадают, производится сравнение предпоследнего символа шаблона и т. д. Если все символы шаблона совпали с наложенными символами строки, значит, подстрока найдена, и поиск окончен.

Если же какой-то символ шаблона не совпадает с соответствующим символом строки, шаблон сдвигается на несколько символов вправо, и проверка снова начинается с последнего символа.

Билет 3

1.Топологическая сортировка — упорядочивание вершин бесконтурного ориентированного графа согласно частичному порядку, заданному ребрами орграфа на множестве его вершин.

П усть дан бесконтурный ориентированный простой граф  . Через   обозначим множество вершин таких, что  . То есть,   — множество всех вершин, из которых есть дуга в вершину  . Пусть   — искомая последовательность вершин.

пока выбрать любую вершину такую, что и

удалить из всех

Н аличие хотя бы одного контура в графе приведёт к тому, что на определённой итерации цикла не удастся выбрать новую вершину  .

Для графа 

(Бесконтурный ориентированный граф)

существует несколько согласованных последовательностей его вершин, которые могут быть получены при помощи топологической сортировки, например: 1) 7,5,11,3,8,2,9,10 2) 3,7,5,8,11,10,9,2

Видно, что в последовательности могут быть переставлены любые две стоящие рядом вершины, которые не входят в отношение частичного порядка  .

При помощи топологической сортировки строится корректная последовательность выполнения действий, всякое из которых может зависеть от другого: последовательность прохождения учебных курсов студентами, установки программ при помощипакетного менеджера, сборки исходных текстов программ при помощи Makefile'ов.