
- •Часть 1. Измерения и измерительные приборы. Содержание
- •Лекция 1 Введение
- •1.1. Измерения и их классификация
- •1.2. Метрология, основные задачи.
- •1.3. Погрешности измерений
- •1.3.3 Общая погрешность измерения .
- •1.4. Виды измерений и общие требования к измерениям для артиллерийских испытаний
- •1.5. Оценка измеряемого параметра по ограниченному числу измерений
- •1.5.1 Точечная оценка измеряемого значения
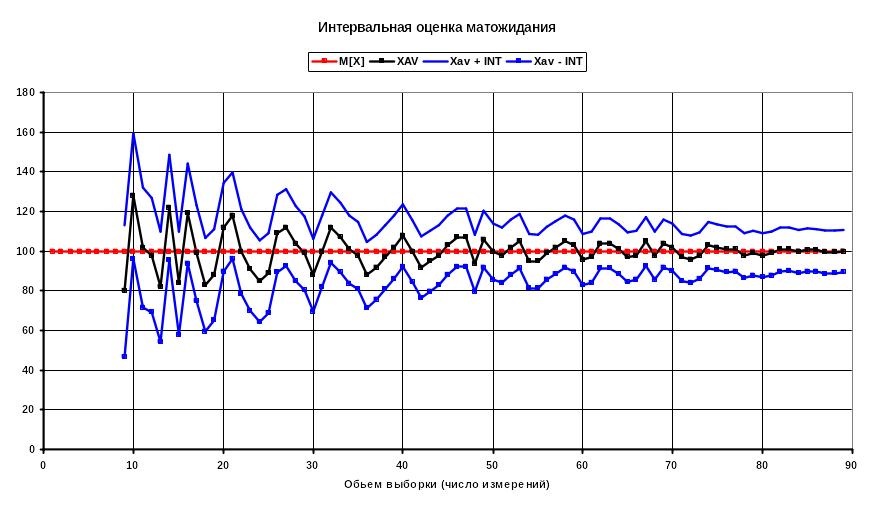
- •1.5.2 Интервальная оценка результатов измерений
- •Нормальный закон распределения вероятности в измерениях.
- •1.5.3. Обнаружение грубых погрешностей и их устранение.
- •1.5.4. Определение погрешностей для косвенных измерений.
- •1.6. Жизненный цикл техники (тс) и процесс эксплуатации техники (пэт).
- •1.6.1. Эксплуатация техники, основные показатели ее качества.
- •Показатели качества (применение к различным областям промышленности).
- •Себестоимость продукции
1.5.3. Обнаружение грубых погрешностей и их устранение.
Обнаружение грубых погрешностей решается методами проверки статистических гипотез. Проверяемая гипотеза состоит в том, что результат измерения Xk не содержит грубой погрешности. Сомнительным может быть только наибольший Xmax или наименьший Xmin из результатов. Для проверки гипотезы составим величины
![]() ;
;
![]() ; 1.17
; 1.17
При заданной доверительной вероятности (обычно, 0.1 или 0.05 ), или уровне значимости q = 1 - , можно найти те наибольшие значения , которое случайная величина может принимать по чисто случайным причинам. Величину можно найти по таблице Приложения 2.
Если выборка достаточно большая (N 30), то можно применить простой критерий Романовского выявления промахов, который часто используется на практике. Если для какого-то измеренного значения Xi выполняется неравенство:
|
Xi
-
![]() | > 3 , (1.18)
| > 3 , (1.18)
то это – промах. Этот критерий очень удобен для применения и автоматизации измерений.
Таким образом, порядок обработки результатов измерений состоит в следующем :
определяют точечные оценки истинного значения измеряемой величины и среднеквадратического отклонения результатов измерений,
проверяют нормальность распределения результатов измерения (или принятие этой гипотезы без обоснования),
задаваясь значениями доверительных вероятностей, находят доверительные границы результата измерений, и доверительный интервал для среднего квадратического отклонения измерений,
определяют наличие грубых погрешностей, и, если последние обнаружены, соответствующие результаты отбрасывают и повторяют вычисления.
1.5.4. Определение погрешностей для косвенных измерений.
Вычисления погрешностей, о которых говорилось выше, относятся к прямым измерениям. Однако наибольшее распространение в настоящее время имеют косвенные измерения. Особенно широко распространены эти измерения в артиллерийских испытаниях. Так, для стендовых испытаний и испытаний вне ствола, важно определить скорость снаряда, или отката ствола, которая вычисляется как отношение расстояния к времени пролета. Практически мы измеряем это расстояние между датчиками (с погрешностью), и время пролета ( с погрешностью). Таким образом, это – типично косвенное измерение.
Опишем процедуру получения погрешностей для косвенных измерений. Напомним, что при косвенных измерениях значение искомой величины получают на основании известной зависимости, связывающей с другими физическими величинами, которые измеряют прямыми измерениями.
Рассмотрим общий случай, когда требуется оценить истинное значение величины Z , которая связана с величинами Xm (m=1, . . .,n), которые измеряют прямыми методами. Величина Z связана с Xm (m=1, . . .,n) общим нелинейным соотношением:
Z = F (X1 , X2 , . . . , Xn ). (1.19)
Найдем
оценку матожидания
![]() результата косвенного измерения по
результатам матожиданий
результата косвенного измерения по
результатам матожиданий
![]() прямых измерений, при этом искомая
оценка должна иметь наименьшую дисперсию,
и следовательно, наибольшую точность
среди всех возможных оценок (быть
эффективной).
прямых измерений, при этом искомая
оценка должна иметь наименьшую дисперсию,
и следовательно, наибольшую точность
среди всех возможных оценок (быть
эффективной).
Считаем, что в процессе измерений величин Xm (m=1, . . .,n) систематические погрешности уже исключены, или пренебрежимо малы по сравнению со случайными погрешностями δm (m=1, . . .,n). Также считаем, что измерения величин Xm (m=1, . . .,n) являются независимыми (что обычно выполняется в практике измерений), поэтому сами случайные погрешности δm (m=1, . . .,n) тоже независимы друг от друга. Считая, что случайные погрешности малы ( |δm | < |Xm |), можно из (1.19) получить следующее разложение:
Z
= F
(![]() ) = F
(
) = F
(![]() )
+
)
+
![]() + . . . ; (1.20)
+ . . . ; (1.20)
В (1.20) отброшены члены второго и высших порядков по сравнению с случайными погрешностями. В качестве наиболее достоверной оценки матожидания косвенного измерения получаем из (1.20):
Z
= F
(![]() )
;
(1.21)
)
;
(1.21)
Введем частные погрешности косвенного измерения, которые определяют вклад погрешности измерения величины Xm в общую погрешность :
Em
=
![]() ;
;
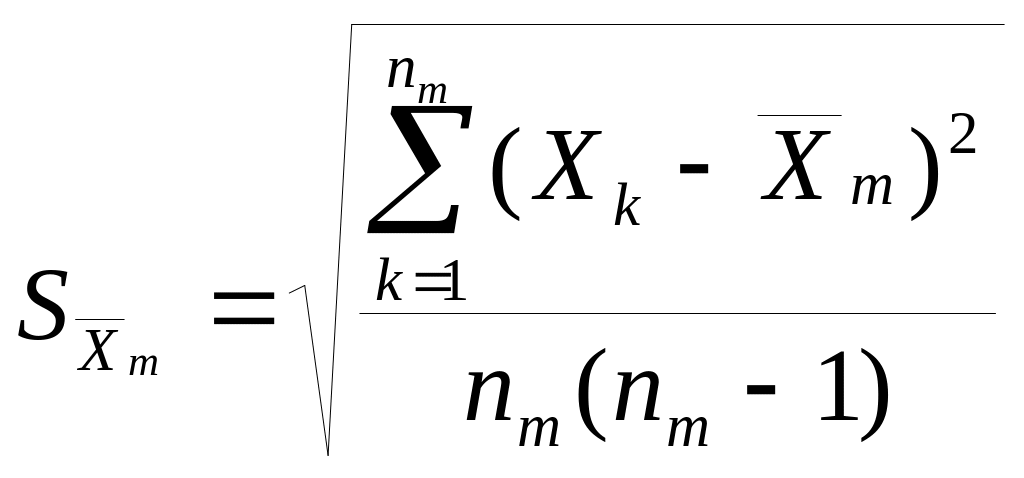 ; (1.22)
; (1.22)
Тогда общую дисперсию косвенного измерения можно оценить формулой:
![]() ;
(1.23)
;
(1.23)
Окончательный итог косвенного измерения (для заданной доверительной вероятности Р) записывается в виде:
Z
=
![]() ;
(1.24)
;
(1.24)
Здесь число степеней свободы для квантиля Стьюдента tP рассчитывается по формуле:
K
=
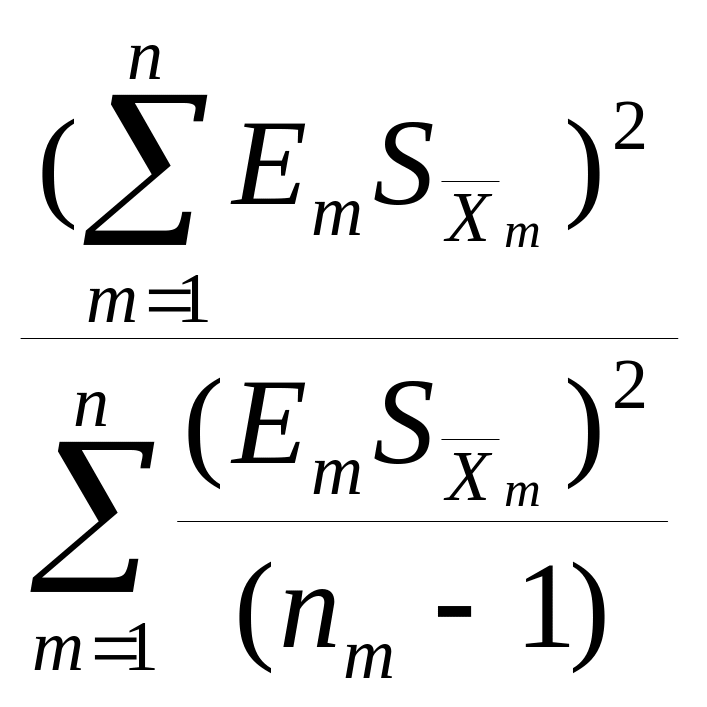 ;
(1.25)
;
(1.25)
Эффективное число степеней свободы К обычно получается дробным, поэтому для отыскания квантиля Стьюдента надо применить интерполяцию.
Существует общепринятый критерий ничтожных погрешностей, с помощью которого можно пренебречь некоторыми погрешностями. Частной погрешностью можно пренебречь, если для нее выполняется неравенство:
Em
<
![]() ;
(1.26)
;
(1.26)
ПРИМЕР ????
ПРИМЕР. Как мы говорили, при стендовых испытаний важно определить скорость отката ствола. Для этого на стенде устанавливаются несколько датчиков регистрации положения ствола, причем датчики устанавливаются на одинаковом расстоянии Н друг от друга. При этом измеряем разность времени Δt, за которое ствол проходит между двумя соседними датчиками. Таким образом, можно определить среднюю скорость отката ствола V в промежутке между двумя датчиками: V= H / Δt. Практически мы измеряем это расстояние между датчиками с погрешностью δH (обычно это составляет 1 – 5 мм), и время пролета ( с погрешностью δΔt , которая может составлять 10-4 – 10-6 с ). Таким образом, это – типично косвенное измерение, причем типовые значения – это Н ≈ 0.5м, а V0 ≈ 10 м/с , что приводит к типовой оценке для Δt ≈ 5*10-2 c.
В соответствие с (1.20) имеем:
ΔV = δH / Δt + H * δΔt ;
В
соответствие с нашими измерениями,
имеем
![]() = 0.4 m;
= 0.4 m;
![]() = 0.042 s;
δΔt
=
= 0.042 s;
δΔt
=
Дать данные измерений:
Н = 0.500, 0.501, 0.497, 0.499, 0.503, 0.498, 0.502, 0.500, 0.499, 0.498 м.
Δt = 0.042501, 0.042499, 0.042502, 0.042498, 0.0425, 0.042502, 0.0425, 0.042497, 0.042499, 0.042503 с.
Все остальное – вычислить по формулам (1.21) – (1.25) .
Приложение 1
Интервальная оценка математического ожидания результата измерения при неизвестной дисперсии.
Квантили распределения Стьюдента
Ν |
Уровни значимости, α |
||||||||
0,80 |
0,40 |
0,20 |
0,10 |
0,050 |
0,02 |
0,01 |
0,,005 |
0,,001 |
|
1 |
0,325 |
1,38 |
3,08 |
6,31 |
12,71 |
31,82 |
63,66 |
127,32 |
636,58 |
2 |
0,289 |
1,06 |
1,89 |
2,92 |
4,30 |
6,96 |
9,92 |
14,09 |
31,60 |
3 |
0,277 |
0,98 |
1,64 |
2,35 |
3,18 |
4,54 |
5,84 |
7,45 |
12,92 |
4 |
0,271 |
0,94 |
1,53 |
2,13 |
2,78 |
3,75 |
4,60 |
5,60 |
8,61 |
5 |
0,267 |
0,92 |
1,48 |
2,02 |
2,57 |
3,36 |
4,03 |
4,77 |
6,87 |
6 |
0,265 |
0,91 |
1,44 |
1,94 |
2,45 |
3,14 |
3,71 |
4,32 |
5,96 |
7 |
0,263 |
0,90 |
1,41 |
1,89 |
2,36 |
3,00 |
3,50 |
4,03 |
5,41 |
8 |
0,262 |
0,89 |
1,40 |
1,86 |
2,31 |
2,90 |
3,36 |
3,83 |
5,04 |
9 |
0,261 |
0,88 |
1,38 |
1,83 |
2,26 |
2,82 |
3,25 |
3,69 |
4,78 |
10 |
0,260 |
0,88 |
1,37 |
1,81 |
2,23 |
2,76 |
3,17 |
3,58 |
4,59 |
12 |
0,259 |
0,87 |
1,36 |
1,78 |
2,18 |
2,68 |
3,05 |
3,43 |
4,32 |
14 |
0,258 |
0,87 |
1,35 |
1,76 |
2,14 |
2,62 |
2,98 |
3,33 |
4,14 |
16 |
0,258 |
0,86 |
1,34 |
1,75 |
2,12 |
2,58 |
2,92 |
3,25 |
4,01 |
18 |
0,257 |
0,86 |
1,33 |
1,73 |
2,10 |
2,55 |
2,88 |
3,20 |
3,92 |
20 |
0,257 |
0,86 |
1,33 |
1,72 |
2,09 |
2,53 |
2,85 |
3,15 |
3,85 |
25 |
0,256 |
0,86 |
1,32 |
1,71 |
2,06 |
2,49 |
2,79 |
3,08 |
3,73 |
30 |
0,256 |
0,85 |
1,31 |
1,70 |
2,04 |
2,46 |
2,75 |
3,03 |
3,65 |
40 |
0,255 |
0,85 |
1,30 |
1,68 |
2,02 |
2,42 |
2,70 |
2,97 |
3,55 |
60 |
0,254 |
0,85 |
1,30 |
1,67 |
2,00 |
2,39 |
2,66 |
2,91 |
3,46 |
120 |
0,254 |
0,84 |
1,29 |
1,66 |
1,98 |
2,36 |
2,62 |
2,86 |
3,37 |
