1.5. Оценка измеряемого параметра по ограниченному числу измерений

1.5.1 Точечная оценка измеряемого значения

Обычно в ходе испытаний проверяется соответствие того или иного показателя качества заданным заказчиком требованиям. Считают, что система успешно прошла испытания, если ее параметры, полученные по результатам испытаний, будут не хуже заданных в тактико-технических требованиях (ТТТ). Из-за наличия систематических и случайных погрешностей измерений определить истинные значения параметров технической системы практически невозможно, поэтому в результате испытаний определяются не сами параметры, а их статистические оценки.

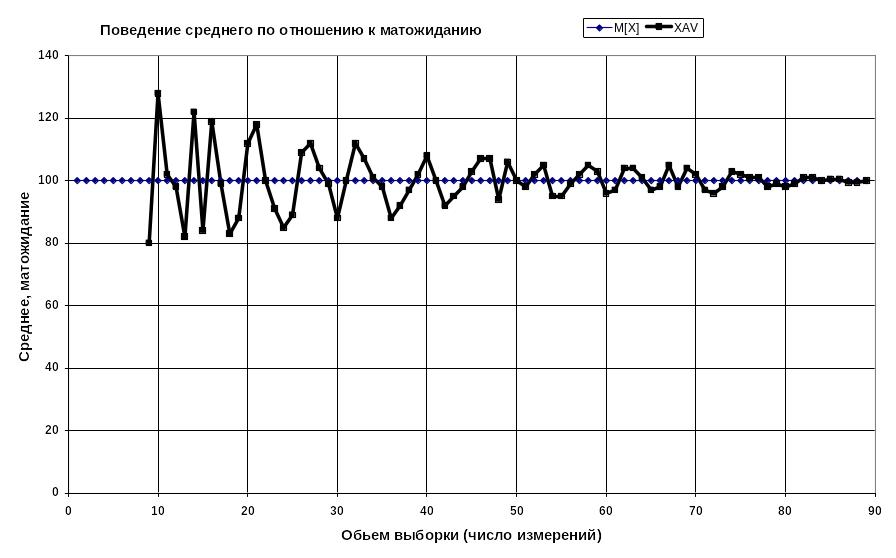
Такая оценка, называемая точечной, зависит от самого оцениваемого параметра Х, и от количества измерений (испытаний) N . К оценке предьявляется ряд требований, определяющих ее пригодность для применения [1,2]:

• состоятельность, (при увеличении числа измерений она приближается к точному значению Х ),

• несмещенность, (ее математическое ожидание равно оцениваемому параметру Х ),

• эффективность, (ее дисперсия меньше дисперсии любой другой оценки данного параметра).

Примером такой точечной статистической оценки математического ожидания измеряемого параметра Х, удовлетворяющей всем трем требованиям, служит среднее значение [1,2]:

, 1.2

где N – число измерений;

x_i – результат i-го измерения.

Точность таких оценок характеризуется близостью экспериментальных данных к действительным значениям параметра объекта.

В качестве точечной оценки среднеквадратического отклонения многократного измерения принимается величина S

. 1.3

Среднеквадратическое отклонение измерения, вычисленное по этой формуле, является смещенной оценкой, а несмещенной оценкой его является величина S

. 1.4

Само среднее значение тоже является случайной величиной, и его отклонение от истинного значения X характеризуется дисперсией S_x для среднего значения, которое вычисляется по формуле

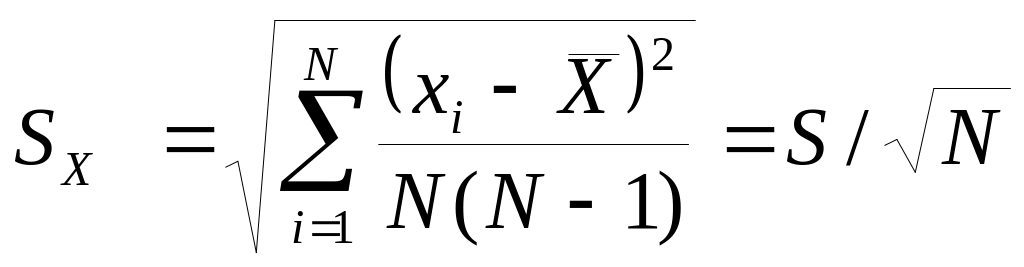. 1.5

Как видно из этой формулы, дисперсия среднего значения с ростом N убывает быстрее, чем  .

Полученные оценки позволяют сделать заключение о точности проведенных измерений. Результаты измерений записываются в виде X = ; S = . . . ; S_X =. . . . . ; N = . . . .

1.5.2 Интервальная оценка результатов измерений

При большом числе испытаний точечные оценки показателей будут приближаться к истинным значениям, но реально большое число испытаний произвести затруднительно. Поэтому в таком случае используют интервальные оценки, достоверность которых характеризуется доверительной вероятностью к результату измерения. Использование интервальных оценок позволяет связать показатели точности и достоверности с числом испытаний.

Для установления такой связи необходимо определить точное распределение выборочной характеристики (статистической оценки) на основе вида закона распределения генеральной совокупности (результата измерения). Поэтому в процессе получения интервальных оценок измерения последовательно решаются четыре задачи:

• проверка соответствия результатов измерения нормальному закону распределения (или его принятие)

• вычисление доверительных границ для матожидания результата измерения

• вычисление доверительных интервалов для среднеквадратического отклонения результата измерения

• обнаружение грубых погрешностей (промахов).