Нормальный закон распределения вероятности в измерениях.

В процессе эксплуатационных наблюдений на результат измерения параметра Х системы влияет большое число различных по своей природе факторов. Это приводит к вероятностному характеру измеряемой величины. При этом принимают гипотезу о нормальном законе распределения результатов измерений параметра. Широкое распространение нормального распределения погрешностей в практике измерений обьясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которых принимали участие многие математики – Муавр, Лаплас, Гаусс, П.Л. Чебышев, А.М. Ляпунов.

Центральная предельная теорема говорит о том, что распределение случайных погрешностей будет близко к нормальному закону, когда результаты измерения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Именно поэтому, в измерениях, обычно принимают гипотезу о нормальном распределении погрешностей измерения.

То-есть, измеряемый параметр X имеет нормальное распределение cо средним (математическим ожиданием) и дисперсией σ²:

. 1.6

Очевидно, по мере увеличения дисперсии (среднеквадратического отклонения измерения) распределение f(x) расплывается. Это приводит к тому, что вероятность появления больших значений погрешностей возрастает, а вероятность появления меньших погрешностей – уменьшается, т.е., увеличивается рассеивание результатов измерения.

Гауссова функция имеет вид колокола, причем максимум функции достигается в точке , и сам максимум равен . В практике, вместо  следует применять оценку S*.

Нормальный закон распределения плотности вероятности соответствует интегральной функции распределения Лапласа вида:

F(x) = P( X < x) = 1.7

Она показывает вероятность того, что случайная величина не превосходит значения х . Ее значения табулированы в таблице (в зависимости от  и Р).

Проверять гипотезу о нормальном распределении результатов эксплуатационных наблюдений необходимо в ответственных случаях. Проверка может быть проведена несколькими способами. Мы будем применять наиболее простой способ проверки [2].

1. По результатам эксплуатационных измерений (выборки) вычислим третий ₃ и четвертый ₄ статистический моменты опытного распределения вероятности:

. 1.8

. 1.9

и коэффициенты ассиметрии g₁ и эксцесса g₂ опытного распределения

, . 1.10

2. Определяем средние квадратичные отклонения коэффициентов ассиметрии и эксцесса:

; . 1.11

3. Проводим сравнение полученных величин.

Если выполняются одновременно неравенства:

| g₁ |  1.5 S₁ ; | g₂ + 6 / (N + 1)|  1.5 S₂ 1.12

то опытные данные подчиняются нормальному распределению.

Если же выполняется хотя бы одно из неравенств:

| g₁ |  3 S₁ ; | g₂ + 6 / (N + 1)|  2 S₂ 1.13

то опытные данные не подчиняются нормальному распределению.

В любом другом случае нельзя дать определенного ответа без дополнительного исследования.

Интервальная оценка математического ожидания измеряемой величины.

Интервальные оценки находятся в виде интервала, который накрывает истинное значение оцениваемой величины с доверительной вероятностью р. Смысл оценки параметра с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенной вероятностью (доверительной) р находятся истинные значения оцениваемого параметра. Половина доверительного интервала называется доверительной границей  случайного отклонения результатов измерения, соответствующих доверительной вероятности р (для их расчета принимается доверительная вероятность (1+ р) / 2).

Как правило, при обработке результатов измерения решается задача нахождения интервальной оценки математического ожидания измеряемого параметра при неизвестной дисперсии.

За основу интервальных оценок берутся точечные оценки –

выборочное среднее и выборочная дисперсия измерения:

, . 1.14

Интервальная оценка математического ожидания при

неизвестной дисперсии измерения вычисляется следующим образом. При нормальном распределении генеральной совокупности величина имеет распределение Стьюдента с (N-1) степенями свободы. Таким образом, интервальная оценка математического ожидания запишется в виде:

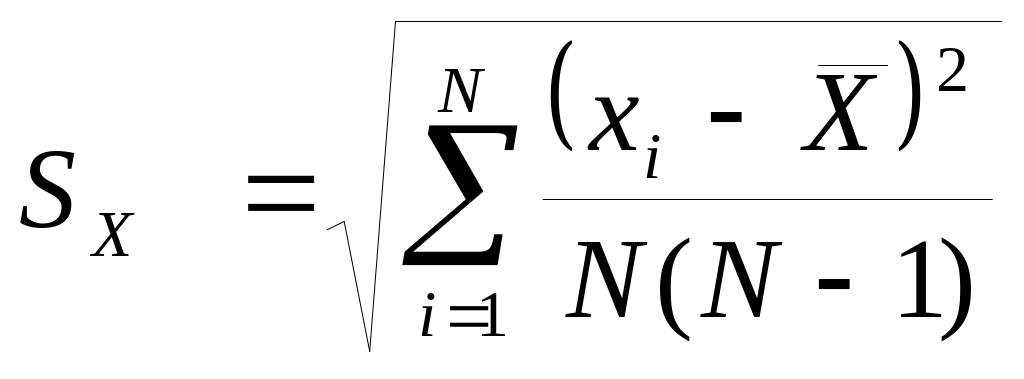. 1.15

Здесь величина  - это уровень значимости, который связан с заданной доверительной вероятностью р следующим образом .

Значения квантилей распределения Стьюдента приведены в Приложении 1.

Результаты измерений записываются в виде:

X = ; P = . . . . . , 1.16

Здесь  = S_X t_1-/2 .

Таким образом, в результате измерения получаем “полосу значений измеряемой величины с несколько расплывчатыми границами”. Истинное значение лежит внутри этих границ, и необязательно, чтобы оно лежало в середине интервала. При этом, вероятность нахождения результата измерения внутри интервала не стопроцентная, а несколько меньшая. Следовательно, нахождение результата измерения вне границ не исключено, хотя и может быть маловероятным.

Пример 1. Число степеней равно 14, и принимаем р = 0.95. Тогда = 2.62, S_X = 1.583; и

X= 798.8  4 мм; P = 95% .