15. Расчетная длина нп, течение н за перевальной точкой.

При гидравлическом, расчете, как правило, сочетают аналитические выкладки с графическими построениями. Прежде чем рассчитать число насосных станций, необходимо определить гидравлические уклоны в одиночной трубе i₀ и лупинге i_Л (вставке i_B). Затем исследуют профиль трассы для определения перевальной точки и расчетной длины трубопровода. Для этого на сжатом профиле в соответствии с принятыми на нем масштабами длин и высот строят прямоугольные треугольники, изображающие, например, падение напора на участке трубопровода длиной 100 км (рис. 16, а). Вертикально вверх от какой-нибудь точки с (в стороне от профиля или на нем) в масштабе высот строят отрезок сb, равный по величине напору, теряемому на преодоление сопротивления в трубе длиной 100 км; по горизонтали, вправо от точки с, в масштабе длин откладывают отрезок са, равный по величине 100 км; соединяя точки а и b прямой, получают треугольник bас, характеризующий гидравлический уклон. Затем параллельно гипотенузе этого треугольника проводят касательные к вершинам линии профиля. Если какая-нибудь из касательных не пересекает нигде в другом месте профиль, то соответствующая вершина π является перевальной точкой. Как видно из рис. 16, а, перевальная точка не обязательно является наивысшей точкой трассы. Расстояние от перевальной точки до начальной точки/трубопровода называется расчетной длиной.

М ожно доказать, что достаточно закачать жидкость на перевальную точку, чтобы она с тем же расходом самотеком достигла конца трубопровода. Из рис. 16, б видно, что располагаемый напор, равный разности z_π — z₂, больше напора, необходимого для преодоления сопротивления на участке от перевальной точки до конца трубопровода:

Таким образом, самотек жидкости за перевальной точкой обеспечен.

Рассмотрим движение жидкости за перевальной точкой. В промежутке трассы от перевальной точки до конечного пункта выделим два участка: ππ₁ длиной l₁ и π₁κ длиной l₂ (рис. 16, б). На последнем из них самотечное движение жидкости обеспечивается разностью высот точек π₁ и к (il₂ = ∆z). На участке ππ₁, как видно из чертежа, ∆z_π_-_π₁ > il₁ на величину πс. Но это противоречит условию баланса потерянного (il₁) и активного (∆z_π_-π1) напоров. Следовательно, на участке ππ₁ гидравлический уклон должен быть больше i. Это возможно только в случае увеличения скорости движения жидкости на участке ππ₁. Из уравнения сплошности: видно, что с увеличением скорости живое сечение потока Р должно уменьшаться. Следовательно, за перевальной точкой (до пункта π₁) жидкость движется при частичном заполнении поперечного сечения трубопровода. Давление на этом участке равно давлению насыщенного пара перекачиваемой жидкости.

16. Расчет нефтепровода с лупингами и вставками.

Гидравлический уклон представляет собой потерю напора на трение, отнесенную к единице длины трубопровода: или по Лейбензону

Отложим от начальной и конечной точек на профиле трассы трубопровода напоры Н₁ = р₁/ρg и Н₂ = р₂/ρg (рис. 12) и концы полученных отрезков соединим прямой. Эта прямая называется линией падения напора или линией гидравлического уклона. Она показывает распределение напора по длине трубопровода.

Аналитическое выражение линии гидравлического уклона имеет вид Н = Н₁—il.

Тангенс угла наклона этой прямой (i) называется гидравлическим уклоном (геометрическое определение).

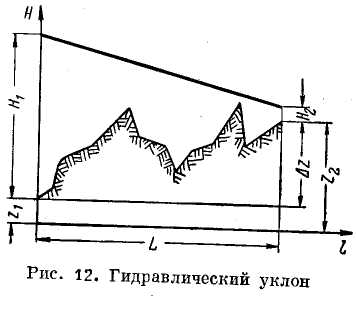
Из чертежа видно, что где Н_г — Н₂ — Аг = h — потери напора.

Если на каком-либо участке трассы проложен параллельный трубопровод (лупинг) или трубопровод другого диаметра (вставка), гидравлический уклон на нем будет отличаться от гидравлического уклона магистрали. Найдем соотношение между гидравлическим уклоном лупинга (вставки) и магистрали. Будем считать, что режим движения нефти в них одинаков.

Пользуясь обозначениями рис. 13, имеем: гидравлический уклон магистрали